travelling salesman problem solve

• Google OR-Tools
• Español – América Latina
• Português – Brasil
• Tiếng Việt

Traveling Salesperson Problem

This section presents an example that shows how to solve the Traveling Salesperson Problem (TSP) for the locations shown on the map below.

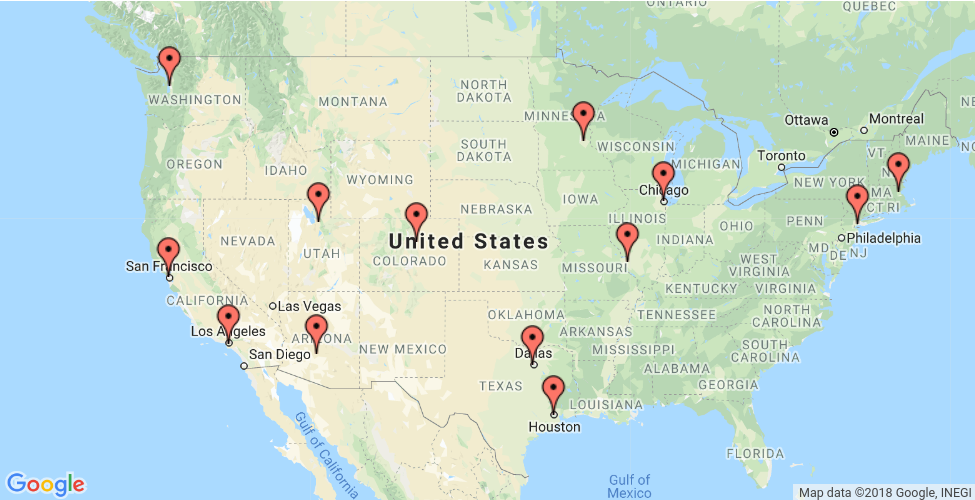
The following sections present programs in Python, C++, Java, and C# that solve the TSP using OR-Tools

Create the data

The code below creates the data for the problem.

The distance matrix is an array whose i , j entry is the distance from location i to location j in miles, where the array indices correspond to the locations in the following order:

The data also includes:

• The number of vehicles in the problem, which is 1 because this is a TSP. (For a vehicle routing problem (VRP), the number of vehicles can be greater than 1.)
• The depot : the start and end location for the route. In this case, the depot is 0, which corresponds to New York.

Other ways to create the distance matrix

In this example, the distance matrix is explicitly defined in the program. It's also possible to use a function to calculate distances between locations: for example, the Euclidean formula for the distance between points in the plane. However, it's still more efficient to pre-compute all the distances between locations and store them in a matrix, rather than compute them at run time. See Example: drilling a circuit board for an example that creates the distance matrix this way.

Another alternative is to use the Google Maps Distance Matrix API to dynamically create a distance (or travel time) matrix for a routing problem.

Create the routing model

The following code in the main section of the programs creates the index manager ( manager ) and the routing model ( routing ). The method manager.IndexToNode converts the solver's internal indices (which you can safely ignore) to the numbers for locations. Location numbers correspond to the indices for the distance matrix.

The inputs to RoutingIndexManager are:

• The number of rows of the distance matrix, which is the number of locations (including the depot).
• The number of vehicles in the problem.
• The node corresponding to the depot.

Create the distance callback

To use the routing solver, you need to create a distance (or transit) callback : a function that takes any pair of locations and returns the distance between them. The easiest way to do this is using the distance matrix.

The following function creates the callback and registers it with the solver as transit_callback_index .

The callback accepts two indices, from_index and to_index , and returns the corresponding entry of the distance matrix.

Set the cost of travel

The arc cost evaluator tells the solver how to calculate the cost of travel between any two locations — in other words, the cost of the edge (or arc) joining them in the graph for the problem. The following code sets the arc cost evaluator.

In this example, the arc cost evaluator is the transit_callback_index , which is the solver's internal reference to the distance callback. This means that the cost of travel between any two locations is just the distance between them. However, in general the costs can involve other factors as well.

You can also define multiple arc cost evaluators that depend on which vehicle is traveling between locations, using the method routing.SetArcCostEvaluatorOfVehicle() . For example, if the vehicles have different speeds, you could define the cost of travel between locations to be the distance divided by the vehicle's speed — in other words, the travel time.

Set search parameters

The following code sets the default search parameters and a heuristic method for finding the first solution:

The code sets the first solution strategy to PATH_CHEAPEST_ARC , which creates an initial route for the solver by repeatedly adding edges with the least weight that don't lead to a previously visited node (other than the depot). For other options, see First solution strategy .

Add the solution printer

The function that displays the solution returned by the solver is shown below. The function extracts the route from the solution and prints it to the console.

The function displays the optimal route and its distance, which is given by ObjectiveValue() .

Solve and print the solution

Finally, you can call the solver and print the solution:

This returns the solution and displays the optimal route.

Run the programs

When you run the programs, they display the following output.

In this example, there's only one route because it's a TSP. But in more general vehicle routing problems, the solution contains multiple routes.

Save routes to a list or array

As an alternative to printing the solution directly, you can save the route (or routes, for a VRP) to a list or array. This has the advantage of making the routes available in case you want to do something with them later. For example, you could run the program several times with different parameters and save the routes in the returned solutions to a file for comparison.

The following functions save the routes in the solution to any VRP (possibly with multiple vehicles) as a list (Python) or an array (C++).

You can use these functions to get the routes in any of the VRP examples in the Routing section.

The following code displays the routes.

For the current example, this code returns the following route:

As an exercise, modify the code above to format the output the same way as the solution printer for the program.

Complete programs

The complete TSP programs are shown below.

Example: drilling a circuit board

The next example involves drilling holes in a circuit board with an automated drill. The problem is to find the shortest route for the drill to take on the board in order to drill all of the required holes. The example is taken from TSPLIB, a library of TSP problems.

Here's scatter chart of the locations for the holes:

The following sections present programs that find a good solution to the circuit board problem, using the solver's default search parameters. After that, we'll show how to find a better solution by changing the search strategy .

The data for the problem consist of 280 points in the plane, shown in the scatter chart above. The program creates the data in an array of ordered pairs corresponding to the points in the plane, as shown below.

Compute the distance matrix

The function below computes the Euclidean distance between any two points in the data and stores it in an array. Because the routing solver works over the integers, the function rounds the computed distances to integers. Rounding doesn't affect the solution in this example, but might in other cases. See Scaling the distance matrix for a way to avoid possible rounding issues.

Add the distance callback

The code that creates the distance callback is almost the same as in the previous example. However, in this case the program calls the function that computes the distance matrix before adding the callback.

Solution printer

The following function prints the solution to the console. To keep the output more compact, the function displays just the indices of the locations in the route.

Main function

The main function is essentially the same as the one in the previous example , but also includes a call to the function that creates the distance matrix.

Running the program

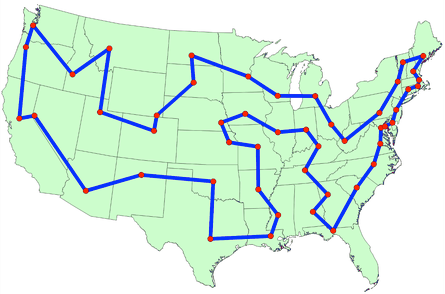
The complete programs are shown in the next section . When you run the program, it displays the following route:

Here's a graph of the corresponding route:

The OR-Tools library finds the above tour very quickly: in less than a second on a typical computer. The total length of the above tour is 2790.

Here are the complete programs for the circuit board example.

Changing the search strategy

The routing solver does not always return the optimal solution to a TSP, because routing problems are computationally intractable. For instance, the solution returned in the previous example is not the optimal route.

To find a better solution, you can use a more advanced search strategy, called guided local search , which enables the solver to escape a local minimum — a solution that is shorter than all nearby routes, but which is not the global minimum. After moving away from the local minimum, the solver continues the search.

The examples below show how to set a guided local search for the circuit board example.

For other local search strategies, see Local search options .

The examples above also enable logging for the search. While logging isn't required, it can be useful for debugging.

When you run the program after making the changes shown above, you get the following solution, which is shorter than the solution shown in the previous section .

For more search options, see Routing Options .

The best algorithms can now routinely solve TSP instances with tens of thousands of nodes. (The record at the time of writing is the pla85900 instance in TSPLIB, a VLSI application with 85,900 nodes. For certain instances with millions of nodes, solutions have been found guaranteed to be within 1% of an optimal tour.)

Scaling the distance matrix

Since the routing solver works over the integers, if your distance matrix has non-integer entries, you have to round the distances to integers. If some distances are small, rounding can affect the solution.

To avoid any issue with rounding, you can scale the distance matrix: multiply all entries of the matrix by a large number — say 100. This multiplies the length of any route by a factor of 100, but it doesn't change the solution. The advantage is that now when you round the matrix entries, the rounding amount (which is at most 0.5), is very small compared to the distances, so it won't affect the solution significantly.

If you scale the distance matrix, you also need to change the solution printer to divide the scaled route lengths by the scaling factor, so that it displays the unscaled distances of the routes.

Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.

Last updated 2023-01-16 UTC.

Learning center series

Travelling salesman problem explained

• Published on April 26, 2024
• by Oguzhan Uyar
• Last updated: 2 months ago

Revolutionize your understanding of the Travelling Salesman Problem (TSP); a mind-boggling conundrum that has compelled academia and industry alike. In the upcoming lines, we decode the key concepts, algorithms, and anticipated solutions for 2024 to this age-old dilemma.

Now, picture the TSP as a globetrotting traveling salesman who’s whirlwind journey. He must stop at every city once, only the origin city once, and find the quickest shortest possible route back home. If daunting to visualize, consider this: the possible number of routes in the problem concerning just 20 cities exceeds the number of atoms in the observable universe.

Fathom the sheer magnitude?

So, what is the Travelling Salesman Problem, and why has it remained unsolved for years? Let’s snap together the puzzle of this notorious problem that spans mathematics, computer science, and beyond. Welcome to an insightful voyage into the astonishing world of the TSP. Delve deeper into how optimizing travel routes can transform the efficiency of solving the Travelling Salesman Problem, marking a milestone in the journey toward more effective logistics and navigational strategies.

Understanding the Travelling Salesman Problem (TSP): Key Concepts and Algorithms

Defining the travelling salesman problem: a comprehensive overview.

The Travelling Salesman Problem, often abbreviated as TSP, has a strong footing in the realm of computer science. To the untrained eye, it presents itself as a puzzle: a salesperson or traveling salesman must traverse through a number of specific cities before an ending point and return to their ending point as of origin, managing to do so in the shortest possible distance. But this problem is not simply a conundrum for those fond of riddles; it holds immense significance in the broad field of computer science and optimization. Optimizing travel routes is the key to solving the Travelling Salesman Problem efficiently, ensuring the shortest and most cost-effective journey for salespeople or travelers.

The sheer computational complexity of TSP is what sets it apart, and incidentally, why it is considered a challenging problem to solve. Its complexity derives from the factorial nature of the problem: whenever a new city is added, the total number of possibilities increases exponentially. Thus, as the problem scope enlarges, it swiftly becomes computationally prohibitive to simply calculate all possible solutions to identify an optimal shortest route through. Consequently, developing effective and efficient algorithms to solve the TSP has become a priority in the world of computational complexity.

Polynomial Time Solution: The TSP can be solved by a deterministic Turing machine in polynomial time, which means that the number of steps to solve the problem can be at most 1.5 times the optimal global solution.

One such algorithm is the dynamic programming approach that can solve TSP problems in polynomial time. The approach uses a recursive formula to compute the shortest possible route that visits all other nodes in the cities exactly once and ends at all nodes in the starting point or city. Moreover, linear programming and approximation algorithms have also been used to find near-optimal solutions. Discover how dynamic programming and other strategies serve as algorithms for optimizing routes , enhancing efficiency in plotting course paths.

Unraveling TSP Algorithms: From Brute Force to Heuristics

A multitude of algorithms have been developed to contend with the TSP. The brute force method, for example, entails considering the shortest distance for all possible permutations of cities, calculating the total distance for six cities along each route, and selecting the shortest distance for one. While brute force promises an optimal solution, it suffers from exponential computational complexity, rendering it unfeasible for large datasets.

TSP Complexity: A TSP with just 10 cities has 362,880 possible routes , making brute force infeasible for larger instances.

On the other hand, we have heuristic algorithms that generate good, albeit non-optimal, solutions in reasonable timeframes. The greedy algorithm, for instance, initiates from a starting city and looks for the shortest distance from other nodes to the next node minimizes the distance, and guarantees speed but is not necessarily an optimal solution.

Algorithmic Potential: Local Solutions 4/3 Times Optimal Global: The theoretical conjecture suggests an algorithm that can provide a local solution within 4/3 times the optimal global solution.

Record Local TSP Solution: The record for a local solution to the Traveling Salesman Problem (TSP) is 1.4 times the optimal global solution, achieved in September 2012 by Andr´as Seb˝o and Jens Vygen.

Exploring further, we encounter more refined heuristic solutions such as the genetic algorithm and simulated annealing algorithm. These algorithms deploy probabilistic rules, with the former incorporating principles of natural evolution and the latter being inspired by the cooling process in metallurgy. They differ significantly from each other in terms of how they search for solutions, but when compared to brute force, they often offer a promising trade-off between quality and computational effort.

Certainly, the TSP is far more than a problem to puzzle over during a Sunday afternoon tea. It’s a complex computational task with real-world implications, and unraveling it requires more than brute force; it demands the application of sophisticated algorithms designed to balance efficiency and quality of results. Nevertheless, with a better understanding of the problem statement and its dynamics, you can unlock the potential to not just solve problems faster, but to do so more intelligently.

Save 80% of the time from managing deliveries and drivers.

Metrobi provides a dedicated operations manager that coordinates drivers on your behalf and solves urgent issues.

Practical Solutions to the Travelling Salesman Problem

Implementing tsp solutions: a step-by-step guide, a comprehensive process for implementing tsp solutions.

Developing complete, practical solutions for the Travelling Salesman Problem (TSP) requires a good grasp of specific algorithms. Visual aids, for example, such as finding all the edges leading out of a given city, can help to simplify the process. Enhance your ability to solve the Travelling Salesman Problem by mastering route optimization with Google Maps , streamlining your path and saving significant time on the go.

TSP's Computer Science Quest for Shortest Routes: The TSP involves finding the shortest route to visit a set of cities exactly once before returning to the starting city, aiming to minimize travel distance.

One popular approach to TSP problem solving is the dynamic programming approach, which involves breaking down the problem into smaller sub-problems and recursively solving them. Other approaches include approximation algorithms, which generate near-optimal solutions to small problems in polynomial time, and bound algorithms, which aim to find an upper bound on the optimal solution given graph top. Discover how software for planning routes can revolutionize your approach to the TSP problem, offering near-optimal solutions that enhance efficiency and effectiveness in logistical planning.

TSP Variants: ASTP and STSP The TSP can be divided into two types: the asymmetric traveling salesman problem (ASTP) and the symmetric traveling salesman problem (STSP)

Practical code implementation

Before diving into code manipulations, it’s worth noting that practical implementation varies based on the specifics of the problem and the chosen algorithm. Let’s further deconstruct these notions by examining the steps for code implementation for a pre-determined shortest path first. It’s crucial to efficiently concede each point of the shortest path, call other nodes, connect each node, and conclude each route. Hereby, I shall delve into the practicalities of coding from an output standpoint, concentrating on readability, scalability, and execution efficiency. Uncover how optimizing routes can elevate your coding practices for more efficient, scalable, and readable solutions in logistics and transportation.

TSP Instance Size: The size of the TSP instances used in the studies is 100 nodes.

Cluster Quantity in TSP Instances: The number of clusters in the TSP instances used in the studies is 10 .

The Quantity of Instances per Cluster in Studies: The number of instances in each cluster used in the studies is 100.

Optimizing TSP Solutions: Tips and Tricks

Tsp solutions optimization techniques.

An optimized solution for the TSP is often accomplished using advanced algorithms and techniques. Optimization techniques allow professionals to solve more intricate problems, rendering them invaluable tools when handling large datasets and attempting to achieve the best possible solution. Several approaches can be taken, such as heuristic and metaheuristic approaches, that can provide near-optimal solutions with less use of resources. Discover the key to enhancing your logistics operations by mastering the art of optimizing delivery routes , thereby achieving efficiency and reducing costs significantly.

Expert Advice for Maximum Efficiency Minimum Cost

Even the most proficient problem solvers can gain from learning expert tips and tricks. These nuggets of wisdom often provide the breakthrough needed to turn a good solution into a great one. The TSP is no exception. Peering into the realm of experts can provide novel and creative ways to save time, increase computation speed, manage datasets, and achieve the most efficient shortest route around.

By comprehending and implementing these solutions to the Travelling Salesman Problem, one can unravel the complex web of nodes and paths. This equips any problem-solver with invaluable insights that make navigating through real-world TSP applications much more manageable. By adopting sophisticated routing planner software , businesses can significantly streamline their delivery operations, ensuring a more predictable and cost-effective way of dealing with the challenges presented by the Travelling Salesman Problem.

Real-World Applications of the Travelling Salesman Problem

Tsp in logistics and supply chain management.

The Travelling Salesman Problem (TSP) is not confined to theoretical mathematics or theoretical computer science either, it shines in real-world applications too. One of its most potent applications resides in the field of logistics and supply chain management. Explore how the latest gratis route planning applications can revolutionize logistics and supply chain efficiency by uncovering the top 10 free software tools for 2024.

With globalization, the importance of more efficient routes for logistics and supply chain operations has risen dramatically. Optimizing routes and decreasing costs hold the key to success in this arena. Here’s where TSP comes into play. Discover how Planning for Multiple Stops can revolutionize your logistics, ensuring the most efficient paths are taken. Dive into our post to see how it streamlines operations and reduces expenses.

In the vast complexity of supply chain networks, routing can be a colossal task. TSP algorithms bring clarity to the chaos, eliminating redundant paths and pointing to the optimal route covering the most distance, shortest path, and least distance between all the necessary points—leading to a drastic dip in transportation costs and delivery times. Uncover how optimizing delivery routes can revolutionize your logistics, ensuring efficiency and cost-effectiveness in your delivery operations.

Real-World Examples

Consider the case of UPS – the multinational package delivery company. They’ve reportedly saved hundreds of millions of dollars yearly by implementing route optimization algorithms originating from the Travelling Salesman Problem. The solution, named ORION, helped UPS reduce the distance driven by their drivers roughly by 100 million miles annually. Understand the intricacies of the problem of routing vehicles to appreciate how businesses like UPS can significantly benefit from efficient logistical strategies and route optimization systems.

TSP in GIS and Urban Planning: Optimal Route

TSP’s contributions to cities aren’t confined to logistics; it is invaluable in Geographic Information Systems (GIS) and urban planning as well. A city’s efficiency revolves around transportation. The better the transport networks and systems, the higher the city’s productivity. And as city authorities continuously strive to upgrade transportation systems, they find an ally in TSP. Discover how TSP enhances road architecture by integrating specialized truck routing solutions , elevating urban transport strategies.

Advanced GIS systems apply TSP to design more efficient routes and routing systems for public transportation. The aim of the route is to reach maximum locations with the least travel time and least distance, ensuring essential amenities are accessible to everyone in the city. Discover how dynamic routing optimization can enhance city-wide transportation efficiency and accessibility for all residents.

The city of Singapore, known for its efficient public transportation system, owes part of its success to similar routing algorithms. The Land Transport Authority uses TSP-related solutions to plan bus routes, reducing travel durations and enhancing accessibility across the city.

Delving Deeper: The Complexity and History of the Travelling Salesman Problem

Understanding the complexity of tsp.

TSP is fascinating not just for its inherent practicality but also for the complexity it brings along. TSP belongs to a class of problems known as NP-hard, a category that houses some of the most complex problems in computer science. But what makes TSP so gnarled?

Unravel the Intricacies: Why is TSP complex?

TSP is a combinatorial optimization problem, which simply means that it’s all about figuring out the most often optimal solution among a vast number of possible solutions or combinations of approximate solutions. The real challenge comes from an innocent-sounding feature of TSP: As the number of cities (we call them nodes) increases, the complexity heightens exponentially, not linearly. The number of possible routes takes a dramatic upward turn as you add more nodes, clearly exemplifying why TSP is no walk-in-the-park problem. Discover how leveraging multi-stop itinerary planning can transform this complex task, offering a streamlined solution to navigate through the myriad of possibilities efficiently.

NP-hard and TSP: A Connection Explored

In computer science, we use the terms P and NP for classifying problems. P stands for problems where a solution can be found in ‘polynomial time’. NP stands for ‘nondeterministic polynomial time’, which includes problems where a solution can be verified in polynomial time. The concept of ‘NP-hardness’ applies to TSP. Any problem that can be ‘reduced’ to an NP problem in polynomial time is described as NP-hard. In simpler terms, it’s harder than the hardest problems of NP. TSP holds a famed position in this class, making it a noteworthy example of an NP-hard problem. Discovering efficient solutions for the Traveling Salesman Problem (TSP) exemplifies how optimizing routes can streamline complex logistical challenges, showcasing the practical impact of advancements in algorithmic route optimization.

A Look Back: The History of the Travelling Salesman Problem

TSP is not a new kid on the block. Its roots can be traced back to the 1800s, and the journey since then has been nothing short of a compelling tale of mathematical and computational advancements.

The Origins and Evolution of TSP

Believe it or not, the Travelling Salesman Problem was first formulated as a mathematical problem in the 1800s. This was way before the advent of modern computers. Mathematicians and logisticians were intrigued by the problem and its implications. However, it wasn’t until the mid-20th century that the problem started to gain more widespread attention. Over the years, the TSP has transformed from a theoretical model to a practical problem that helps solve real-world issues.

A Classic Shortest Route Problem Since 1930s: The TSP is a classic optimization problem within the field of operations research, first studied during the 1930s.

Milestones in TSP Research

Looking at all the cities and milestones in TSP research, the story is truly impressive. From some of the initial heuristic algorithms to solve smaller instances of TSP, to geometric methods and then approximation algorithms, TSP research has seen a lot. More recently, we have also seen practical solutions to TSP using quantum computing — a testament to how far we’ve come. Each of these milestones signifies an innovative shift in how we understand and solve TSP. Discovering the top delivery route planning software in 2024, we navigated through the advancements in TSP solutions to identify which applications excel in streamlining delivery logistics.

Wrapping Up The Journey With Algorithms and Solutions

The Travelling Salesman Problem (TSP) remains a complex enigma of business logistics, yet, the advent of sophisticated algorithms and innovative solutions are paving avenues to optimize routing, reduce travel costs further, and enhance customer interactions.

Navigating the TSP intricacies is no longer a daunting challenge but a worthwhile investment in refining operational efficiency and delivering unparalleled customer experiences. With advanced toolsets and intelligent systems, businesses are closer to making more informed, strategic decisions. Elevate your logistical operations and customer satisfaction with the strategic integration of route scheduling solutions .

Now, it’s your turn. Reflect on your current logistics complexities. How can your business benefit from implementing these key concepts and algorithms? Consider where you could incorporate these practices to streamline and revolutionize your daily operations.

Remember, in the world of dynamic business operations, mastering the TSP is not just an option, but a strategic imperative. As you move forward into 2024, embrace the art of solving the TSP. Unravel the potential, decipher the complexities, and unlock new horizons for your business.

Ready for the challenge?

What is route optimization?

Top route optimization algorithms

What is multi-stop route planning and why is it important?

What is multi stop route planning and why is it important?

How to optimize routes with Google Maps

7 benefits of using route scheduling software

Benefits of using route scheduling software

Why delivery route optimization is crucial

What does a route planning software do?

Truck route planning vs common route planning

‟Great resource for my small business”

P’s Patties

‟Great service and support from Metrobi”

Anna’s Taqueria

‟The quality of customer service is great!”

‟With Metrobi, we’re now doing home deliveries in the Greater Boston area”

GrandTen Distilling

• Route Optimization
• travelling salesman problem

• dynamic route optimization

• vehicle routing problem

• free route planning software

• truck route

• route planning software

• How to Start a Farm
• start a farm

• Charcuterie Supplies and Equipment
• charcuterie supplies

• Charcuterie Sales & Marketing
• charcuterie sales

• Farm Operations
• farm management

• Farm Equipment
• farm equipment

• Charcuterie Business
• charcuterie business

• Types of Shipping Methods
• International shipping

• Click and collect shipping

• omnichannel logistics

• Last Mile Delivery Glossary
• green transportation

• payload capacity

Success Stories

Rebel Bread

Diamond Bakery

Quinlan-Wasserman

DELIVER WITH METROBI

Grow with confidence

• Atlanta courier service
• Austin courier service
• Boston courier service
• Chicago courier service
• Denver courier service
• Miami courier service
• New York City courier service
• Los Angeles courier service
• Philadelphia courier service
• San Francisco courier service
• Washington DC courier service
• See all locations
• Driver Network
• Software Only

• 55 Court St, Boston, MA 02108
• [email protected]
• Team Metrobi
• Privacy policy
• Terms of service
• Write for us NEW

Refer us to a company, you earn $250 and they earn $250. Learn more

• Delivery Management Software
• Shopify Delivery Planner App
• Metrobi Delivery API NEW
• Zapiet: Pickup Delivery NEW
• See all integrations
• Metrobi vs. Onfleet
• Metrobi vs. Roadie
• Metrobi vs. Roadie Support
• See all comparisons
• Bulk Order Delivery Service
• Express Urgent Delivery Service
• Fixed Route Delivery Service
• On Demand Delivery Service
• Overnight Delivery Service
• Same Day Delivery Service
• Scheduled Delivery Service
• Wholesale Delivery Service
• See all delivery services
• Artisan Food
• Food Producers
• See all industries

Want to access our large pool of drivers?

We started Metrobi to take operations off your plate. We provide drivers (rated 4.97/5), dedicated operation managers (70% cheaper), and routing software with a receiver notification system.

Reset password New user? Sign up

Existing user? Log in

Traveling Salesperson Problem

Already have an account? Log in here.

A salesperson needs to visit a set of cities to sell their goods. They know how many cities they need to go to and the distances between each city. In what order should the salesperson visit each city exactly once so that they minimize their travel time and so that they end their journey in their city of origin?

The traveling salesperson problem is an extremely old problem in computer science that is an extension of the Hamiltonian Circuit Problem . It has important implications in complexity theory and the P versus NP problem because it is an NP-Complete problem . This means that a solution to this problem cannot be found in polynomial time (it takes superpolynomial time to compute an answer). In other words, as the number of vertices increases linearly, the computation time to solve the problem increases exponentially.

The following image is a simple example of a network of cities connected by edges of a specific distance. The origin city is also marked.

Network of cities

Here is the solution for that network, it has a distance traveled of only 14. Any other path that the salesman can takes will result in a path length that is more than 14.

Relationship to Graphs

Special kinds of tsp, importance for p vs np, applications.

The traveling salesperson problem can be modeled as a graph . Specifically, it is typical a directed, weighted graph. Each city acts as a vertex and each path between cities is an edge. Instead of distances, each edge has a weight associated with it. In this model, the goal of the traveling salesperson problem can be defined as finding a path that visits every vertex, returns to the original vertex, and minimizes total weight.

To that end, many graph algorithms can be used on this model. Search algorithms like breadth-first search (BFS) , depth-first search (DFS) , and Dijkstra's shortest path algorithm can certainly be used, however, they do not take into consideration that fact that every vertex must be visited.

The Traveling Salesperson Problem (TSP), an NP-Complete problem, is notoriously complicated to solve. That is because the greedy approach is so computational intensive. The greedy approach to solving this problem would be to try every single possible path and see which one is the fastest. Try this conceptual question to see if you have a grasp for how hard it is to solve.

For a fully connected map with \(n\) cities, how many total paths are possible for the traveling salesperson? Show Answer There are (n-1)! total paths the salesperson can take. The computation needed to solve this problem in this way grows far too quickly to be a reasonable solution. If this map has only 5 cities, there are \(4!\), or 24, paths. However, if the size of this map is increased to 20 cities, there will be \(1.22 \cdot 10^{17}\) paths!

The greedy approach to TSP would go like this:

• Find all possible paths.
• Find the cost of every paths.
• Choose the path with the lowest cost.

Another version of a greedy approach might be: At every step in the algorithm, choose the best possible path. This version might go a little quicker, but it's not guaranteed to find the best answer, or an answer at all since it might hit a dead end.

For NP-Hard problems (a subset of NP-Complete problems) like TSP, exact solutions can only be implemented in a reasonable amount of time for small input sizes (maps with few cities). Otherwise, the best approach we can do is provide a heuristic to help the problem move forward in an optimal way. However, these approaches cannot be proven to be optimal because they always have some sort of downside.

Small input sizes

As described, in a previous section , the greedy approach to this problem has a complexity of \(O(n!)\). However, there are some approaches that decrease this computation time.

The Held-Karp Algorithm is one of the earliest applications of dynamic programming . Its complexity is much lower than the greedy approach at \(O(n^2 2^n)\). Basically what this algorithm says is that every sub path along an optimal path is itself an optimal path. So, computing an optimal path is the same as computing many smaller subpaths and adding them together.

Heuristics are a way of ranking possible next steps in an algorithm in the hopes of cutting down computation time for the entire algorithm. They are often a tradeoff of some attribute - such as completeness, accuracy, or precision - in favor of speed. Heuristics exist for the traveling salesperson problem as well.

The most simple heuristic for this problem is the greedy heuristic. This heuristic simply says, at each step of the network traversal, choose the best next step. In other words, always choose the closest city that you have not yet visited. This heuristic seems like a good one because it is simple and intuitive, and it is even used in practice sometimes, however there are heuristics that are proven to be more effective.

Christofides algorithm is another heuristic. It produces at most 1.5 times the optimal weight for TSP. This algorithm involves finding a minimum spanning tree for the network. Next, it creates matchings for the cities of an odd degree (meaning they have an odd number of edges coming out of them), calculates an eulerian path , and converts back to a TSP path.

Even though it is typically impossible to optimally solve TSP problems, there are cases of TSP problems that can be solved if certain conditions hold.

The metric-TSP is an instance of TSP that satisfies this condition: The distance from city A to city B is less than or equal to the distance from city A to city C plus the distance from city C to city B. Or,

\[distance_{AB} \leq distance_{AC} + distance_{CB}\]

This is a condition that holds in the real world, but it can't always be expected to hold for every TSP problem. But, with this inequality in place, the approximated path will be no more than twice the optimal path. Even better, we can bound the solution to a \(3/2\) approximation by using Christofide's Algorithm .

The euclidean-TSP has an even stricter constraint on the TSP input. It states that all cities' edges in the network must obey euclidean distances . Recent advances have shown that approximation algorithms using euclidean minimum spanning trees have reduced the runtime of euclidean-TSP, even though they are also NP-hard. In practice, though, simpler heuristics are still used.

The P versus NP problem is one of the leading questions in modern computer science. It asks whether or not every problem whose solution can be verified in polynomial time by a computer can also be solved in polynomial time by a computer. TSP, for example, cannot be solved in polynomial time (at least that's what is currently theorized). However, TSP can be solved in polynomial time when it is phrased like this: Given a graph and an integer, x, decide if there is a path of length x or less than x . It's easy to see that given a proposed answer to this question, it is simple to check if it is less than or equal to x.

The traveling salesperson problem, like other problems that are NP-Complete, are very important to this debate. That is because if a polynomial time solution can be found to this problems, then \(P = NP\). As it stands, most scientists believe that \(P \ne NP\).

The traveling salesperson problem has many applications. The obvious ones are in the transportation space. Planning delivery routes or flight patterns, for example, would benefit immensly from breakthroughs is this problem or in the P versus NP problem .

However, this same logic can be applied to many facets of planning as well. In robotics, for instance, planning the order in which to drill holes in a circuit board is a complex task due to the sheer number of holes that must be drawn.

The best and most important application of TSP, however, comes from the fact that it is an NP-Complete problem. That means that its practical applications amount to the applications of any problem that is NP-Complete. So, if there are significant breakthroughs for TSP, that means that those exact same breakthrough can be applied to any problem in the NP-Complete class.

Problem Loading...

Note Loading...

Set Loading...

Travelling Salesman Problem: Python, C++ Algorithm

What is the Travelling Salesman Problem (TSP)?

Travelling Salesman Problem (TSP) is a classic combinatorics problem of theoretical computer science. The problem asks to find the shortest path in a graph with the condition of visiting all the nodes only one time and returning to the origin city.

The problem statement gives a list of cities along with the distances between each city.

Objective: To start from the origin city, visit other cities only once, and return to the original city again. Our target is to find the shortest possible path to complete the round-trip route.

Example of TSP

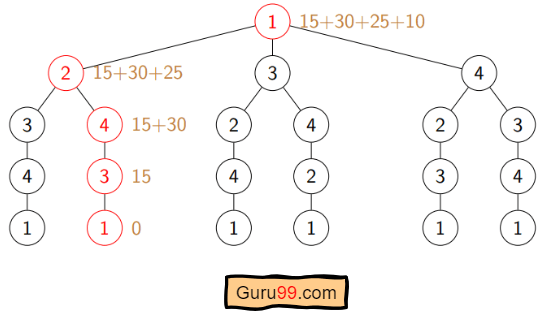
Here a graph is given where 1, 2, 3, and 4 represent the cities, and the weight associated with every edge represents the distance between those cities.

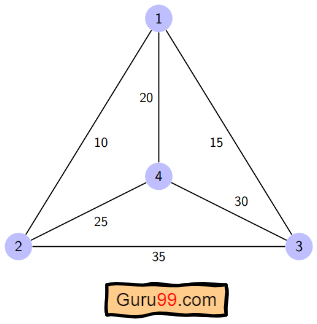
The goal is to find the shortest possible path for the tour that starts from the origin city, traverses the graph while only visiting the other cities or nodes once, and returns to the origin city.

For the above graph, the optimal route is to follow the minimum cost path: 1-2-4-3-1. And this shortest route would cost 10+25+30+15 =80

Different Solutions to Travelling Salesman Problem

Travelling Salesman Problem (TSP) is classified as a NP-hard problem due to having no polynomial time algorithm. The complexity increases exponentially by increasing the number of cities.

There are multiple ways to solve the traveling salesman problem (tsp). Some popular solutions are:

The brute force approach is the naive method for solving traveling salesman problems. In this approach, we first calculate all possible paths and then compare them. The number of paths in a graph consisting of n cities is n! It is computationally very expensive to solve the traveling salesman problem in this brute force approach.

The branch-and-bound method: The problem is broken down into sub-problems in this approach. The solution of those individual sub-problems would provide an optimal solution.

This tutorial will demonstrate a dynamic programming approach, the recursive version of this branch-and-bound method, to solve the traveling salesman problem.

Dynamic programming is such a method for seeking optimal solutions by analyzing all possible routes. It is one of the exact solution methods that solve traveling salesman problems through relatively higher cost than the greedy methods that provide a near-optimal solution.

The computational complexity of this approach is O(N^2 * 2^N) which is discussed later in this article.

The nearest neighbor method is a heuristic-based greedy approach where we choose the nearest neighbor node. This approach is computationally less expensive than the dynamic approach. But it does not provide the guarantee of an optimal solution. This method is used for near-optimal solutions.

Algorithm for Traveling Salesman Problem

We will use the dynamic programming approach to solve the Travelling Salesman Problem (TSP).

Before starting the algorithm, let’s get acquainted with some terminologies:

• A graph G=(V, E), which is a set of vertices and edges.
• V is the set of vertices.
• E is the set of edges.
• Vertices are connected through edges.
• Dist(i,j) denotes the non-negative distance between two vertices, i and j.

Let’s assume S is the subset of cities and belongs to {1, 2, 3, …, n} where 1, 2, 3…n are the cities and i, j are two cities in that subset. Now cost(i, S, j) is defined in such a way as the length of the shortest path visiting node in S, which is exactly once having the starting and ending point as i and j respectively.

For example, cost (1, {2, 3, 4}, 1) denotes the length of the shortest path where:

• Starting city is 1
• Cities 2, 3, and 4 are visited only once
• The ending point is 1

The dynamic programming algorithm would be:

• Set cost(i, , i) = 0, which means we start and end at i, and the cost is 0.
• When |S| > 1, we define cost(i, S, 1) = ∝ where i !=1 . Because initially, we do not know the exact cost to reach city i to city 1 through other cities.
• Now, we need to start at 1 and complete the tour. We need to select the next city in such a way-

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j) where i∈S and i≠j

For the given figure, the adjacency matrix would be the following:

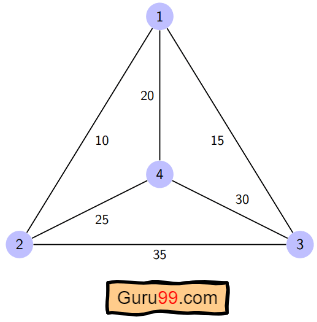
Let’s see how our algorithm works:

Step 1) We are considering our journey starting at city 1, visit other cities once and return to city 1.

Step 2) S is the subset of cities. According to our algorithm, for all |S| > 1, we will set the distance cost(i, S, 1) = ∝. Here cost(i, S, j) means we are starting at city i, visiting the cities of S once, and now we are at city j. We set this path cost as infinity because we do not know the distance yet. So the values will be the following:

Cost (2, {3, 4}, 1) = ∝ ; the notation denotes we are starting at city 2, going through cities 3, 4, and reaching 1. And the path cost is infinity. Similarly-

cost(3, {2, 4}, 1) = ∝

cost(4, {2, 3}, 1) = ∝

Step 3) Now, for all subsets of S, we need to find the following:

cost(i, S, j)=min cost (i, S−{i}, j)+dist(i,j), where j∈S and i≠j

That means the minimum cost path for starting at i, going through the subset of cities once, and returning to city j. Considering that the journey starts at city 1, the optimal path cost would be= cost(1, {other cities}, 1).

• Linear Search: Python, C++ Example
• DAA Tutorial PDF: Design and Analysis of Algorithms
• Heap Sort Algorithm (With Code in Python and C++)

Let’s find out how we could achieve that:

Now S = {1, 2, 3, 4}. There are four elements. Hence the number of subsets will be 2^4 or 16. Those subsets are-

1) |S| = Null:

2) |S| = 1:

{{1}, {2}, {3}, {4}}

3) |S| = 2:

{{1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}}

4) |S| = 3:

{{1, 2, 3}, {1, 2, 4}, {2, 3, 4}, {1, 3, 4}}

5) |S| = 4:

{{1, 2, 3, 4}}

As we are starting at 1, we could discard the subsets containing city 1.

The algorithm calculation:

1) |S| = Φ:

cost (2, Φ, 1) = dist(2, 1) = 10

cost (3, Φ, 1) = dist(3, 1) = 15

cost (4, Φ, 1) = dist(4, 1) = 20

cost (2, {3}, 1) = dist(2, 3) + cost (3, Φ, 1) = 35+15 = 50

cost (2, {4}, 1) = dist(2, 4) + cost (4, Φ, 1) = 25+20 = 45

cost (3, {2}, 1) = dist(3, 2) + cost (2, Φ, 1) = 35+10 = 45

cost (3, {4}, 1) = dist(3, 4) + cost (4, Φ, 1) = 30+20 = 50

cost (4, {2}, 1) = dist(4, 2) + cost (2, Φ, 1) = 25+10 = 35

cost (4, {3}, 1) = dist(4, 3) + cost (3, Φ, 1) = 30+15 = 45

cost (2, {3, 4}, 1) = min [ dist[2,3]+Cost(3,{4},1) = 35+50 = 85,

dist[2,4]+Cost(4,{3},1) = 25+45 = 70 ] = 70

cost (3, {2, 4}, 1) = min [ dist[3,2]+Cost(2,{4},1) = 35+45 = 80,

dist[3,4]+Cost(4,{2},1) = 30+35 = 65 ] = 65

cost (4, {2, 3}, 1) = min [ dist[4,2]+Cost(2,{3},1) = 25+50 = 75

dist[4,3]+Cost(3,{2},1) = 30+45 = 75 ] = 75

cost (1, {2, 3, 4}, 1) = min [ dist[1,2]+Cost(2,{3,4},1) = 10+70 = 80

dist[1,3]+Cost(3,{2,4},1) = 15+65 = 80

dist[1,4]+Cost(4,{2,3},1) = 20+75 = 95 ] = 80

So the optimal solution would be 1-2-4-3-1

Pseudo-code

Implementation in c/c++.

Here’s the implementation in C++ :

Implementation in Python

Academic solutions to tsp.

Computer scientists have spent years searching for an improved polynomial time algorithm for the Travelling Salesman Problem. Until now, the problem is still NP-hard.

Though some of the following solutions were published in recent years that have reduced the complexity to a certain degree:

• The classical symmetric TSP is solved by the Zero Suffix Method.
• The Biogeography‐based Optimization Algorithm is based on the migration strategy to solve the optimization problems that can be planned as TSP.
• Multi-Objective Evolutionary Algorithm is designed for solving multiple TSP based on NSGA-II.
• The Multi-Agent System solves the TSP of N cities with fixed resources.

Application of Traveling Salesman Problem

Travelling Salesman Problem (TSP) is applied in the real world in both its purest and modified forms. Some of those are:

• Planning, logistics, and manufacturing microchips : Chip insertion problems naturally arise in the microchip industry. Those problems can be planned as traveling salesman problems.
• DNA sequencing : Slight modification of the traveling salesman problem can be used in DNA sequencing. Here, the cities represent the DNA fragments, and the distance represents the similarity measure between two DNA fragments.
• Astronomy : The Travelling Salesman Problem is applied by astronomers to minimize the time spent observing various sources.
• Optimal control problem : Travelling Salesman Problem formulation can be applied in optimal control problems. There might be several other constraints added.

Complexity Analysis of TSP

So the total time complexity for an optimal solution would be the Number of nodes * Number of subproblems * time to solve each sub-problem. The time complexity can be defined as O(N 2 * 2^N).

• Space Complexity: The dynamic programming approach uses memory to store C(S, i), where S is a subset of the vertices set. There is a total of 2 N subsets for each node. So, the space complexity is O(2^N).

Next, you’ll learn about Sieve of Eratosthenes Algorithm

Help Center Help Center

• Help Center
• Trial Software
• Product Updates
• Documentation

Traveling Salesman Problem: Solver-Based

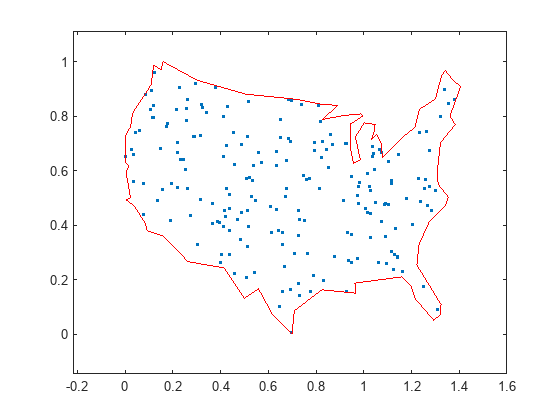
This example shows how to use binary integer programming to solve the classic traveling salesman problem. This problem involves finding the shortest closed tour (path) through a set of stops (cities). In this case there are 200 stops, but you can easily change the nStops variable to get a different problem size. You'll solve the initial problem and see that the solution has subtours. This means the optimal solution found doesn't give one continuous path through all the points, but instead has several disconnected loops. You'll then use an iterative process of determining the subtours, adding constraints, and rerunning the optimization until the subtours are eliminated.

For the problem-based approach, see Traveling Salesman Problem: Problem-Based .

Problem Formulation

Formulate the traveling salesman problem for integer linear programming as follows:

Generate all possible trips, meaning all distinct pairs of stops.

Calculate the distance for each trip.

The cost function to minimize is the sum of the trip distances for each trip in the tour.

The decision variables are binary, and associated with each trip, where each 1 represents a trip that exists on the tour, and each 0 represents a trip that is not on the tour.

To ensure that the tour includes every stop, include the linear constraint that each stop is on exactly two trips. This means one arrival and one departure from the stop.

Generate Stops

Generate random stops inside a crude polygonal representation of the continental U.S.

Calculate Distances Between Points

Because there are 200 stops, there are 19,900 trips, meaning 19,900 binary variables (# variables = 200 choose 2).

Generate all the trips, meaning all pairs of stops.

Calculate all the trip distances, assuming that the earth is flat in order to use the Pythagorean rule.

With this definition of the dist vector, the length of a tour is

dist'*x_tsp

where x_tsp is the binary solution vector. This is the distance of a tour that you try to minimize.

Create Graph and Draw Map

Represent the problem as a graph. Create a graph where the stops are nodes and the trips are edges.

Display the stops using a graph plot. Plot the nodes without the graph edges.

Constraints

Create the linear constraints that each stop has two associated trips, because there must be a trip to each stop and a trip departing each stop. This formulation works when the problem has at least three stops.

Binary Bounds

All decision variables are binary. Now, set the intcon argument to the number of decision variables, put a lower bound of 0 on each, and an upper bound of 1.

Optimize Using intlinprog

The problem is ready for solution. To suppress iterative output, turn off the default display.

Create a new graph with the solution trips as edges. To do so, round the solution in case some values are not exactly integers, and convert the resulting values to logical .

Visualize Solution

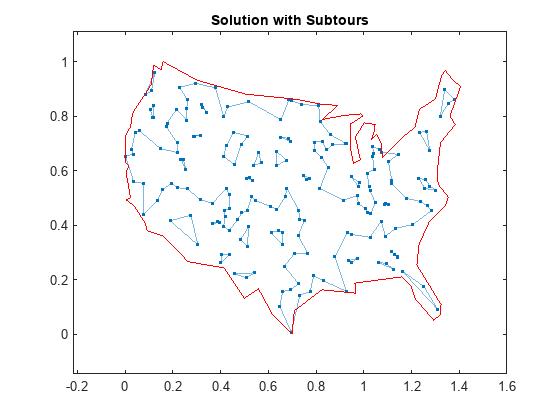
As can be seen on the map, the solution has several subtours. The constraints specified so far do not prevent these subtours from happening. In order to prevent any possible subtour from happening, you would need an incredibly large number of inequality constraints.

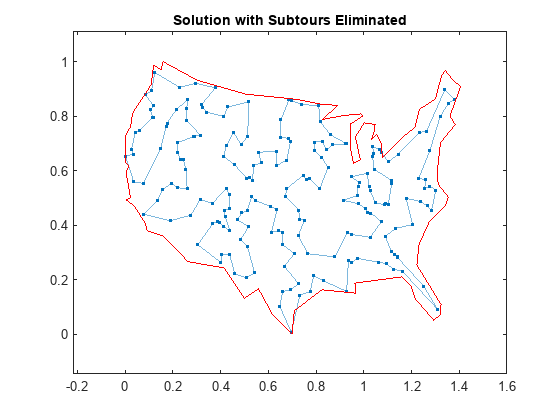
Subtour Constraints

Because you can't add all of the subtour constraints, take an iterative approach. Detect the subtours in the current solution, then add inequality constraints to prevent those particular subtours from happening. By doing this, you find a suitable tour in a few iterations.

Eliminate subtours with inequality constraints. An example of how this works is if you have five points in a subtour, then you have five lines connecting those points to create the subtour. Eliminate this subtour by implementing an inequality constraint to say there must be less than or equal to four lines between these five points.

Even more, find all lines between these five points, and constrain the solution not to have more than four of these lines present. This is a correct constraint because if five or more of the lines existed in a solution, then the solution would have a subtour (a graph with n nodes and n edges always contains a cycle).

Detect the subtours by identifying the connected components in Gsol , the graph built with the edges in the current solution. conncomp returns a vector with the number of the subtour to which each edge belongs.

Include the linear inequality constraints to eliminate subtours, and repeatedly call the solver, until just one subtour remains.

Solution Quality

The solution represents a feasible tour, because it is a single closed loop. But is it a minimal-cost tour? One way to find out is to examine the output structure.

The smallness of the absolute gap implies that the solution is either optimal or has a total length that is close to optimal.

Related Topics

• Traveling Salesman Problem: Problem-Based

MATLAB Command

You clicked a link that corresponds to this MATLAB command:

Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site

Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .

• Switzerland (English)
• Switzerland (Deutsch)
• Switzerland (Français)
• 中国 (English)

You can also select a web site from the following list:

How to Get Best Site Performance

Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.

• América Latina (Español)
• Canada (English)
• United States (English)
• Belgium (English)
• Denmark (English)
• Deutschland (Deutsch)
• España (Español)
• Finland (English)
• France (Français)
• Ireland (English)
• Italia (Italiano)
• Luxembourg (English)
• Netherlands (English)
• Norway (English)
• Österreich (Deutsch)
• Portugal (English)
• Sweden (English)
• United Kingdom (English)

Asia Pacific

• Australia (English)
• India (English)
• New Zealand (English)

Contact your local office

• Travelling salesman problem

The travelling salesman problem (often abbreviated to TSP) is a classic problem in graph theory . It has many applications, in many fields. It also has quite a few different solutions.

The problem

The problem is usually stated in terms of a salesman who needs to visit several towns before eventually returning to the starting point. There are various routes he could take, visiting the different towns in different orders. Here is an example:

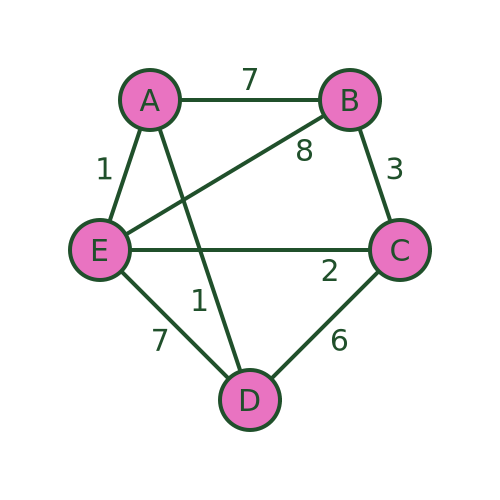
There are several different routes that will visit every town. For example, we could visit the towns in the order A , B , C , D , E , then back to A . Or we could use the route A , D , C , E , B then back to A .

But not all routes are possible. For example, we cannot use a route A , D , E , B , C and then back to A , because there is no road from C to A .

The aim is to find the route that visits all the towns with the minimum cost . The cost is shown as the weight of each edge in the graph. This might be the distance between the towns, or it might be some other measure. For example, it might be the time taken to travel between the towns, which might not be proportionate to the distance because some roads have lower speed limits or are more congested. Or, if the salesman was travelling by train, it might be the price of the tickets.

The salesman can decide to optimise for whatever measure he considers to be most important.

Alternative applications and variants

TSP applies to any problem that involves visiting various places in sequence. One example is a warehouse, where various items need to be fetched from different parts of a warehouse to collect the items for an order. In the simplest case, where one person fetches all the items for a single order and then packs and dispatches the items, a TSP algorithm can be used. Of course, a different route would be required for each order, which would be generated by the ordering system.

Another interesting example is printed circuit board (PCB) drilling. A PCB is the circuit board you will find inside any computer or other electronic device. They often need holes drilled in them, including mounting holes where the board is attached to the case and holes where component wires need to pass through the board. These holes are usually drilled by a robot drill that moves across the board to drill each hole in the correct place. TSP can be used to calculate the optimum drilling order.

The TSP algorithm can be applied to directed graphs (where the distance from A to B might be different to the distance from B to A ). Directed graphs can represent things like one-way streets (where the distance might not be the same in both directions) or flight costs (where the price of a single airline ticket might not be the same in both directions).

There are some variants of the TSP scenario. The mTSP problem covers the situation where there are several salesmen and exactly one salesman must visit each city. This applies to delivery vans, where there might be several delivery vans. The problem is to decide which parcels to place on each van and also to decide the route of each van.

The travelling purchaser problem is another variant. In that case, a purchaser needs to buy several items that are being sold in different places, potentially at different prices. The task is to purchase all the items, minimising the total cost (the cost of the items and the cost of travel). A simple approach would be to buy each item from the place where it is cheapest, in which case this becomes a simple TSP. However, it is not always worth buying every item from the cheapest place because sometimes the travel cost might outweigh the price difference.

In this article, we will only look at the basic TSP case.

Brute force algorithm

We will look at 3 potential algorithms here. There are many others. The first, and simplest, is the brute force approach.

We will assume that we start at vertex A . Since we intend to make a tour of the vertices (ie visit every vertex once and return to the original vertex) it doesn't matter which vertex we start at, the shortest loop will still be the same.

So we will start at A , visit nodes B , C , D , and E in some particular order, then return to A .

To find the shortest route, we will try every possible ordering of vertices B , C , D , E , and record the cost of each one. Then we can find the shortest.

For example, the ordering ABCDEA has a total cost of 7+3+6+7+1 = 24.

The ordering ABCEDA (i.e. swapping D and E ) has a total cost of 7+3+2+7+1 = 20.

Some routes, such as ADEBCA are impossible because a required road doesn't exist. We can just ignore those routes.

After evaluating every possible route, we are certain to find the shortest route (or routes, as several different routes may happen to have the same length that also happens to be the shortest length). In this case, the shortest route is AECBDA with a total length of 1+8+3+6+1 = 19.

The main problem with this algorithm is that it is very inefficient. In this example, since we have already decided that A is the start/end point, we must work out the visiting order for the 4 towns BCDE . We have 4 choices of the first town, 3 choices for the second town, 2 choices for the third town, and 1 choice for the fourth town. So there are 4! (factorial) combinations. That is only 24 combinations, which is no problem, you could even do it by hand.

If we had 10 towns (in addition to the home town) there would be 10! combinations, which is 3628800. Far too many to do by hand, but a modern PC might be able to do that in a fraction of a second if the algorithm was implemented efficiently.

If we had 20 towns, then the number of combinations would be of order 10 to the power 18. If we assume a computer that could evaluate a billion routes per second (which a typical PC would struggle to do, at least at the time of writing), that would take a billion seconds, which is several decades.

Of course, there are more powerful computers available, and maybe quantum computing will come into play soon, but that is only 20 towns. If we had 100 towns, the number of combinations would be around 10 to the power 157, and 1000 towns 10 to the power 2568. For some applications, it would be quite normal to have hundreds of vertices. The brute force method is impractical for all but the most trivial scenarios.

Nearest neighbour algorithm

The nearest neighbour algorithm is what we might call a naive attempt to find a good route with very little computation. The algorithm is quite simple and obvious, and it might seem like a good idea to someone who hasn't put very much thought into it. You start by visiting whichever town is closest to the starting point. Then each time you want to visit the next town, you look at the map and pick the closest town to wherever you happen to be (of course, you will ignore any towns that you have visited already). What could possibly go wrong?

Starting at A , we visit the nearest town that we haven't visited yet. In this case D and E are both distance 1 from A . We will (completely arbitrarily) always prioritise the connections in alphabetical order. So we pick D .

As an aside, if we had picked E instead we would get a different result. It might be better, but it is just as likely to be worse, so there is no reason to chose one over the other.

From D , the closest town is C with a distance of 6 (we can't pick A because we have already been there).

From C the closest town is E with distance 2. From E we have to go to B because we have already visited every other town - that is a distance of 8. And from B we must return to A with a distance of 7.

The final path is ADCEBA and the total distance is 1+6+2+8+7 = 24.

The path isn't the best, but it isn't terrible. This algorithm will often find a reasonable path, particularly if there is a natural shortest path. However, it can sometimes go badly wrong.

The basic problem is that the algorithm doesn't take account of the big picture. It just blindly stumbles from one town to whichever next town is closest.

In particular, the algorithm implicitly decides that the final step will be B to A . It does this based on the other distances, but without taking the distance BA into account. But what if, for example, there is a big lake between B and A that you have to drive all the way around? This might make the driving distance BA very large. A more sensible algorithm would avoid that road at all costs, but the nearest neighbour algorithm just blindly leads us there.

We can see this with this revised graph where BA has a distance of 50:

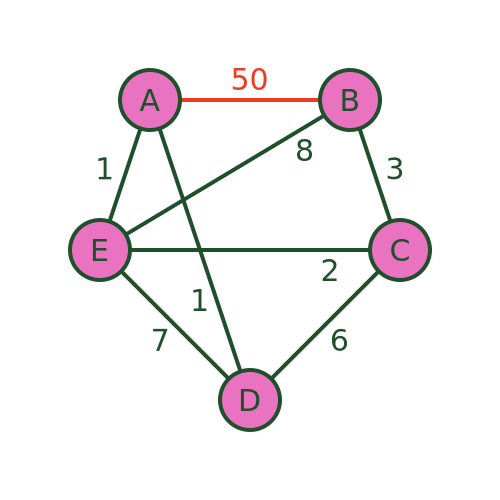
The algorithm will still recommend the same path because it never takes the distance BA into account. The path is still ADCEBA but the total distance is now 1+6+2+8+50 = 67. There are much better routes that avoid BA .

An even worse problem can occur if there is no road at all from B to A . The algorithm would still guide us to town B as the final visit. But in that case, it is impossible to get from B to A to complete the journey:

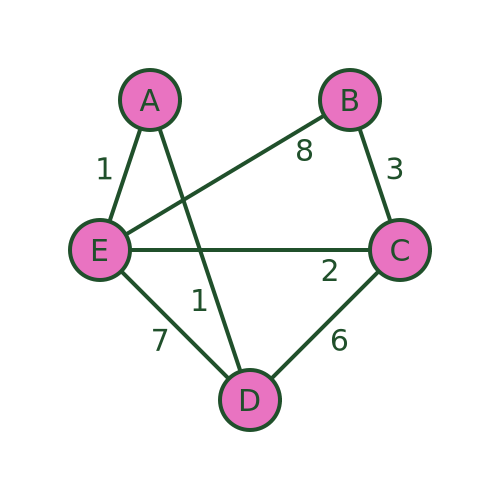
Bellman–Held–Karp algorithm

The Bellman–Held–Karp algorithm is a dynamic programming algorithm for solving TSP more efficiently than brute force. It is sometimes called the Held–Karp algorithm because it was discovered by Michael Held and Richard Karp, but it was also discovered independently by Richard Bellman at about the same time.

The algorithm assumes a complete graph (ie a graph where every vertex is connected to every other). However, it can be used with an incomplete graph like the one we have been using. To do this, we simply add extra the missing connections (shown below in grey) and assign them a very large distance (for example 1000). This ensures that the missing connections will never form part of the shortest path:

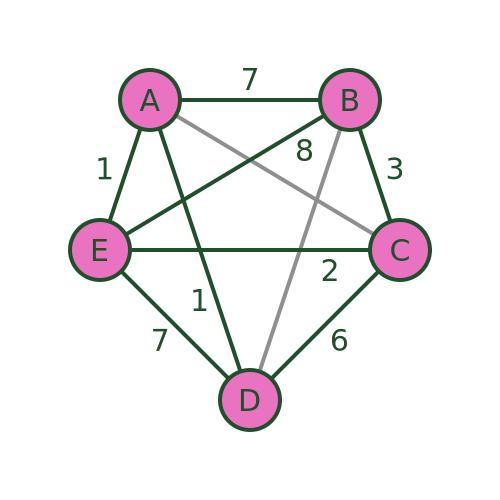
The technique works by incrementally calculating the shortest path for every possible set of 3 towns (starting from A ), then for every possible set of 4 towns, and so on until it eventually calculates the shortest path that goes from A via every other town and back to A .

Because the algorithm stores its intermediate calculations and discards non-optimal paths as early as possible, it is much more efficient than brute force.

We will use the following notation. We will use this to indicate the distance between towns A and B :

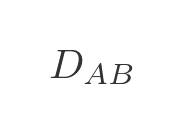
And we will use this to indicate the cost (ie the total distance) from A to C via B :

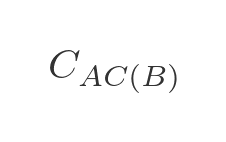
Here are some examples:

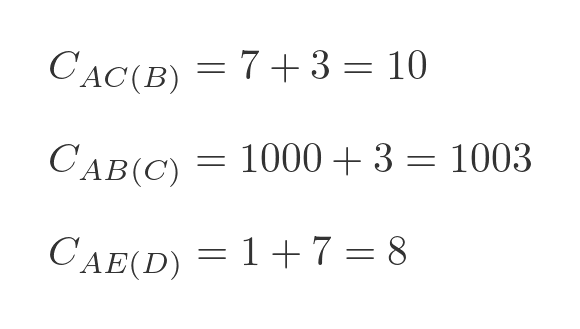
The first example is calculated by adding the distance AB to BC , which gives 10. The second example is calculated by adding AC to CB . But since there is no road from A to C , we give that a large dummy distance of 1000, so that total cost is 1003, which means it is never going to form a part of the shortest route. The third example is calculated by adding the distance AD to DE , which gives 8.

In the first step, we will calculate the value of every possible combination of 2 towns starting from A . There are 12 combinations: AB(C) , AB(D) , AB(E) , AC(B) , AC(D) , AC(E) , AD(B) , AD(C) , AD(E) , AE(B) , AE(C) , AE(D) .

These values will be stored for later use.

For step 2 we need to extend our notation slightly. We will use this to indicate the lowest cost from A to D via B and C (in either order):

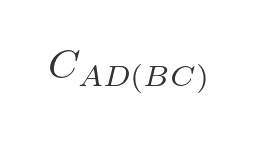
To be clear, this could represent one of two paths - ABCD or ACBD whichever is shorter. We can express this as a minimum of two values:

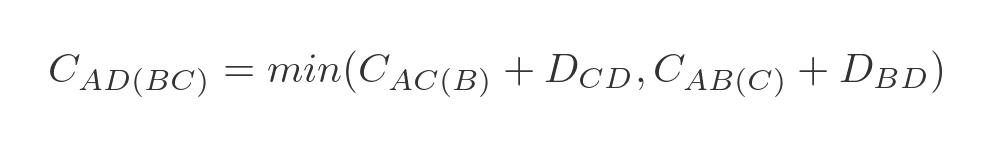
This represents the 2 ways to get from A to D via B and C :

• We can travel from A to C via B , and then from C to D .
• We can travel from A to B via C , and then from B to D .

We have already calculated A to C via B (and all the other combinations) in step 1, so all we need to do is add the values and find the smallest. In this case:

• A to C via B is 10, C to D is 6, so the total is 16.
• A to B via C is 1003, B to D is 1000, so the total is 2003.

Clearly, ABCD is the best route.

We need to repeat this for every possible combination of travelling from A to x via y and z . There are, again, 12 combinations: AB(CD) , AB(CE) , AB(DE) , AC(BD) , AC(BE) , AC(DE) , AD(BC) , AD(BE) , AD(CE) , AE(BC) , AE(BD) , AE(CD) .

We store these values, along with the optimal path, for later use.

In the next step, we calculate the optimal route for travelling from A to any other town via 3 intermediate towns. For example, travelling from A to E via B , C , and D (in the optimal order) is written as:

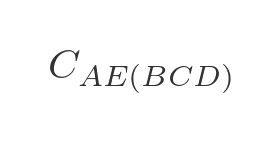
There are 3 paths to do this:

• A to D via B and C , then from D to E .
• A to C via B and D , then from C to E .
• A to B via C and D , then from B to E .

We will choose the shortest of these three paths:

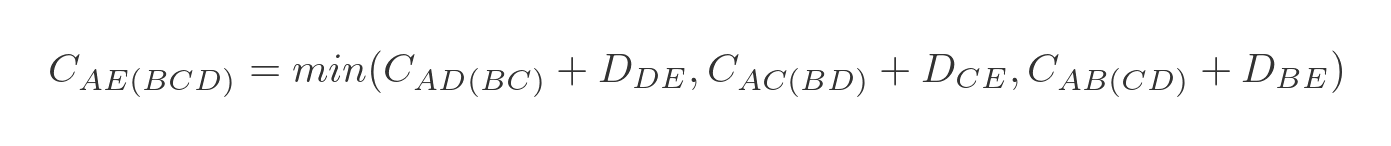
Again we have already calculated all the optimal intermediate paths. This time there are only 4 combinations we need to calculate: AB(CDE) , AC(BDE) , AD(BCE) , and AE(BCD) .

We are now in a position to calculate the optimal route for travelling from A back to A via all 4 other towns:

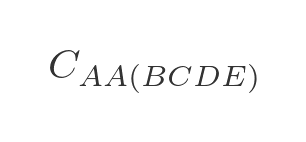
We need to evaluate each of the 4 options in step 3, adding on the extra distance to get back to A :

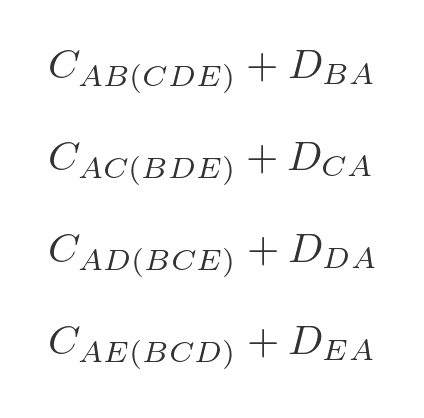
We can then choose the option that has the lowest total cost, and that will be the optimal route.

Performance

The performance of the Bellman–Held–Karp algorithm can be expressed in big-O notations as:

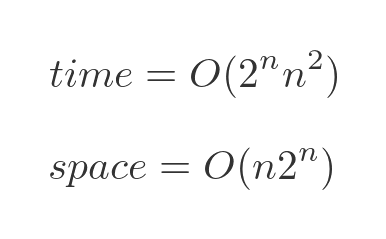
The time performance is approximately exponential. As the number of towns increases, the time taken will go up exponentially - each time an extra town is added, the time taken will double. We are ignoring the term in n squared because the exponential term is the most significant part.

Exponential growth is still quite bad, but it is far better than the factorial growth of the brute-force algorithm.

It is also important to notice that the algorithm requires memory to store the intermediate results, which also goes up approximately exponentially. The brute force algorithm doesn't have any significant memory requirements. However, that is usually an acceptable trade-off for a much better time performance.

The stages above describe how the algorithm works at a high level. We haven't gone into great detail about exactly how the algorithm keeps track of the various stages. Over the years since its discovery, a lot of work has been put into optimising the implementation. Optimising the implementation won't change the time complexity, which will still be roughly exponential. However, it might make the algorithm run several times faster than a poor implementation.

We won't cover this in detail, but if you ever need to use this algorithm for a serious purpose, it is worth considering using an existing, well-optimised implementation rather than trying to write it yourself. Unless you are just doing it for fun!

Other algorithms

Even the Bellman–Held–Karp algorithm has poor performance for modestly large numbers of towns. 100 towns, for example, would be well beyond the capabilities of a modern PC.

There are various heuristic algorithms that are capable of finding a good solution, but not necessarily the best possible solution, in a reasonable amount of time. I hope to cover these in a future article.

• Adjacency matrices
• The seven bridges of Königsberg
• Permutation matrices and graphs
• Dijkstra's algorithm

Join the GraphicMaths Newletter

Sign up using this form to receive an email when new content is added:

Popular tags

adder adjacency matrix alu and gate angle area argand diagram binary maths cartesian equation chain rule chord circle cofactor combinations complex modulus complex polygon complex power complex root cosh cosine cosine rule cpu cube decagon demorgans law derivative determinant diagonal directrix dodecagon eigenvalue eigenvector ellipse equilateral triangle euler eulers formula exponent exponential exterior angle first principles flip-flop focus gabriels horn gradient graph hendecagon heptagon hexagon horizontal hyperbola hyperbolic function hyperbolic functions infinity integration by parts integration by substitution interior angle inverse hyperbolic function inverse matrix irrational irregular polygon isosceles trapezium isosceles triangle kite koch curve l system line integral locus maclaurin series major axis matrix matrix algebra mean minor axis nand gate newton raphson method nonagon nor gate normal normal distribution not gate octagon or gate parabola parallelogram parametric equation pentagon perimeter permutations polar coordinates polynomial power probability probability distribution product rule proof pythagoras proof quadrilateral radians radius rectangle regular polygon rhombus root sech set set-reset flip-flop sine sine rule sinh sloping lines solving equations solving triangles square standard curves standard deviation star polygon statistics straight line graphs surface of revolution symmetry tangent tanh transformation transformations trapezium triangle turtle graphics variance vertical volume of revolution xnor gate xor gate

• Graph theory
• 7 bridges of Königsberg
• Binary numbers

Traveling Salesman Problem

The traveling salesman problem (TSP) asks the question, "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?".

This project

• The goal of this site is to be an educational resource to help visualize, learn, and develop different algorithms for the traveling salesman problem in a way that's easily accessible
• As you apply different algorithms, the current best path is saved and used as input to whatever you run next. (e.g. shortest path first -> branch and bound). The order in which you apply different algorithms to the problem is sometimes referred to the meta-heuristic strategy.

Heuristic algorithms

Heuristic algorithms attempt to find a good approximation of the optimal path within a more reasonable amount of time.

Construction - Build a path (e.g. shortest path)

• Shortest Path

Arbitrary Insertion

Furthest insertion.

• Nearest Insertion
• Convex Hull Insertion*
• Simulated Annealing*

Improvement - Attempt to take an existing constructed path and improve on it

• 2-Opt Inversion
• 2-Opt Reciprcal Exchange*

Exhaustive algorithms

Exhaustive algorithms will always find the best possible solution by evaluating every possible path. These algorithms are typically significantly more expensive then the heuristic algorithms discussed next. The exhaustive algorithms implemented so far include:

• Random Paths

Depth First Search (Brute Force)

• Branch and Bound (Cost)
• Branch and Bound (Cost, Intersections)*

Dependencies

These are the main tools used to build this site:

• web workers
• material-ui

Contributing

Pull requests are always welcome! Also, feel free to raise any ideas, suggestions, or bugs as an issue.

This is an exhaustive, brute-force algorithm. It is guaranteed to find the best possible path, however depending on the number of points in the traveling salesman problem it is likely impractical. For example,

• With 10 points there are 181,400 paths to evaluate.
• With 11 points, there are 1,814,000.
• With 12 points there are 19,960,000.
• With 20 points there are 60,820,000,000,000,000, give or take.
• With 25 points there are 310,200,000,000,000,000,000,000, give or take.

This is factorial growth, and it quickly makes the TSP impractical to brute force. That is why heuristics exist to give a good approximation of the best path, but it is very difficult to determine without a doubt what the best path is for a reasonably sized traveling salesman problem.

This is a recursive, depth-first-search algorithm, as follows:

• From the starting point
• For all other points not visited
• If there are no points left return the current cost/path
• Else, go to every remaining point and
• Mark that point as visited
• " recurse " through those paths (go back to 1. )

Implementation

Nearest neighbor.

This is a heuristic, greedy algorithm also known as nearest neighbor. It continually chooses the best looking option from the current state.

• sort the remaining available points based on cost (distance)
• Choose the closest point and go there
• Chosen point is no longer an "available point"
• Continue this way until there are no available points, and then return to the start.

Two-Opt inversion

This algorithm is also known as 2-opt, 2-opt mutation, and cross-aversion. The general goal is to find places where the path crosses over itself, and then "undo" that crossing. It repeats until there are no crossings. A characteristic of this algorithm is that afterwards the path is guaranteed to have no crossings.

• While a better path has not been found.
• For each pair of points:
• Reverse the path between the selected points.
• If the new path is cheaper (shorter), keep it and continue searching. Remember that we found a better path.
• If not, revert the path and continue searching.

This is a heuristic construction algorithm. It select a random point, and then figures out where the best place to put it will be.

• First, go to the closest point
• Choose a random point to go to
• Find the cheapest place to add it in the path
• Continue from #3 until there are no available points, and then return to the start.

This is an impractical, albeit exhaustive algorithm. It is here only for demonstration purposes, but will not find a reasonable path for traveling salesman problems above 7 or 8 points.

I consider it exhaustive because if it runs for infinity, eventually it will encounter every possible path.

• From the starting path
• Randomly shuffle the path
• If it's better, keep it
• If not, ditch it and keep going

Two-Opt Reciprocal Exchange

This algorithm is similar to the 2-opt mutation or inversion algorithm, although generally will find a less optimal path. However, the computational cost of calculating new solutions is less intensive.

The big difference with 2-opt mutation is not reversing the path between the 2 points. This algorithm is not always going to find a path that doesn't cross itself.

It could be worthwhile to try this algorithm prior to 2-opt inversion because of the cheaper cost of calculation, but probably not.

• Swap the points in the path. That is, go to point B before point A, continue along the same path, and go to point A where point B was.

Branch and Bound on Cost

This is a recursive algorithm, similar to depth first search, that is guaranteed to find the optimal solution.

The candidate solution space is generated by systematically traversing possible paths, and discarding large subsets of fruitless candidates by comparing the current solution to an upper and lower bound. In this case, the upper bound is the best path found so far.

While evaluating paths, if at any point the current solution is already more expensive (longer) than the best complete path discovered, there is no point continuing.

For example, imagine:

• A -> B -> C -> D -> E -> A was already found with a cost of 100.
• We are evaluating A -> C -> E, which has a cost of 110. There is no point evaluating the remaining solutions.

Instead of continuing to evaluate all of the child solutions from here, we can go down a different path, eliminating candidates not worth evaluating:

• A -> C -> E -> D -> B -> A
• A -> C -> E -> B -> D -> A

Implementation is very similar to depth first search, with the exception that we cut paths that are already longer than the current best.

This is a heuristic construction algorithm. It selects the closest point to the path, and then figures out where the best place to put it will be.

• Choose the point that is nearest to the current path

Branch and Bound (Cost, Intersections)

This is the same as branch and bound on cost, with an additional heuristic added to further minimize the search space.

While traversing paths, if at any point the path intersects (crosses over) itself, than backtrack and try the next way. It's been proven that an optimal path will never contain crossings.

Implementation is almost identical to branch and bound on cost only, with the added heuristic below:

This is a heuristic construction algorithm. It selects the furthest point from the path, and then figures out where the best place to put it will be.

• Choose the point that is furthest from any of the points on the path

Convex Hull

This is a heuristic construction algorithm. It starts by building the convex hull , and adding interior points from there. This implmentation uses another heuristic for insertion based on the ratio of the cost of adding the new point to the overall length of the segment, however any insertion algorithm could be applied after building the hull.

There are a number of algorithms to determine the convex hull. This implementation uses the gift wrapping algorithm .

In essence, the steps are:

• Determine the leftmost point
• Continually add the most counterclockwise point until the convex hull is formed
• For each remaining point p, find the segment i => j in the hull that minimizes cost(i -> p) + cost(p -> j) - cost(i -> j)
• Of those, choose p that minimizes cost(i -> p -> j) / cost(i -> j)
• Add p to the path between i and j
• Repeat from #3 until there are no remaining points

Simulated Annealing

Simulated annealing (SA) is a probabilistic technique for approximating the global optimum of a given function. Specifically, it is a metaheuristic to approximate global optimization in a large search space for an optimization problem.

For problems where finding an approximate global optimum is more important than finding a precise local optimum in a fixed amount of time, simulated annealing may be preferable to exact algorithms

Visualize algorithms for the traveling salesman problem. Use the controls below to plot points, choose an algorithm, and control execution. (Hint: try a construction alogorithm followed by an improvement algorithm)

Home  >   Blog  >   Travelling Salesman Problem: Definition, Algorithms & Solutions

Travelling Salesman Problem: Definition, Algorithms & Solutions

Explore the Traveling Salesman Problem, its algorithms, real-world applications, and practical solutions for optimizing delivery routes in logistics.

Table Of Contents

The Traveling Salesman Problem (TSP) is all about figuring out the shortest route for a salesperson to visit several cities, starting from one place and possibly ending at another. It's a well-known problem in computer science and operations research, with real-world uses in logistics and delivery.

There are many possible routes, but the goal is to find the one that covers the least distance or costs the least. This is what mathematicians and computer scientists have been working on for decades.

This isn’t just a theory problem. Using route optimization algorithms to find better routes can help delivery businesses make more money. It also helps to lower their greenhouse gas emissions by traveling less.

In theoretical computer science, the Traveling Salesman Problem (TSP) gets a lot of attention because it’s simple to explain but tough to solve. It’s a type of problem called combinatorial optimization and is known as NP-hard. This means the number of possible routes grows very quickly as more cities are added. Since there isn’t an efficient algorithm to solve TSP quickly, computer scientists use approximation algorithms. These methods test many different routes and pick the shortest one that costs the least.

You can solve the main problem by trying every possible route and picking the best one, but this brute-force method gets tricky as you add more destinations. The number of possible routes grows quickly, quickly overwhelming even the fastest computers. For just 10 destinations, there are over 300,000 possible routes. When there are 15 destinations, the number of routes can skyrocket to over 87 billion.

For bigger real-world Traveling Salesman Problems, tools like Google Maps Route Planner or Excel just don’t cut it anymore. Businesses turn to approximate solutions using quick TSP algorithms that use smart shortcuts. Trying to find the exact best route with dynamic programming isn’t usually practical for large problems.

In this post:

Three Common Algorithms for the Traveling Salesman Problem

Academic solutions for the traveling salesman problem, real-world uses of the traveling salesman problem, practical solutions for tsp and vrp, faqs about the travelling salesman problem.

1. Brute-Force Method

The brute-force method, sometimes called the naive approach, tries every possible route to find the shortest one. To use this method, you list all possible routes, calculate the distance for each one, and then pick the shortest route as the best solution.

This method works only for small problems and is mostly used for teaching in theoretical computer science. For larger problems, it's not practical.

2. Branch and Bound Method

The branch and bound method starts with an initial route, usually from the start point to the first city. It then explores different ways to extend the route by adding one city at a time. For each new route, it checks the length and compares it to the best route found so far. If the current route is longer than the best one, the algorithm "prunes" or cuts off that route, since it won’t be the best solution.

This pruning helps make the algorithm more efficient by focusing only on the most promising routes. The process continues until all possible routes have been checked, and the shortest one is chosen as the best solution. Branch and bound is a smart way to handle tough problems like the traveling salesman problem.

3. Nearest Neighbor Method

The nearest neighbor algorithm starts from a random point. From there, it finds the closest city that hasn't been visited yet and adds it to the route. This process is repeated by moving to the next closest unvisited city until all cities are included in the route. Finally, the route loops back to the starting city to complete the tour.

Although the nearest neighbor method is simple and fast, it often doesn't find the best possible route. For large or complex problems, it might end up with a route much longer than the optimal one. Still, it’s a useful starting point for solving the traveling salesman problem and can quickly provide a good enough solution.

This approach can also be used as the first step to create a decent route, which can then be improved with more advanced algorithms to get an even better solution.

Researchers have been working for years to find the best solutions for the Traveling Salesman Problem. Here are some of the recent advancements:

• Machine Learning for Vehicle Routing . MIT researchers use machine learning to tackle large, complex problems by breaking them into smaller, more manageable ones.
• Zero Suffix Method . Developed by researchers in India, this technique addresses the classical symmetric Traveling Salesman Problem.
• Biogeography-Based Optimization Algorithm . Inspired by animal migration patterns, this method uses nature's strategies to find optimization solutions.
• Meta-Heuristic Multi-Restart Iterated Local Search (MRSILS) . This approach claims to be more effective than genetic algorithms when working with clusters.
• Multi-Objective Evolutionary Algorithm . Based on the NSGA-II framework, this method solves multiple Traveling Salesman Problems simultaneously.
• Multi-Agent System . This system handles the Traveling Salesman Problem for N cities with fixed resources.

Even though solving the Traveling Salesman Problem is complex, approximate solutions—often using artificial intelligence and machine learning—are valuable across many industries.

For instance, TSP solutions can enhance efficiency in last-mile delivery. Last-mile delivery is the final stage in the supply chain, where goods move from a warehouse or depot to the customer. This step is also the biggest cost factor in the supply chain. It typically costs about $10.10, while customers only pay around $8.08, with companies covering the difference to stay competitive. Reducing these costs can significantly boost business profitability.

Reducing costs in last-mile delivery is a lot like solving a Vehicle Routing Problem (VRP) . VRP is a broader version of the Travelling Salesman Problem and is a key topic in mathematical optimization. Instead of finding just one best route, VRP focuses on finding the most efficient set of routes. It might involve multiple depots, many delivery locations, and several vehicles. Like the Travelling Salesman Problem, finding the best solution for VRP is also a tough challenge.

Academic solutions for the Traveling Salesman Problem (TSP) and Vehicle Routing Problem (VRP) aim to find the perfect answer to these tough problems. However, these solutions often aren't practical for real-world issues, especially when dealing with last-mile logistics.

Academic solvers focus on perfection, which means they can take a long time—sometimes hours, days, or even years—to compute the best solutions. For a delivery business that needs to plan routes every day , waiting that long isn't feasible. They need quick results to get their drivers and goods moving as soon as possible. Many businesses turn to tools like Google Maps Route Planner for a faster option.

In contrast, real-life TSP and VRP solvers use route optimization algorithms that provide near-perfect solutions in much less time. This allows delivery businesses to plan routes efficiently and swiftly, keeping their operations running smoothly.

What is a Hamiltonian cycle, and why is it key to the Travelling Salesman Problem?

A Hamiltonian cycle is a route in a graph that visits every point (vertex) exactly once before returning to where it started. It's essential for solving the Travelling Salesman Problem (TSP) because TSP is about finding the shortest Hamiltonian cycle that minimizes the total travel distance or time.

How does linear programming help with the Travelling Salesman Problem?

Linear programming (LP) is a mathematical technique used to optimize a linear function while meeting certain constraints. For the TSP, LP is useful for creating and solving a simpler version of the problem to find bounds or approximate solutions. It often involves relaxing some constraints, like integer constraints, to make the problem easier to handle.

What is recursion, and how does it apply to the Travelling Salesman Problem?

Recursion is a method where a function solves a problem by breaking it down into smaller, similar problems and calling itself to handle these smaller problems. In the context of the TSP, recursion is used in approaches like "Divide and Conquer," which breaks the main problem into smaller parts, making it easier to solve. This helps reduce repetitive calculations and speeds up finding a solution.

Why is time complexity important for understanding the Travelling Salesman Problem?

Time complexity measures how the time required to solve a problem grows as the size of the problem increases. For the Travelling Salesman Problem, knowing the time complexity is important because it helps estimate how long different algorithms will take, especially since TSP is NP-hard. As the number of cities grows, finding a solution can become very slow and challenging.

Similar posts

How to start a tow truck business in 2024.

Start a tow truck business in 2024 with our guide. Learn costs, regulations, and strategies to maximize profitability in this booming industry.

ELD Short-Haul Exemptions: Is Your Team Eligible?

Optimize routes, boost productivity, and ensure compliance with eLogii's fleet management solution. Simplify operations and maximize efficiency today!

What Is the Multi-Depot Vehicle Routing Problem? [+How to Solve It]

Want to know how to solve the Multi-Depot Vehicle Routing Problem? Read this guide to get a complete breakdown of MDVRP and how to do it.

The leading Route Optimization resource

Be the first to know when new articles are released. eLogii has a market-leading blog and resources centre designed specifically to help business across countless distribution and field-services sub sectors worldwide to succeed with actionable content and tips.

• Interview Q

DAA Tutorial

Asymptotic analysis, analysis of sorting, divide and conquer, lower bound theory, sorting in linear time, binary search trees, red black tree, dynamic programming, greedy algorithm, backtracking, shortest path, all-pairs shortest paths, maximum flow, sorting networks, complexity theory, approximation algo, string matching.

Interview Questions

• Send your Feedback to [email protected]

Help Others, Please Share

Learn Latest Tutorials

Transact-SQL

Reinforcement Learning

R Programming

React Native

Python Design Patterns

Python Pillow

Python Turtle

Preparation

Verbal Ability

Company Questions

Trending Technologies

Artificial Intelligence

Cloud Computing

Data Science

Machine Learning

B.Tech / MCA

Data Structures

Operating System

Computer Network

Compiler Design

Computer Organization

Discrete Mathematics

Ethical Hacking

Computer Graphics

Software Engineering

Web Technology

Cyber Security

C Programming

Control System

Data Mining

Data Warehouse

Route Optimization

Traveling salesman problem (tsp) and how tech can solve it.

Mar 2, 2020

11 mins read

Updated: Mar 9, 2023

Salespersons are required to travel frequently as a part of their job, with the aim of maximizing their business opportunities. However, their daily schedules are often subject to sudden changes due to scheduled and last-minute customer appointments, making it difficult for them to plan optimal travel routes. As a result, salespersons are forced to take longer routes to reach their destinations, which can result in missed appointments and lost business opportunities.

What is the Traveling Salesman Problem (TSP)? 

The Traveling Salesman Problem (TSP) involves finding the shortest possible route to multiple destinations and returning to the starting point. However, this is a complex task due to various constraints such as traffic, last-minute customer requests, and strict delivery windows. Successfully solving the TSP challenge can optimize supply chains and reduce logistics costs, making it an important problem to tackle.

Despite its seemingly simple definition, the TSP becomes increasingly difficult as more cities are added to the itinerary. For example, when delivering to six cities, there could be up to 360 possible routes to consider. Finding the most efficient and feasible path requires evaluating every possible route, which is a computationally challenging task. This has been an ongoing problem since the 1990s.

The TSP has relevance in various industries, such as astronomy, computer science, car navigation, agri-business, airline crew scheduling, computer-generated art, internet planning, logistics planning and scheduling, and microchip production.

What is the objective of TSP?

The problem statement for the Traveling Salesman Problem (TSP) has remained the same over the years: “Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city and returns to the origin city?” This was one of the most well-formulated optimizations in 1930 and remains a powerful solution for logistics-related problems. Variations in TSP problems have since made a disruptive difference in many other areas, including DNA sequencing.

TSP is no longer just about the problem of a salesman traveling to multiple cities in the least amount of time, using the least amount of money, while traveling the shortest distance. It now involves the world gearing towards the Fourth Industrial Revolution.

As cutting-edge technology is being integrated into manufacturing, TSP provides access to a wide variety of operations. For instance, a TSP variation could help design an efficient microchip. Similarly, an asymmetric version of TSP can optimize the set-up cost of a paint manufacturing plant by rearranging the vicinity of colors.

Is the Traveling Salesman Problem solvable?

Considering the basic problem itself, optimizing the logistics of a traveling salesman is under more monetary pressure than ever in history. Even if the problem is kept within city limits, it would be significant enough to become news. This is a real problem at a time when convenience is preferred over everything. A country’s GDP depends on its e-commerce purchases, which is something TSP enthusiasts didn’t foresee five decades ago.

India’s e-commerce industry is expected to contribute $300 billion by 2030, and the entire burden of it rests on the backseat of a delivery bike or transport. There are significant costs associated with this, particularly with return logistics being a pain point. What complicates the TSP logic further is the ground reality where the whole market is dependent upon cash-on-delivery, making it impossible to determine if a delivery will earn its cost back at times.

The problem also manifests itself in ride-sharing. Those who carpool to work heavily depend on affordable and comfortable transportation, and the twice-a-day practice that occurs during rush hour is not easy on anyone. There is added time and pressure for picking up each passenger, constant deviation from the main route to drop off others, and stress associated with it cannot be optimized.

Why is the Traveling Salesman Problem crucial to solve?

The Traveling Salesman Problem is a serious challenge for the logistics and supply chain industry because it involves optimizing the delivery routes for multiple destinations while considering various constraints such as traffic, delivery windows, and customer requests.

With multiple vehicles, more cities and multiple sales professionals, TSP becomes more challenging to solve. Not solving the TSP makes it difficult for sales professionals to efficiently reach their customers, and lead to a fall in business revenues.

Solving traveling salesman problems benefit businesses in numerous ways:

• Saves fuel and reduces the hours traveled by the sales and field professionals 
• Minimizes the distance traveled, thereby reducing the carbon footprint considerably
• Timely meetings with clients and on-time delivery of goods 
• Elevate last-mile customer experience for delivery and field service businesses

Why is Traveling Salesman Problem challenging to solve? 

In theory, solving the Traveling Salesman Problem (TSP) is relatively simple as it involves finding the shortest route for every trip within a city. However, as the number of cities increases, manually solving TSP becomes increasingly difficult. With just 10 cities, the permutations and combinations are already numerous. Adding just five more cities can exponentially increase the number of possible solutions.

It’s impossible to find an algorithm that solves every single TSP problem. There are also some constraints that make TSP more challenging to solve:

• No automated records of scheduled and last-minute business appointments 
• Traffic congestion
• Sudden change of routes 
• Increasing number of last-minute business appointments 
• Stricter customer time windows 
• Rising operational fleet costs

All these constraints give a clear insight that TSP is a real-world problem. It is impossible to solve this challenge with even the best of your manual efforts. Thus, it is necessary to harness the power of technology to manage the TSP problem efficiently.

Using the Hungarian method to solve the Travelling Salesman Problem

To feel the intensity of the problem closely, one can try solving it using the Hungarian method. If one assumes that a delivery executive makes 15 stops in a day, it would still be too large to optimize by hand. In the ride-sharing example where the car has to make four stops—picking up three passengers and returning to the point of origin—costs need to be allocated between rides. It is important not to repeat the same route twice and to solve the TSP to arrive at the minimum cost.

The calculation may seem quite simple at the moment, but scaling the execution of such optimized routes to handle deliveries worth $300 billion is a huge challenge. It would not only overwhelm one’s mind but quite possibly the RAM of one’s computer too. It seems unfair that such a large computational problem, which has taken decades to solve, has suddenly become so large that only a few have the power to tackle it.

How does Artificial Intelligence technology help in solving the Traveling Salesman Problem? 

Modern enterprises want to attract customers by providing superior service. A customer that interacts with an enterprise for a business opportunity wants the business to value their needs. 

Most customers make business decisions based on how salespeople from an enterprise respond to their requirements. The crucial aspect that they look out for in a salesperson is whether they are able to be on time for business appointments. A salesperson that travels to multiple locations should ensure they attend business appointments on time.

The Traveling Salesman Problem makes it way more difficult for salespersons to make their business appointments on time and reach their sales targets. With a lot of complexities involved in routes traveled, it is necessary for them to employ the right technology to counter them. Artificial Intelligence (AI) plays an active role in helping businesses counter route inefficiencies and solve TSP.

AI combines human intuition with complex mathematics in real-time. It analyzes a massive amount of data clearly and quickly. It mainly helps a modern enterprise to make operational, strategic and tactical decisions.

Here’s how AI solved TSP in many modern enterprises. 

Makes optimized decisions for each vehicle and route

With increasing business appointments, it would be difficult for enterprise businesses to control operational fleet costs . It is highly challenging to manage crucial business appointments without the help of technology, especially when the business handles multiple vehicles and multiple salespersons.

AI technology helps operation managers in a business to prepare and assign optimal sales schedules for their workforce. By taking into account vicinity, vehicle capacity, customer time window, skills of sales professionals, driver skills and so on, it generates optimal appointment schedules. These optimal schedules help the businesses strictly adhere to the Service Line of Agreement (SLA)

Read:      The Definitive Guide to Logistics Route Optimization

Saves fuel and labor costs

According to the “An Analysis of the Operational Costs of Trucking: 2022 Update”, the average fuel cost per mile decreased further from $0.308 in 2020 to $0.296 in 2021.

Since the outbreak of the Covid-19 pandemic in 2020, fuel costs have been at record low levels. However, as the world moves towards a post-pandemic stage in 2023, fuel costs have started to rise steadily. The Ukraine-Russia war in 2022 and its trade shocks have had a significant impact on fuel prices, resulting in a sharp increase. As a result, fuel costs have become a larger proportion of operational costs for carriers in 2023.

The increasing number of appointments on a daily basis for salespersons makes it difficult for businesses to minimize fuel costs.

Employing the right technology like AI will help salespersons complete the maximum number of customer appointments by traveling a minimal distance. Its optimally allocated route plans reduce the traveling time and help businesses avoid wastage of fuel and labor costs.

Recognize the right addresses

When you are in a rush to complete your sales visits, unclear addresses can induce delays. If the driver is going to ride in an unfamiliar area, delays will increase. These delays can even cause missed appointments.

By using an AI application like route optimization software , enterprise businesses can avoid delays caused due to incorrect addresses. Its competent geocoding capabilities convert unclear or incomplete text addresses into geographical coordinates , thereby reducing the chances of reaching wrong customer locations.

Reduces cost per mile

According to the “An Analysis of the Operational Costs of Trucking: 2022 Update” by the American Transport Research Institute, the average cost per mile of trucks continued to decrease from $1.646 in 2020 to $1.585 in 2021.

As fuel costs continue to rise and the world moves towards a post-pandemic period, there is a potential for an increase in the average cost per mile for trucks. This poses a challenge for modern enterprise businesses who want their salespersons to reach their targets without increasing operational fleet costs. To achieve their sales targets, salespersons need to attend more business appointments.

AI technology with its algorithms factors business goals and delivery constraints to come up with efficient routes. Its optimal route recommendations enable salespersons to take the cost-minimizing route, thereby attending a maximum number of business appointments in a day and minimizing cost per mile. 

Improves productivity 

What happens when salespersons attend business appointments in locations where they may not have many opportunities? It results in deadhead or empty miles. Empty miles kill the productivity of the fleet, and drive up operational costs considerably. 

AI technology coupled with data insights helps modern enterprise businesses analyze their past performance of sales appointments. It helps them identify business opportunities that incur huge costs and work out new ways to counter them. Based on historical data, it assists stakeholders of a business to rightsize their fleet requirements and direct them to locations where higher demand is expected. The past data records and predictive capabilities of AI help them implement strategies that improve productivity of their sales professionals.

With modern enterprise businesses struggling from incorrect routes and delays, it has become highly-crucial to solve TSP situations. Scientists have been working on solving the TSP problem for decades. But the modern AI-backed routing software has gone closer towards solving traveling salesman problems with their complex algorithms and enhanced route planning capabilities.

The Locus Dispatch Management Platform is the best-in-class tool that has helped many enterprise businesses solve their traveling salesman problems. Its algorithms help sales professionals generate the most efficient schedules for any complicated routes without any manual interference. By employing its AI capabilities, you can increase the number of appointments with your customers by traveling a minimal distance, thereby making sales visits more optimal.

To build the most efficient routes for your sales schedules and counter TSP effectively, try a demo with Locus now!

Related Tags:

Healthcare / Pharmaceutical

Route optimization for the pharmaceutical industry: countering last-mile delivery problems.

Feb 28, 2020

Pharmaceutical organizations spend on average 6% of their revenue on logistics- World Health Organization and Parenteral Drug Association statistics (WHO and PDA).  The pharmaceutical industry has been successful in creating life-saving drugs through advanced research and clinical trials. Transportation and storage determine the major success of pharma products globally. A small mistake in logistics can […]

CEP and 3PL

The future of e-commerce lies in achieving same-day and slot-based deliveries.

Mar 4, 2020

Convenience. That’s the word of our times.  With all the apps doing the rounds, everything happens in an instant. Have a thought that the world should know? Type it, tweet it. Have a photo that you took on your weekend cycling trip, upload and post it with a crazy caption on Instagram. Hungry? Food from […]

• Schedule a Demo

EDITOR’S PICKS

Transportation Management System

Traditional tmss are dead: the rise of the modern tms.

Mehul Kapadia

Apr 3, 2024

Retail & CPG

7 ways retailers can reduce delivery costs.

Mar 27, 2024

Navigating Returns: Five Strategies for Shippers to Reduce Return to Origin

Prateek Shetty

Nov 28, 2023

MOST POPULAR

The Rise of Hub and Spoke Distribution Model in Modern Supply Chains

Shweta Sarma

Apr 24, 2020

How to Calculate the Cost of Transport

Jun 9, 2023

SUBSCRIBE TO OUR NEWSLETTER

Stay up to date with the latest marketing, sales, and service tips and news

Discover more from Locus Blog

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

Traveling Salesman Problem

The traveling salesman problem is mentioned by the character Larry Fleinhardt in the Season 2 episode " Rampage " (2006) of the television crime drama NUMB3RS .

Explore with Wolfram|Alpha

More things to try:

• traveling salesman problem
• geometric mean 12, 17

Cite this as:

Weisstein, Eric W. "Traveling Salesman Problem." From MathWorld --A Wolfram Web Resource. https://mathworld.wolfram.com/TravelingSalesmanProblem.html

Subject classifications

Manage commercial vehicles with the new-age Fleet Management Software

Streamline your scattered workforce with Field Force Management Software

Optimize your delivery process with last mile delivery software

How to Enhance the Field Sales Team’s Performance? The Secret is Out!

What is PUDO? How Does PickUp and DropOff Location Work?

GPS Hardware Types of hardware devices we support for utmost security.

GPS Hardware Manufacturers Top GPS hardware manufacturers, our solutions are supportive of.

Blog Carefully Curated articles to update you on industrial trends.

White Paper Insightful papers and analysis on essential subject matters.

Glossary Offer clients a modern, all-in-one payroll and HR system you’ll both love

About Us Get to know TrackoBit: our team, ethos, values, and vision.

Careers Join the most dynamic cult of coders, creatives and changemakers.

Tech Support Learn about our technical support team and services in detail.

Events Check out the exhibitions where we left our marks and conquered.

Contact Us Connect with us and let us know how we can be of service.

What is a Travelling Salesman Problem (TSP)? Explained!

• Author: Diksha Bhandari
• Read Time: 9 min
• Published: September 14, 2023
• Last Update: July 4th, 2024

Table of Contents

• Route Planning
• Driver Behaviour
• Last Mile Delivery
• Asset Tracking
• Dispatch Management
• Fuel Management
• Route Optimisation
• Electric Vehicle
• Roster Management
• Vehicle Tracking
• TrackoMile Industries
• TrackoBit Industries
• Sensor Integration
• GPS Trackers and Hardware
• Tech and Beyond
• TrackoField
• What's New
• Employee Management
• Field Sales And Service
• Task and Workflow
• GPS Software
• Lead Management
• Fleet Management
• Leave And Attendance
• Video telematics
• TrackoField Industries

Want to know what a travelling salesman problem (TSP) is? Need solutions to real-life TSP challenges. Learn here. 

Do you also look for the shortest route on Google Maps before embarking on a trip?

I am sure, you know multiple routes to reach the office, the mall, or your desired location, but checking on the internet before leaving home has become a ritual. It becomes all the more important to refer to maps when you have to pick up friends or colleagues along the way.

‘ADD STOPS’

Yes, you are right! 💯

That’s what solving the TSP challenge using software means!

What is a Travelling Salesman Problem (TSP)?

The traveling salesman problem is the popular combinatorial optimisation challenge in mathematics and computer science. The prime objective of the problem is to determine the shortest possible route a salesperson must take to cover a set of locations in one go and then return to the starting point.

Addressing travelling salesman challenges and their optimisation are more relevant in this time and age, especially in the supply chain, logistics and delivery space.

TSP may result in delayed deliveries and slimming profits as it’s not easy for delivery agents to choose the most viable and cost-effective route in real-time.

What are Traveling Salesman Problem Challenges to Solve?

When a salesperson is in the field hopping from one client site to another, finding out the best and the shortest route is an added pressure on the agent. In today’s day and age, distance isn’t the only factor that defines efficiency. There are several factors, such as time, fuel consumption, capacity, etc. that together define efficiency.

However, addressing the travelling salesman challenges involves mitigating a few unavoidable challenges along the way that field agents face themselves.

1. Time Constraints

Sales agents often have a tight schedule with multiple deliveries to make with a short TAT. Similarly, in TSP, optimising routes to minimise travel time is a fundamental challenge.

2. Last-minute Changes

Eleventh-hour changes are not a new concept for salespeople. They encounter urgent visits and last-minute cancellations a lot. Similarly, TSP solutions must be adaptable to handle dynamic scenarios and route modifications.

3. Resource Efficiency

Just as salespersons aim at reducing fuel costs and ensuring on-time deliveries, TSP solutions such as TrackoMile must strive for resource optimisation by reducing travel distances and delivery TAT.

4. Objective Diversification

While solving the travelling salesman problem (TSP) , optimising multiple objectives such as cost, time, and environmental factors adds complexity as solutions need to balance conflicting goals.

5. Combinatorial Complexity

TSP is a combinatorial optimisation problem, which means it involves complicated mathematical calculations with numerous variables. Sometimes, complex scenarios get further intricate as multiple variables are involved.

6. Adaptability and Scalability

Similarly, how sales agents adjust to the routes on the fly, the route algorithm must be flexible and responsive to real-time changes such as spiking volumes, vehicle breakdown or traffic slow down. A TSP solution must have a good appetite to handle large datasets and complex networks.

Also Read 4 Key Solutions for Fuel Management System 2023

Top 5 Solutions to The Travelling Salesman Problem

The traveling salesman problem solutions offer various trade-offs between computational intricacies and the quality of the resolution, allowing practitioners to choose the best-suited approach based on their needs and problems.

Here are the Top 5 solutions to the Traveling Salesman Problem (TSP) :

1. Brute Force Algorithm

The Brute Force algorithm is a straight approach to solving the Traveling Salesman Problem (TSP). It systematically explores all possible routes to identify the shortest one among them all. While it guarantees an optimal solution, its downside lies in its major time complexity, making it practical only for small TSP challenges.

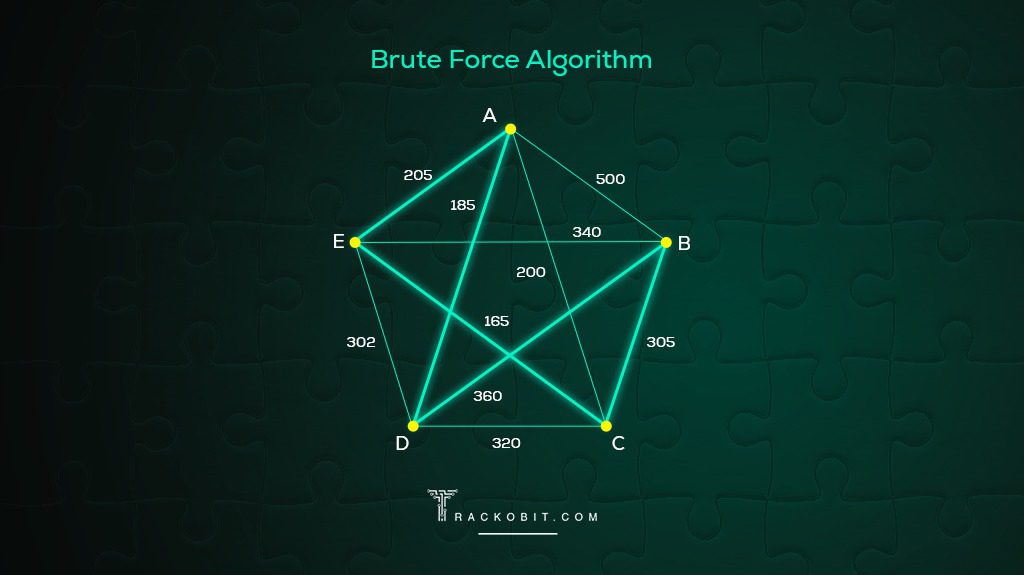
2. Nearest Neighbour Algorithm

The Nearest Neighbour method is the simplest heuristic for the TSP. It starts from the first location and repeatedly selects the closest unvisited location to form a tour. Although it is quick to implement this method, it may always yield the optimal solution for it prioritises proximity over other factors.

3. Genetic Algorithm

This technique or method draws inspiration from nature itself. They evolve TSP solutions through selection, crossovers and mutation. They pick the best routes and mix them up. This creates new routes that might be even better. Then, they keep the best ones and repeat the mixing and picking process. Survival of the fittest in the true sense.

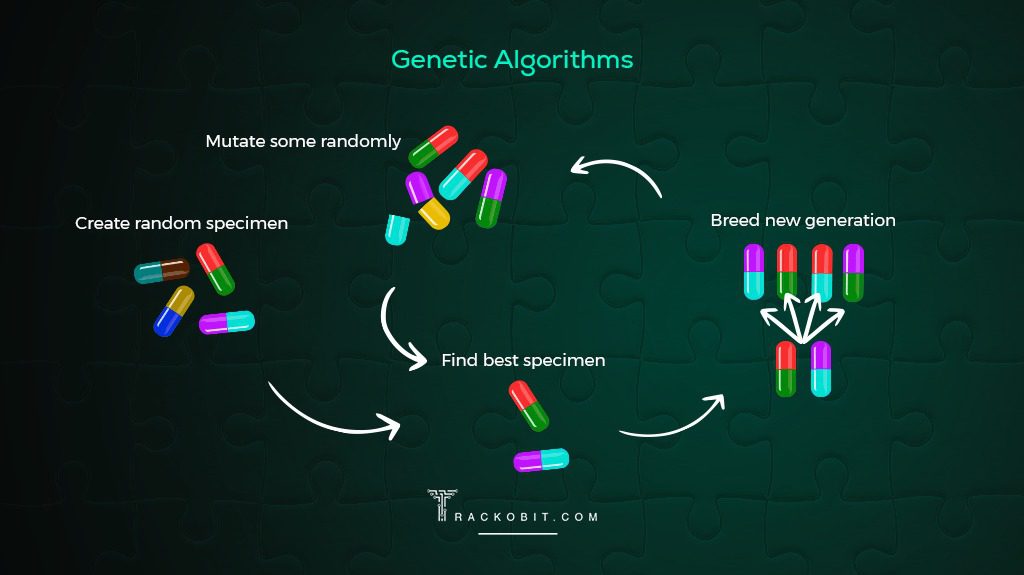
4. Ant Colony Optimisation (ACO)

Ants have a tendency to leave pheromones on the shorter routes they find, calling fellow ants on the same route. They keep leaving more pheromones on the shorter routes they find. Over time, the collective behaviour of the ants causes them to converge on the shortest route. Inspired by the nature of ants, ACO finds the shortest route by analysing the trails of data left by artificial ants based on the strength of these data trails.

5. Dynamic Programming

Dynamic Programming is like solving a puzzle, step-by-step, by breaking it into smaller pieces. In TSP challenges, it finds the best route to visit all locations. It begins with figuring out the shortest route between two locations; then it builds on that to find ways to more locations. It’s a smart TSP solution for small scenarios but may require significant memory resources for larger and more complex problems.

What Are Real-world Travelling Salesman Problem Applications?

The Traveling Salesman Problem (TSP) has a wide array of applications across various domains due to its relevance in optimising routes and sequences. Here are several crucial real-word TSP applications and implementations in the real world.

1. TSP implementation in Logistics and Delivery Services

The logistics and supply chain sectors have the widest TSP applications.

• Courier, Express & Parcel : Companies like FedEx, UPS, and DHL rely on TSP algorithms to optimise delivery routes for their fleet of delivery trucks. By finding the most efficient sequence of stops, they minimise fuel consumption , reduce delivery TAT, and save on operational overheads too.
• On-demand Delivery : Food delivery companies, instant grocery delivery apps and at-home appointment platforms like Swiggy, BlinkIt and UrbanCompany, respectively, leverage TSP solutions to ensure timely delivery. Enhancing the customer experience and increasing the number of deliveries each rider can make.

2. TSP Applications in Transportation and Urban Planning Waste collection routes, Traffic light synchronisation, optic cable installation, etc. are some areas where TSP Solutions works like a knight in shining armour. Other real-world TSP applications include

• Public Transport : City planners and public transport agencies use TSP principles to design bus, tram and train routes that reduce travel for passengers.
• Emergency Service Dispatch : Ambulance services, Police PCR vans employ TSP algorithms to dispatch vehicles quickly and efficiently in response to emergency calls. Finding the shortest route to reach the incident location can save lives.
• Urban Mobility Solution : In the era of ride-sharing and on-demand mobility apps like Uber, Ola, Lyft, etc., real-world TSP applications become prominent. TSP solutions optimise the route to destinations, ensuring quick and cost-effective transportation.

Other significant real-life applications of the Travelling Salesman Problem are

• TSP in Healthcare and Medical Research – for DNA sequencing and understanding genetic patterns and diseases.
• TSP in Manufacturing and Production – In circuit board manufacturing and job scheduling of technicians.
• TSP in Robotics and Autonomous Vehicles -Self-driving cars and drones use TSP-like algorithms for efficient navigation.

Solving the Travelling Salesman Problem – Last Mile Delivery Route Optimisation

Route optimisation is the key to efficient last-mile delivery . In order to attain flawless route optimisation, the software must solve the traveling salesman problem every step of the way.

Why it’s essential to solve TSP for Last Mile Delivery?

In simple and minimal words, solving TSP problems helps in many ways:

• Saves Time : It makes deliveries faster, so your customers get orders sooner.
• Customer Satisfaction : Fast deliveries give you an edge over the competition and enhance customer experience too.
• Saves Money : It reduces fuel wastage and vehicle wear, making deliveries cheaper.
• Environment Friendly : It lowers pollution by using fewer vehicles and shorter routes.
• Happy Staff: Drivers and dispatchers have less stress and can finish their work faster.

How do we solve the travelling salesman problem for last-mile delivery?

Solving TSP challenges for Last-mile delivery is like solving a big jigsaw puzzle. There are a hundred thousand addresses to visit daily. The software must find the shortest and most optimised route to them and come back to the starting point at the end.

• Our route optimisation software , TrackoMile, leverages capacity management , routing algorithms and robust rule engines to present the most optimal combination of delivery addresses. Thereby giving the most optimally planned routes or trips.
• All delivery managers have to do is upload the CSV file of the addresses or integrate TrackoMile to their CRM to fetch the delivery addresses. Now trip allocation, route optimisation, dispatch and everything else happen in a few clicks.
• ETA when the delivery is en route, POD when the order is delivered successfully, and trip analysis, are added features to simplify overall operations.

The Vehicle Routing Problem is very similar to TSP, with wide applications in logistics, delivery services and transportation. While TSP focuses on finding the shortest route for a single traveller visiting various locations, VRP deals with multiple vehicles serving multiple customers, considering added constraints like vehicle capacity, TATs and more.

How Can AI Help in Solving Traveling Salesman Problem (TSP)?

AI or Artificial Intelligence are becoming the driving force for business growth across various industrial sectors. AI particularly aids in solving the Traveling Salesman Problem(TSP) in the logistics and delivery sector by employing advanced algorithms and techniques. What are a few tricks up AI’s sleeves that help in automating TSP resolution? Let’s find out!

1. Advanced Algorithms

AI algorithms such as Genetic Algorithms, ACO, simulated annealing and a few others mentioned above, tackle complex Travelling Salesman Problem scenarios.

2. Machine Learning

Gathering information from historical data and optimising routes based on real-time insights is what AI is best for. Machine learning models are trained to adapt to changing conditions, like traffic, weather and delivery constraints, to provide a more accurate plan of action.

3. Parallel Computing

AIi enables the use of a parallel computing process, which means solving multiple segments of TSP simultaneously. This accelerates the problem-solving process for large-scale challenges.

4. Heuristic Improvement

TSP Heuristics powered by AI can groom initial solutions, gradually improving their results over time. These heuristics can be applied iteratively by AI to reach better results.

5. Hybrid Approaches

Applying hybrid algorithms is not a new technique to refine techniques and produce more accurate results. AI on top of it singles out data-oriented combinations that work the best in varied use cases.

Wrapping Up!

The travelling salesman problem’s importance lies in its real-world applications. Whether optimising delivery routes, planning manufacturing processes or organising circuit board drilling, finding the most efficient way to cover multiple locations is crucial to minimise costs and save time.

The TSP problems have evolved over the years, and so have TSP algorithms, heuristics and solutions. With the advent of advanced technologies such as GPS and machine learning, TSP continues to adapt and find new applications in emerging fields, cementing its status as a fundamental problem in optimization theory and a valuable tool for various industries. Mobility automation software like Trackobit, TrackoMile and TrackoField resort to TSP heuristics to solve challenges along the way.

Read Blog – Best Delivery Route Planner Apps for 2023

Traveling Salesman Problem FAQs

What is tsp.

TSP is an abbreviation for Traveling Salesman Problem. It’s the routing problem that deals with finding the shortest route to travel to a combination of locations in the most optimal manner.

Is Travelling Salesman Problem Solvable?

Yes, the Traveling Salesman Problem (TSP) is solvable, but the time to find the solution can grow proportionately with an increase in the number of locations. With the evolution of travelling salesman problem applications, various TSP algorithms and heuristics, their hybrids have also emerged.

Wh at is the objective of TSP?

The objective of the Traveling Salesman Problem (TSP) is to find the shortest possible route that covers all given locations or waypoints and comes back to the starting point with the least resource utilisation.

Diksha Bhandari

Currently creating SaaSy content strategies for TrackoBit and TrackoField, this content professional has dedicated a decade of her life to enriching her portfolio and continues to do so. In addition to playing with words and spilling SaaS, she has a passion for traveling to the mountains and sipping on adrak wali chai.

• Author Showcase
• All Blog Post

Never Miss a Beat

Thank you for reaching out! We'll speak to you soon.

In the meantime, why not find out more about us, explore our products, or visit our blog?

Stay Updated on tech, telematics and mobility. Don't miss out on the latest in the industry.

Cookie Consent

We use cookies to enhance and personalize your browsing experience. By continuing to use our website, you agree to our Privacy Policy.

• Data Structures & Algorithms
• DSA - Overview
• DSA - Environment Setup
• DSA - Algorithms Basics
• DSA - Asymptotic Analysis
• Data Structures
• DSA - Data Structure Basics
• DSA - Data Structures and Types
• DSA - Array Data Structure
• Linked Lists
• DSA - Linked List Data Structure
• DSA - Doubly Linked List Data Structure
• DSA - Circular Linked List Data Structure
• Stack & Queue
• DSA - Stack Data Structure
• DSA - Expression Parsing
• DSA - Queue Data Structure
• Searching Algorithms
• DSA - Searching Algorithms
• DSA - Linear Search Algorithm
• DSA - Binary Search Algorithm
• DSA - Interpolation Search
• DSA - Jump Search Algorithm
• DSA - Exponential Search
• DSA - Fibonacci Search
• DSA - Sublist Search
• DSA - Hash Table
• Sorting Algorithms
• DSA - Sorting Algorithms
• DSA - Bubble Sort Algorithm
• DSA - Insertion Sort Algorithm
• DSA - Selection Sort Algorithm
• DSA - Merge Sort Algorithm
• DSA - Shell Sort Algorithm
• DSA - Heap Sort
• DSA - Bucket Sort Algorithm
• DSA - Counting Sort Algorithm
• DSA - Radix Sort Algorithm
• DSA - Quick Sort Algorithm
• Graph Data Structure
• DSA - Graph Data Structure
• DSA - Depth First Traversal
• DSA - Breadth First Traversal
• DSA - Spanning Tree
• Tree Data Structure
• DSA - Tree Data Structure
• DSA - Tree Traversal
• DSA - Binary Search Tree
• DSA - AVL Tree
• DSA - Red Black Trees
• DSA - B Trees
• DSA - B+ Trees
• DSA - Splay Trees
• DSA - Tries
• DSA - Heap Data Structure
• DSA - Recursion Algorithms
• DSA - Tower of Hanoi Using Recursion
• DSA - Fibonacci Series Using Recursion
• Divide and Conquer
• DSA - Divide and Conquer
• DSA - Max-Min Problem
• DSA - Strassen's Matrix Multiplication
• DSA - Karatsuba Algorithm
• Greedy Algorithms
• DSA - Greedy Algorithms
• DSA - Travelling Salesman Problem (Greedy Approach)
• DSA - Prim's Minimal Spanning Tree
• DSA - Kruskal's Minimal Spanning Tree
• DSA - Dijkstra's Shortest Path Algorithm
• DSA - Map Colouring Algorithm
• DSA - Fractional Knapsack Problem
• DSA - Job Sequencing with Deadline
• DSA - Optimal Merge Pattern Algorithm
• Dynamic Programming
• DSA - Dynamic Programming
• DSA - Matrix Chain Multiplication
• DSA - Floyd Warshall Algorithm
• DSA - 0-1 Knapsack Problem
• DSA - Longest Common Subsequence Algorithm
• DSA - Travelling Salesman Problem (Dynamic Approach)
• Approximation Algorithms
• DSA - Approximation Algorithms
• DSA - Vertex Cover Algorithm
• DSA - Set Cover Problem
• DSA - Travelling Salesman Problem (Approximation Approach)
• Randomized Algorithms
• DSA - Randomized Algorithms
• DSA - Randomized Quick Sort Algorithm
• DSA - Karger’s Minimum Cut Algorithm
• DSA - Fisher-Yates Shuffle Algorithm
• DSA Useful Resources
• DSA - Questions and Answers
• DSA - Quick Guide
• DSA - Useful Resources
• DSA - Discussion
• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Travelling Salesman Problem (Dynamic Approach)

Travelling salesman dynamic programming algorithm, implementation.

Travelling salesman problem is the most notorious computational problem. We can use brute-force approach to evaluate every possible tour and select the best one. For n number of vertices in a graph, there are (n−1)! number of possibilities. Thus, maintaining a higher complexity.

However, instead of using brute-force, using the dynamic programming approach will obtain the solution in lesser time, though there is no polynomial time algorithm.

Let us consider a graph G = (V,E) , where V is a set of cities and E is a set of weighted edges. An edge e(u, v) represents that vertices u and v are connected. Distance between vertex u and v is d(u, v) , which should be non-negative.

Suppose we have started at city 1 and after visiting some cities now we are in city j . Hence, this is a partial tour. We certainly need to know j , since this will determine which cities are most convenient to visit next. We also need to know all the cities visited so far, so that we don't repeat any of them. Hence, this is an appropriate sub-problem.

For a subset of cities S $\epsilon$ {1,2,3,...,n} that includes 1 , and j $\epsilon$ S, let C(S, j) be the length of the shortest path visiting each node in S exactly once, starting at 1 and ending at j .

When |S|> 1 , we define 𝑪 C(S,1)= $\propto$ since the path cannot start and end at 1.

Now, let express C(S, j) in terms of smaller sub-problems. We need to start at 1 and end at j . We should select the next city in such a way that

$$C\left ( S,j \right )\, =\, min\, C\left ( S\, -\, \left\{j \right\},i \right )\, +\, d\left ( i,j \right )\: where\: i\: \epsilon \: S\: and\: i\neq j$$

There are at the most 2 n .n sub-problems and each one takes linear time to solve. Therefore, the total running time is O(2 n .n 2 ) .

In the following example, we will illustrate the steps to solve the travelling salesman problem.

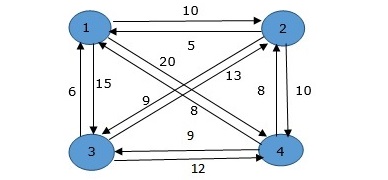
From the above graph, the following table is prepared.

$$Cost\left ( 2,\Phi ,1 \right )\, =\, d\left ( 2,1 \right )\,=\,5$$

$$Cost\left ( 3,\Phi ,1 \right )\, =\, d\left ( 3,1 \right )\, =\, 6$$

$$Cost\left ( 4,\Phi ,1 \right )\, =\, d\left ( 4,1 \right )\, =\, 8$$

$$Cost(i,s)=min\left\{Cos\left ( j,s-(j) \right )\, +\,d\left [ i,j \right ] \right\}$$

$$Cost(2,\left\{3 \right\},1)=d[2,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$

$$Cost(2,\left\{4 \right\},1)=d[2,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 10\, +\, 8\, =\, 18$$

$$Cost(3,\left\{2 \right\},1)=d[3,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 13\, +\, 5\, =\, 18$$

$$Cost(3,\left\{4 \right\},1)=d[3,4]\, +\, Cost\left ( 4,\Phi ,1 \right )\, =\, 12\, +\, 8\, =\, 20$$

$$Cost(4,\left\{3 \right\},1)=d[4,3]\, +\, Cost\left ( 3,\Phi ,1 \right )\, =\, 9\, +\, 6\, =\, 15$$

$$Cost(4,\left\{2 \right\},1)=d[4,2]\, +\, Cost\left ( 2,\Phi ,1 \right )\, =\, 8\, +\, 5\, =\, 13$$

$$Cost(2,\left\{3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 2,3 \right ]\,+ \,Cost\left ( 3,\left\{ 4\right\},1 \right )\, =\, 9\, +\, 20\, =\, 29 \\ d\left [ 2,4 \right ]\,+ \,Cost\left ( 4,\left\{ 3\right\},1 \right )\, =\, 10\, +\, 15\, =\, 25 \\ \end{matrix}\right.\, =\,25$$

$$Cost(3,\left\{2,4 \right\},1)=min\left\{\begin{matrix} d\left [ 3,2 \right ]\,+ \,Cost\left ( 2,\left\{ 4\right\},1 \right )\, =\, 13\, +\, 18\, =\, 31 \\ d\left [ 3,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2\right\},1 \right )\, =\, 12\, +\, 13\, =\, 25 \\ \end{matrix}\right.\, =\,25$$

$$Cost(4,\left\{2,3 \right\},1)=min\left\{\begin{matrix} d\left [ 4,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3\right\},1 \right )\, =\, 8\, +\, 15\, =\, 23 \\ d\left [ 4,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2\right\},1 \right )\, =\, 9\, +\, 18\, =\, 27 \\ \end{matrix}\right.\, =\,23$$

$$Cost(1,\left\{2,3,4 \right\},1)=min\left\{\begin{matrix} d\left [ 1,2 \right ]\,+ \,Cost\left ( 2,\left\{ 3,4\right\},1 \right )\, =\, 10\, +\, 25\, =\, 35 \\ d\left [ 1,3 \right ]\,+ \,Cost\left ( 3,\left\{ 2,4\right\},1 \right )\, =\, 15\, +\, 25\, =\, 40 \\ d\left [ 1,4 \right ]\,+ \,Cost\left ( 4,\left\{ 2,3\right\},1 \right )\, =\, 20\, +\, 23\, =\, 43 \\ \end{matrix}\right.\, =\, 35$$

The minimum cost path is 35.

Start from cost {1, {2, 3, 4}, 1}, we get the minimum value for d [1, 2]. When s = 3, select the path from 1 to 2 (cost is 10) then go backwards. When s = 2, we get the minimum value for d [4, 2]. Select the path from 2 to 4 (cost is 10) then go backwards.

When s = 1, we get the minimum value for d [4, 2] but 2 and 4 is already selected. Therefore, we select d [4, 3] (two possible values are 15 for d [2, 3] and d [4, 3], but our last node of the path is 4). Select path 4 to 3 (cost is 9), then go to s = ϕ step. We get the minimum value for d [3, 1] (cost is 6).

Following are the implementations of the above approach in various programming languages −

Travelling Salesman Problem | Greedy Approach

Given a 2D matrix tsp[][] , where each row has the array of distances from that indexed city to all the other cities and -1 denotes that there doesn’t exist a path between those two indexed cities. The task is to print minimum cost in TSP cycle. Examples:  

Input:   tsp[][] = {{-1, 10, 15, 20},  {10, -1, 35, 25},  {15, 35, -1, 30},  {20, 25, 30, -1}};  Below is the given graph:    Output: 80  Explanation:   We are trying to find out the path/route with the minimum cost such that our aim of visiting all cities once and return back to the source city is achieved. The path through which we can achieve that, can be represented as 1 -> 2 -> 4 -> 3 -> 1. Here, we started from city 1 and ended on the same visiting all other cities once on our way. The cost of our path/route is calculated as follows:  1 -> 2 = 10  2 -> 4 = 25  4 -> 3 = 30  3 -> 1 = 15  (All the costs are taken from the given 2D Array)  Hence, total cost = 10 + 25 + 30 + 15 = 80 Input:   tsp[][] = {{-1, 30, 25, 10},  {15, -1, 20, 40},  {10, 20, -1, 25},  {30, 10, 20, -1}};  Output: 50 

We introduced Travelling Salesman Problem and discussed Naive and Dynamic Programming Solutions for the problem in the previous post . Both of the solutions are infeasible. In fact, there is no polynomial-time solution available for this problem as the problem is a known NP-Hard problem. There are approximate algorithms to solve the problem though.  This problem can be related to the Hamiltonian Cycle problem , in a way that here we know a Hamiltonian cycle exists in the graph, but our job is to find the cycle with minimum cost. Also, in a particular TSP graph, there can be many hamiltonian cycles but we need to output only one that satisfies our required aim of the problem. Approach: This problem can be solved using Greedy Technique . Below are the steps: 

• A list that holds the indices of the cities in terms of the input matrix of distances between cities.
• Result array which will have all cities that can be displayed out to the console in any manner.
• Perform traversal on the given adjacency matrix tsp[][] for all the city and if the cost of the reaching any city from current city is less than current cost the update the cost.
• Generate the minimum path cycle using the above step and return there minimum cost.

Below is the implementation of the above approach:

Time Complexity: O(N 2 *log 2 N)  Auxiliary Space: O(N)  

Please Login to comment...

Similar reads.

• Competitive Programming
• Computer Subject
• Java Programs
• Algorithms-Greedy Algorithms
• How to Get a Free SSL Certificate
• Best SSL Certificates Provider in India
• Elon Musk's xAI releases Grok-2 AI assistant
• What is OpenAI SearchGPT? How it works and How to Get it?
• Content Improvement League 2024: From Good To A Great Article

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Algorithms for the Travelling Salesman Problem

Printables.com

• The Travelling Salesman Problem (TSP) is a classic algorithmic problem in the field of computer science and operations research, focusing on optimization. It seeks the shortest possible route that visits every point in a set of locations just once.
• The TSP problem is highly applicable in the logistics sector , particularly in route planning and optimization for delivery services. TSP solving algorithms help to reduce travel costs and time.
• Real-world applications often require adaptations because they involve additional constraints like time windows, vehicle capacity, and customer preferences.
• Advances in technology and algorithms have led to more practical solutions for real-world routing problems. These include heuristic and metaheuristic approaches that provide good solutions quickly.
• Tools like Routific use sophisticated algorithms and artificial intelligence to solve TSP and other complex routing problems, transforming theoretical solutions into practical business applications.

The Traveling Salesman Problem (TSP) is the challenge of finding the shortest path or shortest possible route for a salesperson to take, given a starting point, a number of cities (nodes), and optionally an ending point. It is a well-known algorithmic problem in the fields of computer science and operations research, with important real-world applications for logistics and delivery businesses.

There are obviously a lot of different routes to choose from, but finding the best one — the one that will require the least distance or cost — is what mathematicians and computer scientists have spent decades trying to solve.

It’s much more than just an academic problem in graph theory. Finding more efficient routes using route optimization algorithms increases profitability for delivery businesses, and reduces greenhouse gas emissions because it means less distance traveled.

In theoretical computer science, the TSP has commanded so much attention because it’s so easy to describe yet so difficult to solve. The TSP is known to be a combinatorial optimization problem that’s an NP-hard problem, which means that the number of possible solution sequences grows exponential with the number of cities. Computer scientists have not found any algorithm for solving travelling salesman problems in polynomial time, and therefore rely on approximation algorithms to try numerous permutations and select the shortest route with the minimum cost.

The main problem can be solved by calculating every permutation using a brute force approach, and selecting the optimal solution. However, as the number of destinations increases, the corresponding number of roundtrips grows exponentially, soon surpassing the capabilities of even the fastest computers. With 10 destinations, there can be more than 300,000 roundtrip permutations. With 15 destinations, the number of possible routes could exceed 87 billion.

For larger real-world travelling salesman problems, when manual methods such as Google Maps Route Planner or Excel route planner no longer suffice, businesses rely on approximate solutions that are sufficiently optimized by using fast tsp algorithms that rely on heuristics. Finding the exact optimal solution using dynamic programming is usually not practical for large problems.

Three popular Travelling Salesman Problem Algorithms

Here are some of the most popular solutions to the Travelling Salesman Problem:

1. The brute-force approach

TThe brute-force approach, also known as the naive approach, calculates and compares all possible permutations of routes or paths to determine the shortest unique solution. To solve the TSP using the brute-force approach, you must calculate the total number of routes and then draw and list all the possible routes. Calculate the distance of each route and then choose the shortest one — this is the optimal solution. 

This is only feasible for small problems, rarely useful beyond theoretical computer science tutorials.

2. The branch and bound method

The branch and bound algorithm starts by creating an initial route, typically from the starting point to the first node in a set of cities. Then, it systematically explores different permutations to extend the route beyond the first pair of cities, one node at a time. Each time a new node is added, the algorithm calculates the current path's length and compares it to the optimal route found so far. If the current path is already longer than the optimal route, it "bounds" or prunes that branch of the exploration, as it would not lead to a more optimal solution.

This pruning is the key to making the algorithm efficient. By discarding unpromising paths, the search space is narrowed down, and the algorithm can focus on exploring only the most promising paths. The process continues until all possible routes are explored, and the shortest one is identified as the optimal solution to the traveling salesman problem. Branch and bound is an effective greedy approach for tackling NP-hard optimization problems like the traveling salesman problem.

3. The nearest neighbor method

To implement the nearest neighbor algorithm, we begin at a randomly selected starting point. From there, we find the closest unvisited node and add it to the sequencing. Then, we move to the next node and repeat the process of finding the nearest unvisited node until all nodes are included in the tour. Finally, we return to the starting city to complete the cycle.

While the nearest neighbor approach is relatively easy to understand and quick to execute, it rarely finds the optimal solution for the traveling salesperson problem. It can be significantly longer than the optimal route, especially for large and complex instances. Nonetheless, the nearest neighbor algorithm serves as a good starting point for tackling the traveling salesman problem and can be useful when a quick and reasonably good solution is needed.

This greedy algorithm can be used effectively as a way to generate an initial feasible solution quickly, to then feed into a more sophisticated local search algorithm, which then tweaks the solution until a given stopping condition. ‍

How route optimization algorithms work to solve the Travelling Salesman Problem.

Academic tsp solutions.

Academics have spent years trying to find the best solution to the Travelling Salesman Problem The following solutions were published in recent years:

• Machine learning speeds up vehicle routing : MIT researchers apply Machine Learning methods to solve large np-complete problems by solving sub-problems.
• Zero Suffix Method : Developed by Indian researchers, this method solves the classical symmetric TSP. 
• Biogeography‐based Optimization Algorithm : This method is designed based on the animals’ migration strategy to solve the problem of optimization. 
• Meta-Heuristic Multi Restart Iterated Local Search (MRSILS): The proponents of this research asserted that the meta-heuristic MRSILS is more efficient than the Genetic Algorithms when clusters are used. 
• Multi-Objective Evolutionary Algorithm : This method is designed for solving multiple TSP based on NSGA-II. 
• Multi-Agent System : This system is designed to solve the TSP of N cities with fixed resource. 

Real-world TSP applications

Despite the complexity of solving the Travelling Salesman Problem, approximate solutions — often produced using artificial intelligence and machine learning — are useful in all verticals.

For example, TSP solutions can help the logistics sector improve efficiency in the last mile. Last mile delivery is the final link in a supply chain, when goods move from a transportation hub, like a depot or a warehouse, to the end customer. Last mile delivery is also the leading cost driver in the supply chain. It costs an average of $10.1, but the customer only pays an average of $8.08 because companies absorb some of the cost to stay competitive. So bringing that cost down has a direct effect on business profitability.

Minimizing costs in last mile delivery is essentially a Vehicle Routing Problem (VRP). VRP, a generalized version of the travelling salesman problem, is one of the most widely studied problems in mathematical optimization. Instead of one best path, it deals with finding the most efficient set of routes or paths. The problem may involve multiple depots, hundreds of delivery locations, and several vehicles. As with the travelling salesman problem, determining the best solution to VRP is NP-complete.

Real-life TSP and VRP solvers

While academic solutions to TSP and VRP aim to provide the optimal solution to these NP-hard problems, many of them aren’t practical when solving real world problems, especially when it comes to solving last mile logistical challenges.

That’s because academic solvers strive for perfection and thus take a long time to compute the optimal solutions – hours, days, and sometimes years. If a delivery business needs to plan daily routes, they need a route solution within a matter of minutes. Their business depends on delivery route planning software so they can get their drivers and their goods out the door as soon as possible. Another popular alternative is to use Google maps route planner .

Real-life TSP and VRP solvers use route optimization algorithms that find near-optimal solutions in a fraction of the time, giving delivery businesses the ability to plan routes quickly and efficiently.

If you want to know more about real-life TSP and VRP solvers, check out the resources below 👇

Route Optimization API - TSP Solver

Route Optimization API - VRP Solver

Frequently Asked Questions

What is a hamiltonian cycle, and why is it important in solving the travelling salesman problem.

A Hamiltonian cycle is a complete loop that visits every vertex in a graph exactly once before returning to the starting vertex. It's crucial for the TSP because the problem essentially seeks to find the shortest Hamiltonian cycle that minimizes travel distance or time.

What role does linear programming play in solving the Travelling Salesman Problem?

Linear programming (LP) is a mathematical method used to optimize a linear objective function, subject to linear equality and inequality constraints. In the context of TSP, LP can help in formulating and solving relaxation of the problem to find bounds or approximate solutions, often by ignoring the integer constraints (integer programming being a subset of LP) to simplify the problem.

What is recursion, and how does it apply to the Travelling Salesman Problem?

Recursion involves a function calling itself to solve smaller sub-problems of the same type as the larger problem. In TSP, recursion is used in methods like the "Divide and Conquer" strategy, breaking down the problem into smaller, manageable subsets, which can be particularly useful in dynamic programming solutions. It reduces redundancy and computation time, making the problem more manageable.

Why is understanding time complexity important when studying the Travelling Salesman Problem?

Time complexity refers to the computational complexity that describes the amount of computer time it takes to solve a problem. For TSP, understanding time complexity is crucial because it helps predict the performance of different algorithms, especially given that TSP is NP-hard and solutions can become impractically slow as the number of cities increases.

Related articles

Liked this article? See below for more recommended reading!

Solving the Vehicle Routing Problem (2024)

How To Optimize Multi-Stop Routes With Google Maps (2024)

How Route Optimization Impacts Our Earth

iMTSP: Solving Min-Max Multiple Traveling Salesman Problem with Imperative Learning

This paper considers a Min-Max Multiple Traveling Salesman Problem (MTSP), where the goal is to find a set of tours, one for each agent, to collectively visit all the cities while minimizing the length of the longest tour. Though MTSP has been widely studied, obtaining near-optimal solutions for large-scale problems is still challenging due to its NP-hardness. Recent efforts in data-driven methods face challenges of the need for hard-to-obtain supervision and issues with high variance in gradient estimations, leading to slow convergence and highly sub-optimal solutions. We address these issues by reformulating MTSP as a bilevel optimization problem, using the concept of imperative learning (IL). This involves introducing an allocation network that decomposes the MTSP into multiple single-agent traveling salesman problems (TSPs). The longest tour from these TSP solutions is then used to self-supervise the allocation network, resulting in a new self-supervised, bilevel, end-to-end learning framework, which we refer to as imperative MTSP (iMTSP). Additionally, to tackle the high-variance gradient issues during the optimization, we introduce a control variate-based gradient estimation algorithm. Our experiments showed that these innovative designs enable our gradient estimator to converge 20 × 20\times 20 × faster than the advanced reinforcement learning baseline, and find up to 80 % percent 80 80\% 80 % shorter tour length compared with Google OR-Tools MTSP solver, especially in large-scale problems (e.g. 1000 1000 1000 1000 cities and 15 15 15 15 agents).

I Introduction

The multiple traveling salesman problem (MTSP) seeks tours for multiple agents such that all cities are visited exactly once while minimizing an objective function defined over the tours. MTSP arises in numerous robotics topics that require a team of robots to collectively visit many target locations such as unmanned aerial vehicles path planning  [ 1 , 2 ] , automated agriculture  [ 3 ] , warehouse logistics  [ 4 ] . As their names suggest, Min-Sum MTSP minimizes the sum of tour lengths, while Min-Max MTSP minimizes the longest tour length, both of which are NP-hard  [ 5 ] to solve to optimality. 1 1 1 MTSP is challenging and renowned for its NP-hardness  [ 5 ] . Intuitively, MTSP involves many decision variables: both assigning the cities to the agents and determining the visiting order of the assigned cities. As an example, an MTSP with 100 100 100 100 cities and 10 10 10 10 agents involves 100 ! × 99 ! 10 ! × 89 ! ≈ 10 20000 100 99 10 89 superscript 10 20000 \frac{100!\times 99!}{10!\times 89!}\approx 10^{20000} divide start_ARG 100 ! × 99 ! end_ARG start_ARG 10 ! × 89 ! end_ARG ≈ 10 start_POSTSUPERSCRIPT 20000 end_POSTSUPERSCRIPT possible solutions, while the number of atoms in the observable universe is estimated to be “merely” in the range from 10 78 superscript 10 78 10^{78} 10 start_POSTSUPERSCRIPT 78 end_POSTSUPERSCRIPT to 10 82 superscript 10 82 10^{82} 10 start_POSTSUPERSCRIPT 82 end_POSTSUPERSCRIPT   [ 6 ] . In this paper, we focus on Min-Max MTSP while our method will also be applicable to Min-Sum MTSP. Min-Max MTSP is more often used when the application seeks to minimize the overall completion time  [ 7 ] . Due to the NP-hardness of MTSP, one must consider the trade-off between the solution optimality and the computational efficiency, since finding an optimal solution is often intractable for large problems.

A variety of classic (non-learning) approaches, including exact  [ 8 , 9 ] , approximation  [ 10 ] , and heuristic  [ 11 , 12 , 2 ] algorithms, have been developed to handle MTSP, but most of them consider minimizing the sum of tour lengths (Min-Sum), rather than the maximum tour length (Min-Max). In recent years, there has been a notable shift towards employing deep learning techniques to tackle TSP and MTSP  [ 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 , 21 , 22 ] . However, these methods still have fundamental limitations, particularly in their ability to generalize to unseen problem sizes, and in consistently finding high-quality solutions for large-scale problems. For deep learning-based methods that supervise the model with heuristic or exact solutions  [ 15 , 16 , 17 ] , they struggle with limited supervision on small-scale problems and lack feasible supervision for large-scale instances, leading to poor generalization. Reinforcement learning (RL)-based approaches  [ 14 , 18 , 19 , 20 ] usually exploit implementations of the policy gradient algorithm, such as the REINFORCE  [ 23 ] algorithm and its variants. These RL approaches face the issue of high-variance gradient estimations, which can result in slow convergence and highly sub-optimal solutions. Researchers have also developed strategies like training greedy policy networks  [ 19 , 18 , 21 ] or iteratively improving solutions  [ 22 ] , which often get stuck at local optima.

To enhance generalization and accelerate the training process, we reformulate the Min-Max MTSP as a bilevel optimization problem. This comprises an upper-level optimization that focuses on training a city allocation network, and a lower-level optimization that solves multiple signal-agent TSPs, inspired by imperative learning (IL)  [ 24 , 25 , 26 ] . Specifically, the allocation network is to assign each city to an agent, which decomposes the MTSP into multiple single-agent TSPs. Then, a classic TSP solver, which can quickly produce a near-optimal tour for a single-agent TSP with up to a few hundred cities, is employed to find a tour for each agent based on the allocation. A key aspect is that the upper-level optimization, namely the training of the allocation network, is supervised by the lower-level TSP solver. This metric-based supervision from the lower-level optimization results in an end-to-end, self-supervised framework for solving MTSP, which we refer to as imperative MTSP (iMTSP).

One technical obstacle when developing iMTSP is that the space of possible city allocations is discrete. As a result, the objective function, i.e., the maximum tour length given by the lower-level TSP solver, is non-differentiable to the city allocation, which prevents the back-propagation to the allocation network’s parameters. One of the solutions is to explore the policy gradient algorithm or the reparameterization trick  [ 27 ] , which often use Monte-Carlo methods to estimate the gradient. However, these methods can lead to gradient estimations with high variance since the space of city allocation is extremely large. To handle this difficulty, we introduce a control variate  [ 28 ] to reduce the variance of the gradient estimations. Parameterized by a trainable surrogate network running in parallel with the TSP solver, the control variate can be efficiently computed, and the overall algorithm can provide low variance gradient information through the non-differentiable solver and the discrete decision space. The main contributions of this paper are summarized as follows:

Framework : We formulate the MTSP as a bilevel optimization problem, introduce a new end-to-end, self-supervised framework for Min-Max MTSP. This decomposes a large-scale Min-Max MTSP into several smaller TSPs, each of which can be solved efficiently.

Methodology : To tackle the problem of bilevel optimization in discrete space, we introduce a control variate-based technique for back-propagation. This produces low-variance gradient estimations despite the non-differentiability of the lower-level optimization problem.

Experiments : We corroborate iMTSP in terms of efficiency and solution quality against both an RL-based and a classic (non-learning) methods. On large-scale problems, iMTSP achieves at most 80 % percent 80 80\% 80 % shorter tours and with only 1.6 % percent 1.6 1.6\% 1.6 % inference time compared with Google OR-Tools routing library  [ 29 ] . Also, iMTSP’s gradient estimator converges about 20 × 20\times 20 × faster and produces 3.2 ± 0.01 % plus-or-minus 3.2 percent 0.01 3.2\pm 0.01\% 3.2 ± 0.01 % shorter tours, compared with the RL-based approach  [ 14 ] .

II Related works

MTSP has been extensively studied. Analytical methods  [ 8 ] use graph theory, game theory, and combinatorial optimization, etc.  [ 30 ] , and can provide guarantees on solution optimality. However, these methods usually struggle at solving large-scale MTSP due to its NP-hardness.

Heuristic approaches for MTSP handle the challenge by decomposing the original problem into several phases which in turn reduces the computational burden of each phase. Examples are particle swarm optimization  [ 31 ] , ant colony optimization  [ 12 ] , etc  [ 32 , 33 ] . Although heuristic algorithms usually run faster than analytical approaches, they lack theoretic guarantees on solution quality and could produce highly sub-optimal solutions especially for large-scale problems with hundreds and thousands of cities.

Recently, researchers tried to solve MTSP with machine learning (ML) methods using recurrent neural networks (RNN)  [ 34 ] , transformer  [ 35 ] , etc. These learning-based methods usually scale well as the size of the problem increases. However, they may not generalize well to problem sizes outside the training set. As an early attempt  [ 17 ] , an RNN based method is developed and can handle TSP with up to 50 50 50 50 cities. Hu et al.  [ 14 ] propose a hybrid approach within the RL framework, which shows impressive generalization ability. However, their gradient estimator has high variance, which leads to slow convergence and sub-optimal solutions especially when dealing with large-scale problems. Other ML-based methods include  [ 19 , 18 , 21 , 22 ] . Note that most of them consider TSP instead of MTSP.

Imperative Learning As an emerging learning framework, imperative learning (IL) has inspired some pioneering works in simultaneous localization and mapping (SLAM)  [ 24 ] , path planning  [ 25 ] , and visual feature matching  [ 26 ] . The most significant difference between our work and theirs is that the lower-level optimization problems in their scenarios are all in continuous space, while iMTSP needs to deal with an extremely large discrete decision space.

Control Variate Control variate has been investigated by the ML community. In general, any policy gradient algorithm with a baseline or an actor-critic can be interpreted as an additive control variate method  [ 36 ] . Additionally, Grathwohl et.al.  [ 37 ] propose gradient estimators for a non-differentiable function with continuous and discrete inputs, respectively. Their insight is evaluating the control variate directly with a single sample estimation of the gradient variance. Our work leverages this insight. Gu et.al.  [ 38 ] produce a family of policy gradient methods using control variate to merge gradient information from both on-policy and off-policy updates. Control variate technique has also been used for meta-RL  [ 39 ] , federated learning  [ 40 ] , etc  [ 41 , 42 , 43 ] .

III Problem Formulation

where D ⁢ ( T j ) 𝐷 subscript 𝑇 𝑗 D(T_{j}) italic_D ( italic_T start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ) is the cost of route T j subscript 𝑇 𝑗 T_{j} italic_T start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT . For easier understanding, we use Euclidean distance as the cost in this paper, i.e.,:

This section first elaborates on the reformulation of MTSP as a bilevel optimization problem, and then introduces the forward computation of the our framework and the control variate-based optimization algorithm.

IV-A Reformulation of MTSP

The MTSP formulation in Section  III is reformulated as the following bilevel optimization problem: For each instance ( X , 𝐱 𝐝 , M ) 𝑋 subscript 𝐱 𝐝 𝑀 (X,\mathbf{x_{d}},M) ( italic_X , bold_x start_POSTSUBSCRIPT bold_d end_POSTSUBSCRIPT , italic_M ) , the upper-level problem is to assign each city to an agent, and the lower-level problem is to compute the visiting order of assigned cities for each agent. We define f 𝑓 f italic_f as the allocation network with parameters θ 𝜃 \mathbf{\theta} italic_θ , and g 𝑔 g italic_g as the single-agent TSP solver with parameters μ 𝜇 \mathbf{\mu} italic_μ . The imperative MTSP (iMTSP) is defined as:

where a j subscript 𝑎 𝑗 a_{j} italic_a start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT is the allocation for agent j 𝑗 j italic_j sampling from the probability matrix by row, and L 𝐿 L italic_L returns the maximum route length among all agents. s 𝑠 s italic_s is a surrogate network with parameter γ 𝛾 \gamma italic_γ , which will be explained in detail in Section  IV-C along with the specific definitions of upper-level objectives. Specifically, the upper-level optimization consists of two separate steps: the upper-level cost U θ subscript 𝑈 𝜃 U_{\theta} italic_U start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT is to optimize the allocation network f ⁢ ( θ ) 𝑓 𝜃 f(\theta) italic_f ( italic_θ ) , while U γ subscript 𝑈 𝛾 U_{\gamma} italic_U start_POSTSUBSCRIPT italic_γ end_POSTSUBSCRIPT is to optimize the surrogate network s ⁢ ( γ ) 𝑠 𝛾 s(\gamma) italic_s ( italic_γ ) . The framework of iMTSP is shown in Fig.  1 .

IV-B Forward Propagation Details

Iv-b 1 embedding, iv-b 2 allocation network.

As we have extracted the topological information into vector representations, we can now calculate the allocation matrix using the attention mechanism again. The keys 𝐤 ′ superscript 𝐤 ′ \mathbf{k}^{\prime} bold_k start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT and queries 𝐪 ′ superscript 𝐪 ′ \mathbf{q}^{\prime} bold_q start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT are computed from the city and agent embeddings, respectively, and the relative importance of each city to each agent is computed as:

The allocation matrix has a shape of N × M 𝑁 𝑀 N\times M italic_N × italic_M with N 𝑁 N italic_N and M 𝑀 M italic_M are the number of cities and agents, respectively. The model produces the final allocation by sampling each row of the allocation matrix. With the allocation, the MTSP is decomposed into M 𝑀 M italic_M TSPs. A classic TSP solver (such as Google OR-Tools) is invoked on each of the TSP to find the tour length of each TSP. The final return L 𝐿 L italic_L of the MTSP is the maximum tour length among all the TSPs. Because the TSP solver is non-differentiable and the allocation variables are discrete, network optimization is very challenging.

IV-C Optimization

Now we demonstrate how the non-differentiabiliy prevents us from using the analytical gradient, and how our control-variate approach can pass low-variance gradient estimations through the classic solver and the discrete allocation space.

IV-C 1 Gradient

𝜃 {\frac{\partial\mu^{*}}{\partial\theta}} divide start_ARG ∂ italic_μ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT end_ARG start_ARG ∂ italic_θ end_ARG , the optimization process in g ⁢ ( ⋅ ) 𝑔 ⋅ g(\cdot) italic_g ( ⋅ ) is not differentiable; and (iii) μ ∗ superscript 𝜇 \mu^{*} italic_μ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT and θ 𝜃 \theta italic_θ related implicitly. To deal with the non-differentiability, we can use the Log-derivative trick, which has been widely used in RL, and estimates the above gradient as

However, our experiments showed that this estimator provides a gradient with a high variance, which slows down the convergence rate and compromises the solution quality.

IV-C 2 Control Variate

To address the above issue, we introduce a control variate  [ 28 ] to reduce the variance of a stochastic estimator. Suppose d 𝑑 d italic_d (as in derivative) is a random variable (RV), h ⁢ ( d ) ℎ 𝑑 h(d) italic_h ( italic_d ) is an estimator of 𝔼 ⁢ ( d ) 𝔼 𝑑 \mathbb{E}(d) blackboard_E ( italic_d ) , the control variate c ⁢ ( d ) 𝑐 𝑑 c(d) italic_c ( italic_d ) is a function of d 𝑑 d italic_d whose mean value is known. Define a new estimator with a control variate as:

When constant ζ 𝜁 \zeta italic_ζ is properly chosen, h ⁢ ( d ) n ⁢ e ⁢ w ℎ subscript 𝑑 𝑛 𝑒 𝑤 h(d)_{new} italic_h ( italic_d ) start_POSTSUBSCRIPT italic_n italic_e italic_w end_POSTSUBSCRIPT has the same expected value but lower variance than h ⁢ ( d ) ℎ 𝑑 h(d) italic_h ( italic_d ) , as long as the control variate c ⁢ ( d ) 𝑐 𝑑 c(d) italic_c ( italic_d ) is correlated to h ⁢ ( d ) ℎ 𝑑 h(d) italic_h ( italic_d ) . We briefly summarize the underlying principle of control variate technique  [ 45 ] as follows and omit the dependency on d 𝑑 d italic_d for simplicity.

ℎ 𝜁 𝑐 𝔼 𝑐 h_{new}=h+\zeta(c-\mathbb{E}(c)) italic_h start_POSTSUBSCRIPT italic_n italic_e italic_w end_POSTSUBSCRIPT = italic_h + italic_ζ ( italic_c - blackboard_E ( italic_c ) ) has same expected value but smaller variance, when the constant ζ 𝜁 \zeta italic_ζ is properly chosen and c 𝑐 c italic_c is correlated with h ℎ h italic_h .

The variance of the new estimator is

Differentiate the above equation w.r.t. γ 𝛾 \gamma italic_γ and set the derivative to zero, the optimal choice of ζ 𝜁 \zeta italic_ζ is

superscript 𝜁 2 Var 𝑐 2 𝜁 Cov ℎ 𝑐 0 \zeta^{2}\mathrm{Var}(c)+2\zeta\mathrm{Cov}(h,c)<0 italic_ζ start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT roman_Var ( italic_c ) + 2 italic_ζ roman_Cov ( italic_h , italic_c ) < 0 , we get ζ ∈ ( − 2 ⁢ C ⁢ o ⁢ v ⁢ ( h , c ) Var ⁢ ( c ) , 0 ) 𝜁 2 C o v ℎ 𝑐 Var 𝑐 0 \zeta\in(\frac{-2\mathrm{Cov}(h,c)}{\mathrm{Var}(c)},0) italic_ζ ∈ ( divide start_ARG - 2 roman_C roman_o roman_v ( italic_h , italic_c ) end_ARG start_ARG roman_Var ( italic_c ) end_ARG , 0 ) , which indicates that as long as k 𝑘 k italic_k is set in this range, Var ⁢ ( h new ) Var subscript ℎ new \mathrm{Var}(h_{\text{new}}) roman_Var ( italic_h start_POSTSUBSCRIPT new end_POSTSUBSCRIPT ) is less than Var ⁢ ( h ) Var ℎ \mathrm{Var}(h) roman_Var ( italic_h ) . When h ℎ h italic_h and c 𝑐 c italic_c are highly correlated and are of similar ranges, Cov ⁢ ( h , c ) ≈ Var ⁢ ( c ) Cov ℎ 𝑐 Var 𝑐 \mathrm{Cov}(h,c)\approx\mathrm{Var}(c) roman_Cov ( italic_h , italic_c ) ≈ roman_Var ( italic_c ) , thus ζ ∗ ≈ − 1 superscript 𝜁 1 \zeta^{*}\approx-1 italic_ζ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ≈ - 1 , which is our empirical choice of ζ 𝜁 \zeta italic_ζ .

Inspired by the control variant gradient estimator ( 10 ) we design a lower variance, unbiased gradient estimator using trainable surrogate network s 𝑠 s italic_s . Choose the allocation log-derivative estimator as h ⁢ ( d ) ℎ 𝑑 h(d) italic_h ( italic_d ) in ( 10 ), and replace c ⁢ ( d ) 𝑐 𝑑 c(d) italic_c ( italic_d ) and 𝔼 ⁢ [ c ⁢ ( d ) ] 𝔼 delimited-[] 𝑐 𝑑 \mathbb{E}[c(d)] blackboard_E [ italic_c ( italic_d ) ] with the surrogate log-derivative estimator and the actual surrogate network gradient, respectively, the upper-level costs U θ subscript 𝑈 𝜃 U_{\theta} italic_U start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT of our bilevel framework is:

where the constant ζ 𝜁 \zeta italic_ζ in ( 10 ) is substituted with − 1 1 -1 - 1 . L ′ superscript 𝐿 ′ L^{\prime} italic_L start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT is output of the surrogate network (control variate) but is taken as a constant by cutting its gradients. In turn, our gradient for the allocation network parameters θ 𝜃 \theta italic_θ is:

IV-C 3 Surrogate Network

We implement the idea of control variate with a surrogate network s ⁢ ( γ ) 𝑠 𝛾 s(\gamma) italic_s ( italic_γ ) in parallel with the TSP solver. Note that the surrogate network takes the allocation matrix P 𝑃 P italic_P as its input and predicts the maximum tour length, while the inputs of the actual TSP solver are allocations A 𝐴 A italic_A and coordinate data X 𝑋 X italic_X . Naively optimizing the surrogate network to imitate the input-output map of the TSP solver is ineffective because learning such a map does not guarantee learning correct gradient information. Since we require the surrogate network (control variate) to reduce the gradient variance of allocation parameters, we directly optimize the surrogate parameters to minimize a single sample estimation of the allocation gradient variance. Thus, the upper-level objective U γ subscript 𝑈 𝛾 U_{\gamma} italic_U start_POSTSUBSCRIPT italic_γ end_POSTSUBSCRIPT for the surrogate network is

𝜃 2 \rm{Var}(\frac{\partial U_{\theta}}{\partial\theta})=\mathbb{E}[(\frac{% \partial U_{\theta}}{\partial\theta})^{2}]-\mathbb{E}[(\frac{\partial U_{% \theta}}{\partial\theta})]^{2} roman_Var ( divide start_ARG ∂ roman_U start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT end_ARG start_ARG ∂ italic_θ end_ARG ) = blackboard_E [ ( divide start_ARG ∂ roman_U start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT end_ARG start_ARG ∂ italic_θ end_ARG ) start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT ] - blackboard_E [ ( divide start_ARG ∂ roman_U start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT end_ARG start_ARG ∂ italic_θ end_ARG ) ] start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT , the gradient of the surrogate network is

𝜃 2 \frac{\partial}{\partial\gamma}\mathbb{E}[(\frac{\partial U_{\theta}}{\partial% \theta})^{2}] divide start_ARG ∂ end_ARG start_ARG ∂ italic_γ end_ARG blackboard_E [ ( divide start_ARG ∂ italic_U start_POSTSUBSCRIPT italic_θ end_POSTSUBSCRIPT end_ARG start_ARG ∂ italic_θ end_ARG ) start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT ] is always zero because the surrogate network has no explicit influence on the return L 𝐿 L italic_L . For ease of understanding, we summarize our control variate-based bilevel optimization method in Algorithm 1 .

V Experiments

We next conduct comprehensive experiments to demonstrate the generalization ability, computational efficiency, and convergence speed of our iMTSP framework. We focus our experiments on large-scale settings ( ≥ 400 absent 400 \geq 400 ≥ 400 cities) because current classic solvers can already efficiently find near-optimal solutions for small-scale problems.

V-A Baselines

To demonstrate the advantages of our method, we compare it with both classic methods and learning-based methods. Specifically, we select a state-of-the-art reinforcement learning (RL)-based model from  [ 14 ] as a baseline. Their framework can efficiently solve MTSPs with up to a few thousand cities. Using S-batched REINFORCE, it has shown outstanding generalization ability and has a reduced variance for the gradient estimator than the vanilla REINFORCE  [ 23 ] . The other potential baseline methods  [ 13 , 46 , 20 ] either don’t provide source codes or cannot be directly applied to our settings. We also compare iMTSP with a well-known meta-heuristic method implemented by the Google OR-Tools routing library  [ 18 , 22 , 14 ] . It provides near-optimal solutions to MTSPs with a few hundred cities and is a popular MTSP baseline  [ 29 ] . For abbreviation, we will refer to the two methods as an RL baseline and Google OR-Tools. All approaches are tested locally with the same hardware.

V-B Experiment Setting

We learn from  [ 17 , 22 , 18 ] that, existing classic and learning-based approaches can handle MTSPs with about 150 150 150 150 cities, but their performance will significantly compromise with 400 400 400 400 or more cities. To demonstrate iMTSP’s ability to generalization and handle large-scale problems, we conduct experiments on training sets with 50 50 50 50 to 100 100 100 100 cities but test the models on problems with 400 400 400 400 to 1000 1000 1000 1000 cities. We believe this challenging setting can reflect the generalization ability of the proposed models.

In our tests, all the instances are generated by uniformly sampling N 𝑁 N italic_N coordinates in a unit rectangular so that both x 𝑥 x italic_x and y 𝑦 y italic_y coordinates are in the range of 0 0 to 1 1 1 1 . We employ a batch size of 512 512 512 512 and a training-to-validation data size ratio of 10 : 1 : 10 1 10:1 10 : 1 . The test set consists of i.i.d. batches but with a larger number of cities ( 400 400 400 400 to 1000 1000 1000 1000 ) as aforementioned.

Specifically, agents and cities are embedded into 64 64 64 64 dimensional vectors. The allocation network contains one attention layer, where keys, queries, and values are of 128 128 128 128 , 16 16 16 16 , and 16 16 16 16 dimensions, respectively. The clip constant α 𝛼 \alpha italic_α in ( 6c ) is set to be 10 10 10 10 . The surrogate network consists of three fully connected layers, whose hidden dimension is 256 256 256 256 and activation function is tanh . Google OR-Tools provides the TSP solver in iMTSP and the MTSP solver as a baseline. It uses the “Global Cheapest Arc” strategy to generate its initial solutions and uses “Guided local search” for local improvements. All the strategies are defined in  [ 29 ] and we selected the best options in the experiments.

V-C Quantitative Performance

We next conduct a quantitative performance comparison with the two baseline methods and show it in Table  I . We focus on large-scale MTSPs since many approaches can well solve small-size MTSPs but very few algorithms (both classic or learning-based) can deal with large-scale problems.

V-C 1 Comparison with Google OR-Tools

By decomposing a large MTSP into several small TSPs, iMTSP is stronger to handle large-scale problems. We demonstrate such a merit by comparing our model with the classic routing module in OR-Tools, which is given 300 300 300 300 seconds time budget. The results are shown in Table I . Specially, these route lengths of OR-Tools are averaged over 10 10 10 10 test instances. OR-Tools appears to be very inferior because it cannot converge to a local minimum given 300 300 300 300 seconds time budget. In our experiments, OR-Tools can handle 500 500 500 500 or less cities with 1800 1800 1800 1800 seconds budget. However, it does not converge even computing for 7200 7200 7200 7200 seconds with 600 600 600 600 or more cities, indicating that its computational complexity grows steeply w.r.t. the problem size. Also, the difference of the route length increases as the problem size becomes larger and larger. Remember that the final routes of iMTSP are also solved by Google routing module, while it can easily handle MTSP with up to a few thousand cities with the help of the allocation network.

V-C 2 Comparison with the RL Baseline

To show the effectiveness of our control variate-based optimization algorithm, we also compare iMTSP with the RL baseline  [ 14 ] which shares a similar forward process as iMTSP. In most cases, training on bigger problems leads to a better generalization ability on large-scale problems, but it also indicates larger parameter space, more complicated gradient information, and longer training time. This makes the quality of the gradient very crucial. As presented in the Table  I , iMTSP outperforms the RL baseline in most cases, providing solutions with 3.2 ± 0.01 % plus-or-minus 3.2 percent 0.01 3.2\pm 0.01\% 3.2 ± 0.01 % shorter maximum route length over the RL baseline on average. When the models are trained with 100 100 100 100 cities, the difference between the route lengths monotonically increases from 0.4 % percent 0.4 0.4\% 0.4 % to 8.0 % percent 8.0 8.0\% 8.0 % and from 3.4 % percent 3.4 3.4\% 3.4 % to 8.9 % percent 8.9 8.9\% 8.9 % , respectively with 10 10 10 10 and 15 15 15 15 agents. The results demonstrate that with the lower-variance gradient provided by our control variate-based optimization algorithm, iMTSP usually converges to better solutions when being trained on large-scale instances.

V-D Qualitative Performance

To find out the specific advantages in iMTSP’s solutions, we plot and compare the results of iMTSP and two baselines on two example instances. Fig.  2 provides a visualization of the solutions from both baselines and iMTSP on two instances with 5 5 5 5 agents and 500 500 500 500 cities. The depot of the first instance is close to the center of cities while it’s off the center in the second instance. In Fig.  2(d) , there are long straight partial routes (e.g., blue and purple), indicating some agents have travelled for a long distance before they visit their first destination. Also, some circular parts exist in the OR-Tools’ solutions (e.g., the green route in Fig.  2(b) ) meaning that this agent travels for extra distance to visit the cities on the circle. Both of these are typical symptoms of sub-optimality. Such symptoms are not observed in the two solutions from iMTSP. In both instances, iMTSP produces the best performance. Note that both the RL baseline and iMTSP finish their computation within a few seconds while OR-Tools takes 1800 1800 1800 1800 seconds to produce comparable solutions.

V-E Efficiency Analysis

Since iMTSP contains both a learning-based allocation network and a classic TSP solver, it is important to identify the bottleneck of the architecture for future improvements. As in Table II , with 5 5 5 5 , 10 10 10 10 , and 15 15 15 15 agents, the computing time of our model are 4.85 4.85 4.85 4.85 seconds, 1.98 1.98 1.98 1.98 seconds, and 1.35 1.35 1.35 1.35 seconds, respectively, to solve one instance with 1000 1000 1000 1000 cities. Note that the computing time decrease as the number of agents increases. This fact indicates that the major computational bottleneck is the TSP solvers rather than the allocation network, because more agents are required to run more times of TSP solvers. One of the promising solutions to further reduce our computing time is to create multiple threads to run the TSP solvers in parallel since the TSPs in the lower-level optimization of iMSTP are independent. Since this is not the focus of this paper, we put it as a future work.

V-F Gradient Variance

As demonstrated in Section  IV-C , with an optimized surrogate network, the variance of iMTSP’s gradient are expected to be smaller than the gradient from the vanilla REINFORCE algorithm  [ 23 ] . We verify such a hypothesis by explicitly recording the mini-batch gradient variance during the training process. The experiment is conducted twice with 10 10 10 10 agents visiting 50 50 50 50 cities and 100 100 100 100 cities. Training data are divided into several mini-batches, each of which contains 32 32 32 32 instances. The gradient is computed and stored for every mini-batch, and the variance is later computed with these stored gradient. The network parameters are updated with the average gradient of the whole batch. The results are shown in Fig.  3 , where the x 𝑥 x italic_x -axis denotes the number of iterations and the y 𝑦 y italic_y -axis represents the natural logarithm of the summed variance of all trainable parameters in the allocation network. It is observed that the gradient variance of our iMTSP is much smaller and converges 20 × 20\times 20 × faster than the RL baseline. This verifies the effectiveness of our control variate-based bilevel optimization process.

V-G Ablation Study

To confirm that the improvements of solution quality are majorly contributed by the control variate-based optimization algorithm, we also track the performance of the fine-tuned network with the baseline optimization method. As shown in Table III , the route lengths from our control variate-based optimization algorithm are averagely 7.8 % ± 2.1 % plus-or-minus percent 7.8 percent 2.1 7.8\%\pm 2.1\% 7.8 % ± 2.1 % shorter than that from the baseline algorithm. We can also observe that better results always come from iMTSP, which indicates that the better solution quality is mainly contributed by our control variate-based optimization algorithm.

VI Conclusion and Future Work

In the paper, we reformulate the Min-Max MTSP as a bilevel optimization problem. We introduce a self-supervised framework iMTSP, which can efficiently handle large-scale MTSP with thousands of cities. With the control variate-based optimization algorithm, iMTSP produces a low-variance gradient through a non-differentiable TSP solver and a discrete allocation space to update the allocation network. Experimental results demonstrated the advantages of iMTSP in solution quality, computational efficiency, and optimization stability. In future work, we will also consider the constraints of environmental obstacles and inter-agent collision, which will enable iMTSP to conduct multi-agent path planning in real-world scenarios.

VII Acknowledgements

This work was, in part, funded by the DARPA grant DARPA-PS-23-13. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of DARPA.

• [1] K. Sundar and S. Rathinam, “Algorithms for routing an unmanned aerial vehicle in the presence of refueling depots,” IEEE Transactions on Automation Science and Engineering , vol. 11, no. 1, pp. 287–294, 2013.
• [2] Y. Ma, H. Zhang, Y. Zhang, R. Gao, Z. Xu, and J. Yang, “Coordinated optimization algorithm combining GA with cluster for multi-UAVs to multi-tasks task assignment and path planning,” in International Conference on Control and Automation .   IEEE, 2019, pp. 1026–1031.
• [3] R. F. Carpio, J. Maiolini, C. Potena, E. Garone, G. Ulivi, and A. Gasparn, “Mp-stsp: A multi-platform steiner traveling salesman problem formulation for precision agriculture in orchards,” in International Conference on Robotics and Automation .   IEEE, 2021, pp. 2345–2351.
• [4] Z. Ren, S. Rathinam, and H. Choset, “CBSS: A new approach for multiagent combinatorial path finding,” IEEE Transactions on Robotics , vol. 39, no. 4, pp. 2669–2683, 2023.
• [5] T. Bektas, “The multiple traveling salesman problem: an overview of formulations and solution procedures,” omega , vol. 34, no. 3, pp. 209–219, 2006.
• [6] E. Gaztañaga, “The mass of our observable universe,” Monthly Notices of the Royal Astronomical Society: Letters , vol. 521, no. 1, pp. L59–L63, 2023.
• [7] J. Park, C. Kwon, and J. Park, “Learn to solve the min-max multiple traveling salesmen problem with reinforcement learning,” in Proceedings of the 2023 International Conference on Autonomous Agents and Multiagent Systems , 2023, pp. 878–886.
• [8] A. M. Ham, “Integrated scheduling of m-truck, m-drone, and m-depot constrained by time-window, drop-pickup, and m-visit using constraint programming,” Transportation Research Part C: Emerging Technologies , vol. 91, pp. 1–14, 2018.
• [9] Z. Ren, S. Rathinam, and H. Choset, “MS: A new exact algorithm for multi-agent simultaneous multi-goal sequencing and path finding,” in International Conference on Robotics and Automation .   IEEE, 2021, pp. 11 560–11 565.
• [10] K. Bérczi, M. Mnich, and R. Vincze, “Approximations for many-visits multiple traveling salesman problems,” Omega , vol. 116, p. 102816, 2023.
• [11] M. A. Al-Omeer and Z. H. Ahmed, “Comparative study of crossover operators for the MTSP,” in 2019 International Conference on Computer and Information Sciences .   IEEE, 2019, pp. 1–6.
• [12] R. Necula, M. Breaban, and M. Raschip, “Tackling the bi-criteria facet of multiple traveling salesman problem with ant colony systems,” in 27th International Conference on Tools with Artificial Intelligence .   IEEE, 2015, pp. 873–880.
• [13] H. Liang, Y. Ma, Z. Cao, T. Liu, F. Ni, Z. Li, and J. Hao, “SplitNet: a reinforcement learning based sequence splitting method for the MinMax multiple travelling salesman problem,” in Proceedings of the AAAI Conference on Artificial Intelligence , vol. 37, no. 7, 2023, pp. 8720–8727.
• [14] Y. Hu, Y. Yao, and W. S. Lee, “A reinforcement learning approach for optimizing multiple traveling salesman problems over graphs,” Knowledge-Based Systems , vol. 204, p. 106244, 2020.
• [15] L. Xin, W. Song, Z. Cao, and J. Zhang, “NeuroLKH: Combining deep learning model with Lin-Kernighan-Helsgaun heuristic for solving the traveling salesman problem,” Advances in Neural Information Processing Systems , vol. 34, pp. 7472–7483, 2021.
• [16] S. Miki, D. Yamamoto, and H. Ebara, “Applying deep learning and reinforcement learning to traveling salesman problem,” in International Conference on Computing, Electronics and Communications Engineering .   IEEE, 2018, pp. 65–70.
• [17] O. Vinyals, M. Fortunato, and N. Jaitly, “Pointer networks,” Advances in Neural Information Processing Systems , vol. 28, 2015.
• [18] W. Kool, H. Van Hoof, and M. Welling, “Attention, learn to solve routing problems!” arXiv preprint arXiv:1803.08475 , 2018.
• [19] M. Nazari, A. Oroojlooy, L. Snyder, and M. Takác, “Reinforcement learning for solving the vehicle routing problem,” Advances in Neural Information Processing Systems , vol. 31, 2018.
• [20] J. Park, S. Bakhtiyar, and J. Park, “Schedulenet: Learn to solve multi-agent scheduling problems with reinforcement learning,” arXiv preprint arXiv:2106.03051 , 2021.
• [21] E. Khalil, H. Dai, Y. Zhang, B. Dilkina, and L. Song, “Learning combinatorial optimization algorithms over graphs,” Advances in Neural Information Processing Systems , vol. 30, 2017.
• [22] Y. Wu, W. Song, Z. Cao, J. Zhang, and A. Lim, “Learning improvement heuristics for solving routing problems,” IEEE Transactions on Neural Networks and Learning Systems , vol. 33, no. 9, pp. 5057–5069, 2021.
• [23] R. J. Williams, “Simple statistical gradient-following algorithms for connectionist reinforcement learning,” Machine Learning , vol. 8, pp. 229–256, 1992.
• [24] T. Fu, S. Su, Y. Lu, and C. Wang, “iSLAM: Imperative SLAM,” IEEE Robotics and Automation Letters (RA-L) , 2024.
• [25] F. Yang, C. Wang, C. Cadena, and M. Hutter, “iPlanner: Imperative path planning,” in Robotics: Science and Systems (RSS) , 2023.
• [26] Z. Zhan, D. Gao, Y.-J. Lin, Y. Xia, and C. Wang, “iMatching: Imperative correspondence learning,” arXiv preprint arXiv:2312.02141 , 2023.
• [27] M. Figurnov, S. Mohamed, and A. Mnih, “Implicit reparameterization gradients,” Advances in Neural Information Processing Systems , vol. 31, 2018.
• [28] B. L. Nelson, “Control variate remedies,” Operations Research , vol. 38, no. 6, pp. 974–992, 1990.
• [29] L. Perron and F. Didier, “ORTools routing options,” Google, 2023. [Online]. Available: https://developers.google.com/optimization/routing/routing_options
• [30] O. Cheikhrouhou and I. Khoufi, “A comprehensive survey on the multiple traveling salesman problem: Applications, approaches and taxonomy,” Computer Science Review , vol. 40, p. 100369, 2021.
• [31] C. Wei, Z. Ji, and B. Cai, “Particle swarm optimization for cooperative multi-robot task allocation: a multi-objective approach,” IEEE Robotics and Automation Letters , vol. 5, no. 2, pp. 2530–2537, 2020.
• [32] P. Kitjacharoenchai, M. Ventresca, M. Moshref-Javadi, S. Lee, J. M. Tanchoco, and P. A. Brunese, “Multiple traveling salesman problem with drones: Mathematical model and heuristic approach,” Computers and Industrial Engineering , vol. 129, pp. 14–30, 2019.
• [33] C. C. Murray and R. Raj, “The multiple flying sidekicks traveling salesman problem: Parcel delivery with multiple drones,” Transportation Research Part C: Emerging Technologies , vol. 110, pp. 368–398, 2020.
• [34] D. E. Rumelhart, G. E. Hinton, R. J. Williams et al. , “Learning internal representations by error propagation,” 1985.
• [35] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin, “Attention is all you need,” Advances in Neural Information Processing Systems , vol. 30, 2017.
• [36] E. Greensmith, P. L. Bartlett, and J. Baxter, “Variance reduction techniques for gradient estimates in reinforcement learning.” Journal of Machine Learning Research , vol. 5, no. 9, 2004.
• [37] W. Grathwohl, D. Choi, Y. Wu, G. Roeder, and D. Duvenaud, “Backpropagation through the void: Optimizing control variates for black-box gradient estimation,” arXiv preprint arXiv:1711.00123 , 2017.
• [38] S. S. Gu, T. Lillicrap, R. E. Turner, Z. Ghahramani, B. Schölkopf, and S. Levine, “Interpolated policy gradient: Merging on-policy and off-policy gradient estimation for deep reinforcement learning,” Advances in Neural Information Processing Systems , vol. 30, 2017.
• [39] H. Liu, R. Socher, and C. Xiong, “Taming MAML: Efficient unbiased meta-reinforcement learning,” in International Conference on Machine Learning .   PMLR, 2019, pp. 4061–4071.
• [40] S. P. Karimireddy, S. Kale, M. Mohri, S. Reddi, S. Stich, and A. T. Suresh, “Scaffold: Stochastic controlled averaging for federated learning,” in International Conference on Machine Learning .   PMLR, 2020, pp. 5132–5143.
• [41] J. Baker, P. Fearnhead, E. B. Fox, and C. Nemeth, “Control variates for stochastic gradient MCMC,” Statistics and Computing , vol. 29, pp. 599–615, 2019.
• [42] T. Geffner and J. Domke, “Using large ensembles of control variates for variational inference,” Advances in Neural Information Processing Systems , vol. 31, 2018.
• [43] W. Guo, S. Wang, P. Ding, Y. Wang, and M. I. Jordan, “Multi-source causal inference using control variates,” arXiv preprint arXiv:2103.16689 , 2021.
• [44] J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, and G. E. Dahl, “Neural message passing for quantum chemistry,” in International Conference on Machine Learning .   PMLR, 2017, pp. 1263–1272.
• [45] S. Meyn, Control techniques for complex networks .   Cambridge University Press, 2008.
• [46] H. Gao, X. Zhou, X. Xu, Y. Lan, and Y. Xiao, “AMARL: An attention-based multiagent reinforcement learning approach to the min-max multiple traveling salesmen problem,” IEEE Transactions on Neural Networks and Learning Systems , 2023.

Solving the Traveling Salesman Problem for Efficient Route Planning Through Swarm Intelligence Based Optimization

• Conference paper
• First Online: 21 August 2024
• Cite this conference paper

• Frederick Kin Hing Phoa   ORCID: orcid.org/0000-0002-7417-8982 9 &
• Kin To Wong 10  

Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 14789))

Included in the following conference series:

• International Conference on Swarm Intelligence

72 Accesses

The Traveling Salesman Problem (TSP) has long been a challenging optimization puzzle, prompting the development of various methodologies to seek efficient solutions. In this paper, we propose an improved method utilizing a Swarm Intelligence-based approach. Besides the traditional MIX and MOVE operations, our major contribution lies in the introduction of a new MIX operation specifically tailored for the TSP. This new operation offers an advantage over the traditional MIX operation by providing more comprehensive domain exploration. We compare our improved method to conventional optimization techniques, namely the Genetic Algorithm and Ant Colony Optimization. For a TSP involving 50 popular U.S. landmarks, our proposed method outperforms the others in terms of solution quality and computational time. Results are visualized on maps for reference.

This work is partially supported by the Academia Sinica grant number AS-IA-112-M03 and the National Science and Technology Council (Taiwan) grant number 111-2118-M-001-007-MY2.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Subscribe and save.

• Get 10 units per month
• Download Article/Chapter or eBook
• 1 Unit = 1 Article or 1 Chapter
• Cancel anytime
• Available as PDF
• Read on any device
• Instant download
• Own it forever
• Available as EPUB and PDF
• Compact, lightweight edition
• Dispatched in 3 to 5 business days
• Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Flood, M.M.: The traveling-salesman problem. Oper. Res. 4 (1), 61–75 (1956)

Article   Google Scholar  

Hoffman, K.L., Padberg, M., Rinaldi, G.: Traveling salesman problem. Encycl. Oper. Res. Manag. Sci. 1 , 1573–1578 (2013)

Google Scholar  

Miller, C., Tucker, A.W., Zemlin, R.A.: Integer programming formulation of traveling salesman problems. J. ACM 7 (4), 326–329 (1960)

Article   MathSciNet   Google Scholar  

Bellman, R.: Dynamic programming treatment of the travelling salesman problem. J. ACM 9 (1), 61–63 (1962)

Rosenkrantz, D.J., Stearns, R.E., Lewis, P.: An analysis of several heuristics for the traveling salesman problem. SIAM J. Comput. 6 (3), 563–581 (1977)

Reinelt, G.: TSPLIB - a traveling salesman problem library. ORSA J. Comput. 3 (4), 376–384 (1991)

Jiang, H., He, Z., Ye, G., Zhang, H.: Network intrusion detection based on PSO-XGBoost model. IEEE Access 8 , 58392–58401 (2020)

Phoa, F.K.H., Chen, R.B., Wang, W.C., Wong, W.K.: Optimizing two-level supersaturated designs using swarm intelligence techniques. Technometrics 58 (1), 43–49 (2016)

Phoa, F.K.H.: A Swarm Intelligence Based (SIB) method for optimization in designs of experiments. Nat. Comput. 16 (4), 597–605 (2017)

Lin, F.P.C., Phoa, F.K.H.: An efficient construction of confidence regions via swarm intelligence and its application in target localization. IEEE Access 6 , 8610–8618 (2017)

Lin, F.P.C., Phoa, F.K.H.: Runtime estimation and scheduling on parallel processing super-computers via instance-based learning and swarm intelligence. Int. J. Mach. Learn. Comput. 9 , 592–598 (2019)

Hsu, T.-C., Phoa, F.K.H.: A smart initialization on the swarm intelligence based method for efficient search of optimal minimum energy design. In: Tan, Y., Shi, Y., Tang, Q. (eds.) ICSI 2018. LNCS, vol. 10941, pp. 78–87. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-93815-8_9

Chapter   Google Scholar  

Phoa, F.K.H., Liu, H.-P., Chen-Burger, Y.-H.J., Lin, S.-P.: Metaheuristic optimization on tensor-type solution via swarm intelligence and its application in the profit optimization in designing selling scheme. In: Tan, Y., Shi, Y. (eds.) ICSI 2021. LNCS, vol. 12689, pp. 72–82. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-78743-1_7

Liu, H.P., Phoa, F.K.H., Chen-Burger, Y.H., Lin, S.P.: An efficient swarm intelligence approach to the optimization on high-dimensional solutions with cross-dimensional constraints with applications in supply chain management. Front. Comput. Neurosci. 18 , 1283974 (2024)

Sun, W.H., Phoa, F.K.H.: Network community detection via an improved swarm intelligence approach. In: Tan, Y., Shi, Y., Niu, B. (eds.) Advances in Swarm Intelligence, vol. 13344, pp. 419–431. Springer, Cham (2022). https://doi.org/10.1007/978-3-031-09677-8_35

Huang, E.C.H., Phoa, F.K.H.: A uniform placement of alters on spherical surface (U-PASS) for ego-centric networks with community structure and alter attributes. Adv. Complex Syst. 26 , 2340003 (2023)

Sutrisno, H., Phoa, F.K.H.: Anomalous subsequence detection in time series: mathematical formulation and a novel evolutionary algorithm based on clustering and swarm intelligence. Appl. Intell. 53 , 29585–29603 (2023)

Yen, P.-C., Phoa, F.K.H.: Traveling salesman problem via swarm intelligence. In: Tan, Y., Shi, Y. (eds.) ICSI 2021. LNCS, vol. 12689, pp. 106–115. Springer, Cham (2021). https://doi.org/10.1007/978-3-030-78743-1_10

Olson, R.S.: Computing the optimal road trip across the U.S. (2015)

Download references

Acknowledgement

Wong is supported by the master student scholarship provided by the Institute of Statistical Science, Academia Sinica. Part of this work was a version included in the master thesis of Mr. Kin To Wong.

Author information

Authors and affiliations.

Institute of Statistical Science, Academia Sinica, Taipei, 115, Taiwan

Frederick Kin Hing Phoa

Data Science Degree Program, National Taiwan University, Taipei, 106, Taiwan

Kin To Wong

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Frederick Kin Hing Phoa .

Editor information

Editors and affiliations.

Peking University, Beijing, China

Southern University of Science and Technology, Shenzhen, China

Rights and permissions

Reprints and permissions

Copyright information

© 2024 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.

About this paper

Cite this paper.

Phoa, F.K.H., Wong, K.T. (2024). Solving the Traveling Salesman Problem for Efficient Route Planning Through Swarm Intelligence Based Optimization. In: Tan, Y., Shi, Y. (eds) Advances in Swarm Intelligence. ICSI 2024. Lecture Notes in Computer Science, vol 14789. Springer, Singapore. https://doi.org/10.1007/978-981-97-7184-4_1

Download citation

DOI : https://doi.org/10.1007/978-981-97-7184-4_1

Published : 21 August 2024

Publisher Name : Springer, Singapore

Print ISBN : 978-981-97-7183-7

Online ISBN : 978-981-97-7184-4

eBook Packages : Computer Science Computer Science (R0)

Share this paper

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Publish with us

Policies and ethics

• Find a journal
• Track your research