knight's tour 10x10

ç Knight's Tour Notes Index

Knight's Tours of the 10×10 Board

Historical examples, examples of my own work, the enumeration of 10 by 10 knight's tours with quaternary symmetry, 10×10 board: semi-magic tour.

• Mission and Vision
• Annual Reports
• Complaints Procedures
• Delegates Information
• 2024 Delegates Call
• Executive Board
• Staff/Contact Us
• Requests for Proposals (RFP)
• Job Postings
• Guide to a Successful Chess Club
• The Ratings System
• New to National Events Guide
• Safe Play Policy
• How to Send an Email Blast
• Guide to Scholastic Chess
• Accessibility Guidelines
• Our Initiative
• Top 100 Lists
• Olympiad Campaign
• At-Risk Youth
• Correspondence Chess
• 2023-24 Scholastic Regulations
• Scholastic Council Members
• Chess Life Kids Online
• Faces of US Chess
• Our Heritage: Yearbook
• Upcoming Events
• Grants/Awards
• Spectator Policy at Scholastics
• Current Scholastic Regulations
• Event Bidding
• Official Rules
• Plan Ahead Calendar
• Grand Prix Information
• Pan American Youth Championships
• Pan Am Youth Champ
• Irwin: Seniors (50+)
• Denker: HS (9-12)
• Haring: Girls (K-12)
• Barber: MS (6-8)
• Rockefeller: ES (K-5)
• Weeramantry: Blitz
• Opening and Closing Ceremony Program
• Player/Ratings Look-Up
• Past Event Crosstables
• Events Rated List
• TD/Affiliate Support
• Club/Affiliate Search
• Rating System Algorithm
• MSA/Ratings FAQ
• Become a Member
• Become an Affiliate
• Redeem a Voucher
• Benefactor Members
• Membership Form PDF
• Info for Members/Affiliates
• Donor Bill of Rights
• Giving Tuesday
• Donate Online
• Case for Support
• At-Risk-Youth

Chess and Math: A Closer Look at the Knight's Tour

• August 2024 (11)
• July 2024 (44)
• June 2024 (27)
• May 2024 (32)
• April 2024 (51)
• March 2024 (34)
• February 2024 (25)
• January 2024 (26)
• December 2023 (29)
• November 2023 (26)
• October 2023 (37)
• September 2023 (27)
• August 2023 (37)
• July 2023 (47)
• June 2023 (33)
• May 2023 (37)
• April 2023 (45)
• March 2023 (37)
• February 2023 (28)
• January 2023 (31)
• December 2022 (23)
• November 2022 (32)
• October 2022 (31)
• September 2022 (19)
• August 2022 (39)
• July 2022 (32)
• June 2022 (35)
• May 2022 (21)
• April 2022 (31)
• March 2022 (33)
• February 2022 (21)
• January 2022 (27)
• December 2021 (36)
• November 2021 (34)
• October 2021 (25)
• September 2021 (25)
• August 2021 (41)
• July 2021 (36)
• June 2021 (29)
• May 2021 (29)
• April 2021 (31)
• March 2021 (33)
• February 2021 (28)
• January 2021 (29)
• December 2020 (38)
• November 2020 (40)
• October 2020 (41)
• September 2020 (35)
• August 2020 (38)
• July 2020 (36)
• June 2020 (46)
• May 2020 (42)
• April 2020 (37)
• March 2020 (60)
• February 2020 (39)
• January 2020 (45)
• December 2019 (35)
• November 2019 (35)
• October 2019 (42)
• September 2019 (45)
• August 2019 (56)
• July 2019 (44)
• June 2019 (35)
• May 2019 (40)
• April 2019 (48)
• March 2019 (61)
• February 2019 (39)
• January 2019 (30)
• December 2018 (29)
• November 2018 (51)
• October 2018 (45)
• September 2018 (29)
• August 2018 (49)
• July 2018 (35)
• June 2018 (31)
• May 2018 (39)
• April 2018 (31)
• March 2018 (26)
• February 2018 (33)
• January 2018 (30)
• December 2017 (26)
• November 2017 (24)
• October 2017 (30)
• September 2017 (30)
• August 2017 (32)
• July 2017 (27)
• June 2017 (32)
• May 2017 (26)
• April 2017 (37)
• March 2017 (28)
• February 2017 (30)
• January 2017 (27)
• December 2016 (29)
• November 2016 (24)
• October 2016 (32)
• September 2016 (31)
• August 2016 (27)
• July 2016 (24)
• June 2016 (26)
• May 2016 (19)
• April 2016 (30)
• March 2016 (37)
• February 2016 (27)
• January 2016 (33)
• December 2015 (25)
• November 2015 (23)
• October 2015 (16)
• September 2015 (28)
• August 2015 (28)
• July 2015 (6)
• June 2015 (1)
• May 2015 (2)
• April 2015 (1)
• February 2015 (3)
• January 2015 (1)
• December 2014 (1)
• July 2010 (1)
• October 1991 (1)
• August 1989 (1)
• January 1988 (1)
• December 1983 (1)

Announcements

• 2024 Olympiad Teams Announced »
• US Chess Seeks Marketing/Communications Manager »
• 2024 US Chess Awards Recipients »
• 2024 Delegates Call »

US CHESS PRESS

The Knight’s Tour

The  knight’s tour problem  is the mathematical problem of finding a knight’s tour, and probably making knight the most interesting piece on the chess board. The knight visits every square exactly once, if the knight ends on a square that is one knight’s move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed; otherwise, it is open.

The knight’s tour problem is an instance of the more general Hamiltonian path problem in graph theory. The problem of finding a closed knight’s tour is similarly an instance of the Hamiltonian cycle problem. Unlike the general Hamiltonian path problem, the knight’s tour problem can be solved in linear time.

Hamiltonian Path Problem

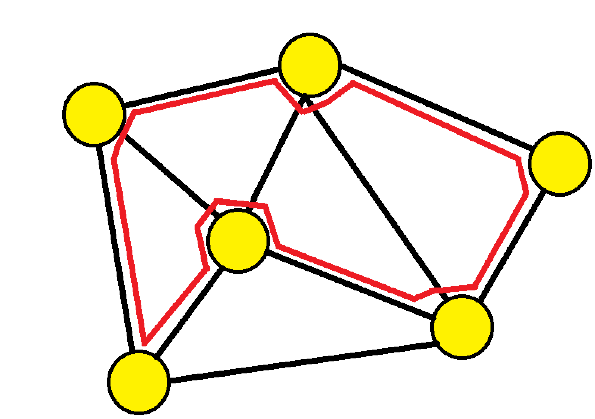
In Graph Theory, a graph is usually defined to be a collection of nodes or vertices and the set of edges which define which nodes are connected with each other. So we use a well known notation of representing a graph G = (V,E) where  V = { v 1 , v 2 , v 3 , … , v n }  and E = {(i, j)|i ∈ V and j ∈ V and i and j is connected}.

Hamiltonian Path is defined to be a single path that visits every node in the given graph, or a permutation of nodes in such a way that for every adjacent node in the permutation there is an edge defined in the graph. Notice that it does not make much sense in repeating the same paths. In order to avoid this repetition, we permute with |V| C 2 combinations of starting and ending vertices.

Simple way of solving the Hamiltonian Path problem would be to permutate all possible paths and see if edges exist on all the adjacent nodes in the permutation. If the graph is a complete graph, then naturally all generated permutations would quality as a Hamiltonian path.

For example. let us find a Hamiltonian path in graph G = (V,E) where V = {1,2,3,4} and E = {(1,2),(2,3),(3,4)}. Just by inspection, we can easily see that the Hamiltonian path exists in permutation 1234. The given algorithm will first generate the following permutations based on the combinations: 1342 1432 1243 1423 1234 1324 2143 2413 2134 2314 3124 3214

The number that has to be generated is ( |V| C 2 ) (|V| – 2)!

Schwenk proved that for any  m  ×  n  board with  m  ≤  n , a closed knight’s tour is always possible  unless  one or more of these three conditions are met:

• m  and  n  are both odd
• m  = 1, 2, or 4
• m  = 3 and  n  = 4, 6, or 8.

Cull and Conrad proved that on any rectangular board whose smaller dimension is at least 5, there is a (possibly open) knight’s tour.

Neural network solutions

The neural network is designed such that each legal knight’s move on the chessboard is represented by a neuron. Therefore, the network basically takes the shape of the  knight’s graph  over an n×n chess board. (A knight’s graph is simply the set of all knight moves on the board)

Each neuron can be either “active” or “inactive” (output of 1 or 0). If a neuron is active, it is considered part of the solution to the knight’s tour. Once the network is started, each active neuron is configured so that it reaches a “stable” state if and only if it has exactly two neighboring neurons that are also active (otherwise, the state of the neuron changes). When the entire network is stable, a solution is obtained. The complete transition rules are as follows:

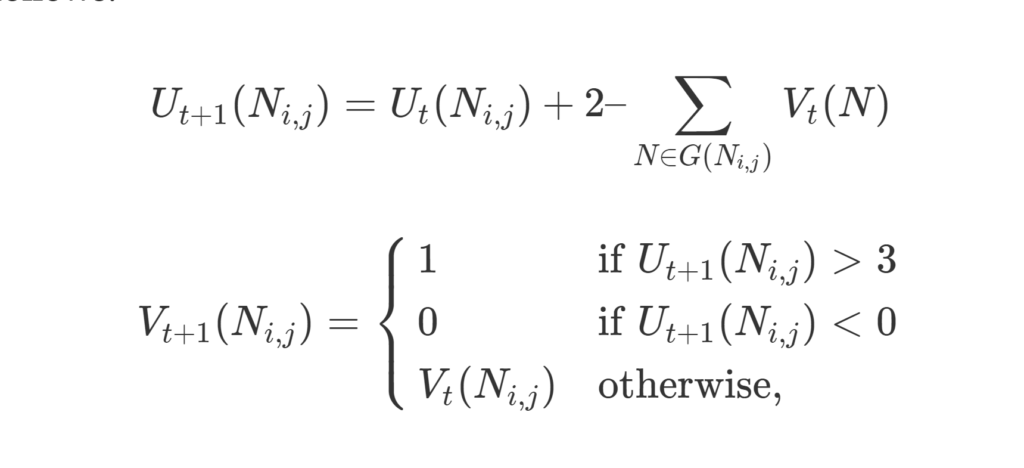
where t represents time (incrementing in discrete intervals), U(N i,j ) is the state of the neuron connecting square i to square j, V(N i,j ) is the output of the neuron from i to j, and G(N i,j ) is the set of “neighbors” of the neuron (all neurons that share a vertex with N i,j ).

Code For Knight’s Tour

You May Also Like

Möbius strip, the golden ratio, leave a reply cancel reply.

• A Knight’s Tour

The “ knight’s tour ” is a classic problem in graph theory, first posed over 1,000 years ago and pondered by legendary mathematicians including Leonhard Euler before finally being solved in 1823. We will use the knight’s tour problem to illustrate a second common graph algorithm called depth first search.

The knight’s tour puzzle is played on a chess board with a single chess piece, the knight. The object of the puzzle is to find a sequence of moves that allow the knight to visit every square on the board exactly once, like so:

One such sequence is called a “tour.” The upper bound on the number of possible legal tours for an eight-by-eight chessboard is known to be 1 . 3 0 5 × 1 0 3 5 1.305 \times 10^{35} 1 . 3 0 5 × 1 0 ​ 3 5 ​ ​ ; however, there are even more possible dead ends. Clearly this is a problem that requires some real brains, some real computing power, or both.

Once again we will solve the problem using two main steps:

• Represent the legal moves of a knight on a chessboard as a graph.
• Use a graph algorithm to find a path where every vertex on the graph is visited exactly once.

Building the Knight’s Tour Graph

To represent the knight’s tour problem as a graph we will use the following two ideas: Each square on the chessboard can be represented as a node in the graph. Each legal move by the knight can be represented as an edge in the graph.

We will use a Python dictionary to hold our graph, with the keys being tuples of coordinates representing the squares of the board, and the values being sets representing the valid squares to which a knight can move from that square.

To build the full graph for an n-by-n board we can use the Python function shown below. The build_graph function makes one pass over the entire board. At each square on the board the build_graph function calls a helper generator, legal_moves_from , to generate a list of legal moves for that position on the board. All legal moves are then made into undirected edges of the graph by adding the vertices appropriately to one anothers sets of legal moves.

The legal_moves_from generator below takes the position of the knight on the board and yields any of the eight possible moves that are still on the board.

The illustration below shows the complete graph of possible moves on an eight-by-eight board. There are exactly 336 edges in the graph. Notice that the vertices corresponding to the edges of the board have fewer connections (legal moves) than the vertices in the middle of the board. Once again we can see how sparse the graph is. If the graph was fully connected there would be 4,096 edges. Since there are only 336 edges, the adjacency matrix would be only 8.2 percent full.

Implementing Knight’s Tour

The search algorithm we will use to solve the knight’s tour problem is called depth first search ( DFS ). Whereas the breadth first search algorithm discussed in the previous section builds a search tree one level at a time, a depth first search creates a search tree by exploring one branch of the tree as deeply as possible.

The depth first exploration of the graph is exactly what we need in order to find a path that has exactly 63 edges. We will see that when the depth first search algorithm finds a dead end (a place in the graph where there are no more moves possible) it backs up the tree to the next deepest vertex that allows it to make a legal move.

The find_solution_for function takes just two arguments: a board_size argument and a heuristic function, which you should ignore for now but to which we will return.

It then constructs a graph using the build_graph function described above, and for each vertex in the graph attempts to traverse depth first by way of the traverse function.

The traverse function is a little more interesting. It accepts a path, as a list of coordinates, as well as the vertex currently being considered. If the traversal has proceeded deep enough that we know that every square has been visited once, then we return the full path traversed.

Otherwise, we use our graph to look up the legal moves from the current vertex, and exclude the vertices that we know have already been visited, to determine the vertices that are yet_to_visit . At this point we recursively call traverse with each of the vertices to visit, along with the path to reach that vertex including the current vertex. If any of the recursive calls return a path, then that path is the return value of the outer call, otherwise we return None.

Let’s look at a simple example of an equivalent of this traverse function in action.

It is remarkable that our choice of data structure and algorithm has allowed us to straightforwardly solve a problem that remained impervious to thoughtful mathematical investigation for centuries.

With some modification, the algorithm can also be used to discover one of a number of “closed” (circular) tours, which can therefore be started at any square of the board:

Knight’s Tour Analysis

There is one last interesting topic regarding the knight’s tour problem, then we will move on to the general version of the depth first search. The topic is performance. In particular, our algorithm is very sensitive to the method you use to select the next vertex to visit. For example, on a five-by-five board you can produce a path in about 1.5 seconds on a reasonably fast computer. But what happens if you try an eight-by-eight board? In this case, depending on the speed of your computer, you may have to wait up to a half hour to get the results! The reason for this is that the knight’s tour problem as we have implemented it so far is an exponential algorithm of size O ( k N ) O(k^N) O ( k ​ N ​ ​ ) , where N is the number of squares on the chess board, and k is a small constant. The diagram below can help us visualize why this is so.

The root of the tree represents the starting point of the search. From there the algorithm generates and checks each of the possible moves the knight can make. As we have noted before the number of moves possible depends on the position of the knight on the board. In the corners there are only two legal moves, on the squares adjacent to the corners there are three and in the middle of the board there are eight. The diagram below shows the number of moves possible for each position on a board. At the next level of the tree there are once again between 2 and 8 possible next moves from the position we are currently exploring. The number of possible positions to examine corresponds to the number of nodes in the search tree.

We have already seen that the number of nodes in a binary tree of height N is 2 N + 1 − 1 2^{N+1}-1 2 ​ N + 1 ​ ​ − 1 . For a tree with nodes that may have up to eight children instead of two the number of nodes is much larger. Because the branching factor of each node is variable, we could estimate the number of nodes using an average branching factor. The important thing to note is that this algorithm is exponential: k N + 1 − 1 k^{N+1}-1 k ​ N + 1 ​ ​ − 1 , where k k k is the average branching factor for the board. Let’s look at how rapidly this grows! For a board that is 5x5 the tree will be 25 levels deep, or N = 24 counting the first level as level 0. The average branching factor is k = 3 . 8 k = 3.8 k = 3 . 8 So the number of nodes in the search tree is 3 . 8 2 5 − 1 3.8^{25}-1 3 . 8 ​ 2 5 ​ ​ − 1 or 3 . 1 2 × 1 0 1 4 3.12 \times 10^{14} 3 . 1 2 × 1 0 ​ 1 4 ​ ​ . For a 6x6 board, k = 4 . 4 k = 4.4 k = 4 . 4 , there are 1 . 5 × 1 0 2 3 1.5 \times 10^{23} 1 . 5 × 1 0 ​ 2 3 ​ ​ nodes, and for a regular 8x8 chess board, k = 5 . 2 5 k = 5.25 k = 5 . 2 5 , there are 1 . 3 × 1 0 4 6 1.3 \times 10^{46} 1 . 3 × 1 0 ​ 4 6 ​ ​ . Of course, since there are multiple solutions to the problem we won’t have to explore every single node, but the fractional part of the nodes we do have to explore is just a constant multiplier which does not change the exponential nature of the problem. We will leave it as an exercise for you to see if you can express k k k as a function of the board size.

Luckily there is a way to speed up the eight-by-eight case so that it runs in under one second. In the code sample below we show the code that speeds up the traverse . This function, called warnsdorffs_heuristic when passed as the heuristic function to find_solution_for above will cause the next_vertices to be sorted prioritizing those who which have the fewest subsequent legal moves.

This may seem counterintutitive; why not select the node that has the most available moves? The problem with using the vertex with the most available moves as your next vertex on the path is that it tends to have the knight visit the middle squares early on in the tour. When this happens it is easy for the knight to get stranded on one side of the board where it cannot reach unvisited squares on the other side of the board. On the other hand, visiting the squares with the fewest available moves first pushes the knight to visit the squares around the edges of the board first. This ensures that the knight will visit the hard-to- reach corners early and can use the middle squares to hop across the board only when necessary. Utilizing this kind of knowledge to speed up an algorithm is called a heuristic. Humans use heuristics every day to help make decisions, heuristic searches are often used in the field of artificial intelligence. This particular heuristic is called Warnsdorff’s heuristic, named after H. C. Warnsdorff who published his idea in 1823, becoming the first person to describe a procedure to complete the knight’s tour.

For fun, here is a very large ( 1 3 0 × 1 3 0 130 \times 130 1 3 0 × 1 3 0 ) open knight’s tour created using Warnsdorff’s heuristic:

• The Big Picture
• Big O Notation
• An Anagram Detection Example
• Performance of Python Types
• Introduction to Stacks
• A Stack Implementation
• Balanced Parentheses
• Converting Number Bases
• Infix, Prefix and Postfix Expressions
• Introduction to Queues
• A Queue Implementation
• Simulating Hot Potato
• Introduction to Deques
• A Deque Implementation
• Palindrome Checker
• Introduction to Lists
• Implementing an Unordered List
• Implementing an Ordered List
• Introduction to Recursion
• Calculating the Sum of a List of Numbers
• The Three Laws of Recursion
• Converting an Integer to Any Base
• Tower of Hanoi
• Dynamic Programming
• The Sequential Search
• The Binary Search
• Introduction to Trees
• Representing a Tree
• Parse Trees
• Tree Traversals
• Priority Queues with Binary Heaps
• Binary Search Trees
• Introduction to Graphs
• Representing a Graph
• Word Ladders
• General Depth First Search
• Topological Sorting
• Shortest Path with Dijkstra’s Algorithm
• Strongly Connected Components
• Prim’s Spanning Tree Algorithm

Euler and the Knight's Tour

It is the program of choice for anyone who loves the game and wants to know more about it. Start your personal success story with ChessBase and enjoy the game even more.

ONLINE SHOP

The flexible taimanov sicilian + a complete guide for black against the anti-sicilian.

Looking for a realistic way to play for a win with Black against 1.e4 without taking unnecessary risks? The Taimanov Sicilian is a reliable system, and hence one of the best options out there!

€69.90

Master Class Vol.9: Paul Morphy

Learn about one of the greatest geniuses in the history of chess! Paul Morphy's career (1837-1884) lasted only a few years and yet he managed to defeat the best chess players of his time.

User   Password  

Not registered yet? Register

Fritz 19 & Opening Encyclopaedia 2024

The best combination for opening training: The big ChessBase opening encyclopaedia with thousands of opening articles plus Fritz19 at a special price!

€199.90

The flexible Taimanov Sicilian

€49.90

A Complete Guide for Black against the Anti-Sicilian

Have you always wanted to play the Sicilian as Black, but been discouraged by the abundance of options for White? Here is the solution to becoming a lifelong successful Sicilian player!

€39.90

French Defence Powerbook 2024

The main part of the material on which the French Powerbook 2024 is based comes from the playchess.com engine room: 730,000 games. An impressive number to which 90,000 games from correspondence chess and the Mega were added.

French Defence Powerbase 2024

The French Defence Powerbase 2024 is a database and contains 10.846 games from the Mega 2024 and the Correspondence Database 2024, 707 of which are annotated.

ChessBase Magazine Extra 220

Videos by Felix Blohberger: Repertoire idea against the Reti Opening and Mihail Marin: Nepo’s Petroff. "Lucky bag" with 36 analyses by Bogdan Deac, Shreyas Royal, Samuel Shankland, Vaibhav Suri and many more. Update Service with over 55,000 new games!

€14.90

How to Avoid Mistakes and Boost Your Winning Rate

Doesn’t every chess game get decided by mistakes? Absolutely. But most players never truly comprehend that they are making the same kind of mistakes over and over again.

€36.90

Pop-up for detailed settings

We use cookies and comparable technologies to provide certain functions, to improve the user experience and to offer interest-oriented content. Depending on their intended use, cookies may be used in addition to technically required cookies, analysis cookies and marketing cookies. You can decide which cookies to use by selecting the appropriate options below. Please note that your selection may affect the functionality of the service. Further information can be found in our privacy policy .

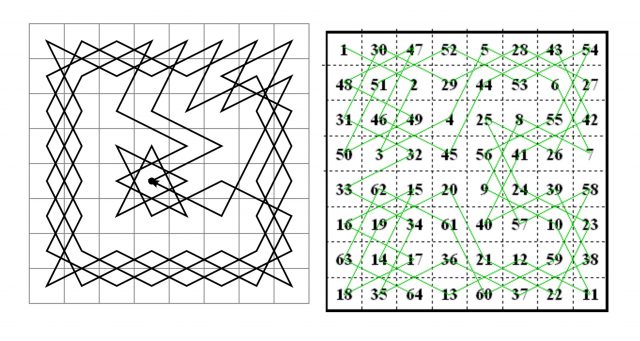
Knight's Tour (10x10)

Click on a square to start the tour.

Speed: slow normal fast

Some Closed Knight's Tours

A cyclic knight's tour is a sequence of knight's moves that visit every square of an n x n chessboard, returning to the first square. These are some images from Ian Parberry 's research on cyclic knight's tours in the 1990s. See these papers for more information. Some of the tours are generated by a random walk, one is generated by a neural network, some are generated by a divide-and-conquer algorithm that gives the tours a tiled look. Some are symmetric under rotations.

6x6, Random

The following small knight's tour was used as part of the base of the recursion in a divide-and-conquer algorithm described in Ian Parberry , "An Efficient Algorithm for the Knight's Tour Problem", Discrete Applied Mathematics , Vol. 73, pp. 251-260, 1997. [ pdf ].

8x8, Random

10x10, random.

The following small knight's tour was used as part of the base of the recursion in a divide-and-conquer algorithm described in Ian Parberry , "An Efficient Algorithm for the Knight's Tour Problem", Discrete Applied Mathematics , Vol. 73, pp. 251-260, 1997. [ pdf ]. You may have noticed by now that all of the closed knight's tours you have seen so far (6x6, 8x8, and 10x10) have even sides. That's because there can be no knight's tours on an odd-sided board (to see this, consider the fact that on a real chessboard, the squares visited in a knight's tour must alternate between black and white).

10x10, Invariant Under 90° Rotation

Closed knight's that are invariant under a 90° rotation exist on nxn boards for all even n at least 6 that is not divisible by 4 (Dejter, 1983). This tour is from Ian Parberry , "An Efficient Algorithm for the Knight's Tour Problem", Discrete Applied Mathematics , Vol. 73, pp. 251-260, 1997. [ pdf ].

12x12, Invariant Under 180° Rotation

Closed knight's that are invariant under a 180° rotation exist on nxn boards for all even n at least 10. This tour is from Ian Parberry , "An Efficient Algorithm for the Knight's Tour Problem", Discrete Applied Mathematics , Vol. 73, pp. 251-260, 1997. [ pdf ], as are the following 14x14, 16x16, 18x18, and 20x20 knight's tours.

14x14, Invariant Under 90° Rotation

18x18, invariant under 90° rotation, 20x20, invariant under 180° rotation, 26x26, found by a neural network.

The following was the largest closed knight's tour I could generate at the time using the Hopfield network of Takefuji and Lee. More details appear in Ian Parberry , "Scalability of a Neural Network for the Knight's Tour Problem", Neurocomputing , Vol. 12, pp. 19-34, 1996. [ pdf ]

The following was generated by a divide-and-conquer algorithm described in "An Efficient Algorithm for the Knight's Tour Problem", Discrete Applied Mathematics , Vol. 73, pp. 251-260, 1997. [ pdf ].

60x60, Random Walk with Warnsdorf's Heuristic

The following was generated by a random walk algorithm due to Euler in 1795 modifed with a heuristic due to Warnsdorf in 1823. It appears in Ian Parberry , "Scalability of a Neural Network for the Knight's Tour Problem", Neurocomputing , Vol. 12, pp. 19-34, 1996. [ pdf ]

Created April 23, 2010. Last updated November 18, 2022.

• Practice Backtracking
• Interview Problems on Backtracking
• MCQs on Backtracking
• Tutorial on Backtracking
• Backtracking vs Recursion
• Backtracking vs Branch & Bound
• Print Permutations
• Subset Sum Problem
• N-Queen Problem
• Knight's Tour
• Sudoku Solver
• Rat in Maze
• Hamiltonian Cycle
• Graph Coloring

The Knight’s tour problem

Backtracking is an algorithmic paradigm that tries different solutions until finds a solution that “works”. Problems that are typically solved using the backtracking technique have the following property in common. These problems can only be solved by trying every possible configuration and each configuration is tried only once. A Naive solution for these problems is to try all configurations and output a configuration that follows given problem constraints. Backtracking works incrementally and is an optimization over the Naive solution where all possible configurations are generated and tried. For example, consider the following Knight’s Tour problem. 

Problem Statement: Given a N*N board with the Knight placed on the first block of an empty board. Moving according to the rules of chess knight must visit each square exactly once. Print the order of each cell in which they are visited.

The path followed by Knight to cover all the cells Following is a chessboard with 8 x 8 cells. Numbers in cells indicate the move number of Knight. 

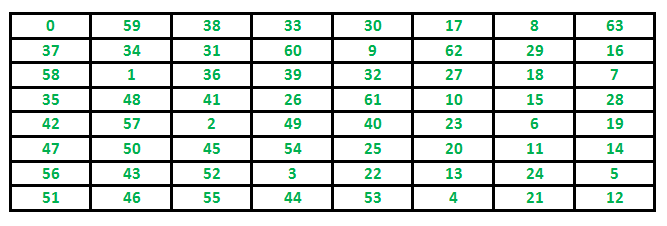
Let us first discuss the Naive algorithm for this problem and then the Backtracking algorithm.

Naive Algorithm for Knight’s tour   The Naive Algorithm is to generate all tours one by one and check if the generated tour satisfies the constraints. 

Backtracking works in an incremental way to attack problems. Typically, we start from an empty solution vector and one by one add items (Meaning of item varies from problem to problem. In the context of Knight’s tour problem, an item is a Knight’s move). When we add an item, we check if adding the current item violates the problem constraint, if it does then we remove the item and try other alternatives. If none of the alternatives works out then we go to the previous stage and remove the item added in the previous stage. If we reach the initial stage back then we say that no solution exists. If adding an item doesn’t violate constraints then we recursively add items one by one. If the solution vector becomes complete then we print the solution.

Backtracking Algorithm for Knight’s tour  

Following is the Backtracking algorithm for Knight’s tour problem. 

Following are implementations for Knight’s tour problem. It prints one of the possible solutions in 2D matrix form. Basically, the output is a 2D 8*8 matrix with numbers from 0 to 63 and these numbers show steps made by Knight.   

Time Complexity :  There are N 2 Cells and for each, we have a maximum of 8 possible moves to choose from, so the worst running time is O(8 N^2 ).

Auxiliary Space: O(N 2 )

Important Note: No order of the xMove, yMove is wrong, but they will affect the running time of the algorithm drastically. For example, think of the case where the 8th choice of the move is the correct one, and before that our code ran 7 different wrong paths. It’s always a good idea a have a heuristic than to try backtracking randomly. Like, in this case, we know the next step would probably be in the south or east direction, then checking the paths which lead their first is a better strategy.

Note that Backtracking is not the best solution for the Knight’s tour problem. See the below article for other better solutions. The purpose of this post is to explain Backtracking with an example.  Warnsdorff’s algorithm for Knight’s tour problem

References:  http://see.stanford.edu/materials/icspacs106b/H19-RecBacktrackExamples.pdf   http://www.cis.upenn.edu/~matuszek/cit594-2009/Lectures/35-backtracking.ppt   http://mathworld.wolfram.com/KnightsTour.html   http://en.wikipedia.org/wiki/Knight%27s_tour    

Please Login to comment...

Similar reads.

• Backtracking
• Mathematical
• chessboard-problems

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Knight's Tour Challenge

How to play.

This "game" is basically an implementation of Knight's Tour problem.

You have to produce the longest possible sequence of moves of a chess knight, while visiting squares on the board only once. This sequence is called "tour". If your tour visits every square, then you have achieved a full tour. If you have achieved a full tour and from your last position you could move to your initial square, then you have achieved a closed full tour.

Currently occupied square is highlighted in pale blue, while possible moves are shown with pale green. Click on the currently occupied square to undo.

A Python solution for a classic chess puzzle

Knight's tour.

© Lead Image © Dima Sobko, 123RF.com

If you're looking for a head start on solving the classic Knight's Tour chess challenge, try this homegrown Python script.

A chess knight can travel around a chessboard using the knight's move and visit every square once, and only once. This is known as the Knight's Tour. The Knight's Tour is usually played with numbered counters on a conventional chessboard ( Figure 1 ), but you can play it on any rectangular board with five or more rows and columns.

The Knight's Tour is an example of a classic mathematical problem that lends itself to easy and creative expression through computer programming. I created a Python program to help users practice solving the Knight's Tour. The Knight's Tour program is a good example of the simple yet powerful applications you can build with the Pygame Python library for computer gamers.

Solving the Knight's Tour

At first, solving the Knight's Tour seems to be a daunting challenge, but quite a few strategies exist that will help you solve the puzzle [1] . I'll consider just two of them. The first strategy is usually known as the Diamonds and Squares method, and it's a simple party trick that anyone can learn in minutes.

Solving the Knight's Tour using the Diamonds and Squares technique doesn't require any mathematical talent or much logical skill; it merely requires the player to recognize two simple geometric shapes in the patterns of knight's moves. This approach can produce a relatively small number of apparently unique tours from every starting square, but the symmetry of the chessboard means that many of these solutions are transformations of other tours by rotation, reflection, or inversion, and this simple technique can only produce 46 truly unique Knight's Tours on a chessboard. Most of the Knight's Tour solution videos you watch on YouTube and elsewhere demonstrate the Diamonds and Squares method.

The second approach is known as Warnsdorff's rule. This strategy takes a bit more effort to master. On an 8x8 chessboard, it can produce thousands of different Knight's Tours from any starting square, but, again, the symmetry of the chessboard means that not all of these solutions are truly unique and many of them are transformations of other Warnsdorff's rule tours. As you'll see in a moment, Warnsdorff's rule can sometimes lead to an impasse, but it still produces far more solutions than the Diamonds and Squares method.

If you want to impress your friends by showing them how to solve the Knight's Tour, then using Warnsdorff's rule will not expose you as a chess puzzle pretender, but using the simple Diamonds and Squares technique might put your reputation as a chess puzzle genius in jeopardy.

Diamonds and Squares

The Diamonds and Squares technique was first described by C. R. R. von Schinnern in 1826 [1] . It only works on boards that have at least 8x8 squares. Larger boards must have a number of rows and columns that are a multiple of four (i.e., 12x12, 8x16, and so on). Unlike Warnsdorff's rule, the Diamonds and Squares technique cannot be used to solve the Knight's Tour on a 6x6 or a 10x10 board.

To employ the Diamonds and Squares strategy on a conventional 8x8 chessboard, you need to divide the chessboard into four quadrants and understand how four knights can be placed on a quadrant in four distinct patterns. The first of these patterns is described as a right-hand (RH) diamond ( Figure 2a ). The second is a left-hand (LH) diamond ( Figure 2b ), the third is a RH square ( Figure 2c ), and the last one is a LH square ( Figure 2d ). When these four shapes are joined together on one quadrant of the chessboard, all 16 squares in that quadrant will have a knight on them.

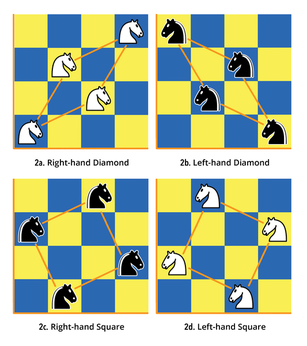
In order to use the diamond and square shapes to solve the Knight's Tour, you need to know whether the first knight placed on the board is on a diamond (either RH or LH) or on a square (either RH or LH). For example, a knight at b3 is on a RH diamond ( Figure 3a ), one at c4 is on a RH square ( Figure 3b ), a knight at d1 is on a LH diamond ( Figure 3c ), and one at d3 is on a LH square ( Figure 3d ).

If you place the first knight on, for example, b3, then you can complete a four-knight partial tour in the lower left-hand quadrant with four knights on a RH diamond shape ( Figure 3a ). You then move onto an adjacent quadrant and use a RH diamond shape to complete another four-knight partial tour on that quadrant. Then you can move on to a third quadrant and then the fourth so that all four quadrants have a four-knight, RH diamond-shaped partial tour on them, and there are 16 knights on the board ( Figure 3a ). After completing the RH diamond-shaped partial tour, you move on to a square-shaped partial tour, in this example, a RH square-shaped partial tour starting at c4 and ending at d6 ( Figure 3b ). Then you can complete a LH diamond-shaped partial tour starting at e8 and ending at b6 ( Figure 3c ) and finally a LH square-shaped partial tour starting at d7 and ending at g5 to complete the Knight's Tour ( Figure 3d ).

The Knight's Tour can always be solved by combining two, 16-knight, diamond-shaped, LH and RH partial tours and two, 16-knight, square-shaped, LH and RH partial tours in the order diamond-square-diamond-square or square-diamond-square-diamond. You will need to make sure that the fourth knight placed in each quadrant leads to an empty square on an adjacent quadrant. With a bit of practice, it's quite easy to solve the Knight's Tour from any starting square using this method.

You can find variations of the Diamonds and Squares technique that will allow you to choose the starting and ending square, but be warned, nearly everyone who knows about the Knight's Tour knows about the Diamonds and Squares method, and you can only impress naive chess puzzlers by demonstrating this technique.

Warnsdorff's Rule

The second strategy is known as Warnsdorff's rule [1, 2] and it is named after H. C. von Warnsdorff, who first described it in 1823. Warnsdorff's rule is a heuristic or rule-of-thumb method for finding a Knight's Tour from any starting square on any sized board with at least 5x5 squares. I'll look at it on a conventional chessboard.

Warnsdorff's rule is summarized as follows:

1. With each move, you have to look ahead to see which of the possible next moves has the least number of exits that can be taken using the knight's move ( Figure 4 ). An exit is a legal move to a square that the knight hasn't inhabited yet.

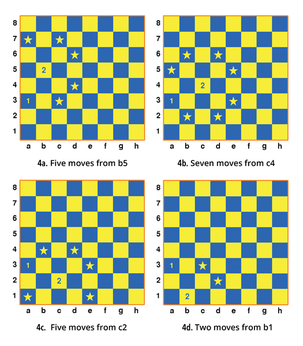
2. The square with the least number of valid exits is chosen for the next move.

3. If there is a tie between two or more squares, the next square is chosen at random from all the squares with the least number of exits.

Unfortunately, if a Monte Carlo test [3] is done when Warnsdorff's rule is applied to a conventional chessboard, about three percent of the attempts to find a complete tour will lead to an impasse. If you want to find a Knight's Tour every time using Warnsdorff's rule, you need to modify the original rule to overcome any impasse that might occur. Do this by replacing the random choice of a tiebreaker with a systematic choice.

The easiest variant of Warnsdorff's rule to implement in a computer program requires very little coding. It modifies the third element of Warnsdorff's rule so that, if there is a tie for the next move between two or more squares, the next square is chosen systematically – any systematic way of choosing the tiebreaker will do as long as it prioritizes the way in which the tied moves are selected to break the tie. If breaking a tie systematically leads to an impasse, the calculation can just start again using a different way of making a systematic choice. This is quite a good option for a computer program, because a computer can find a complete tour using an alternative way of choosing a tiebreaker in milliseconds. The program overcomes any impasse that might occur using this simple plan – if the way you're choosing a tiebreaker doesn't work, then stop using it, start again, and choose your tiebreaker in a different way.

Another variant of Warnsdorff's rule is better if you're trying to find a way out of an impasse by hand, because it usually involves less work than starting again. If systematic tie breaking leads to an impasse, you can backtrack to the last tiebreaker and take the second-priority move. If that doesn't work, you can backtrack again and choose the third-priority move, and so on until all the tiebreakers have been tried. If that doesn't overcome the impasse, backtrack to the last-but-one tiebreaker, select the second priority tiebreaker, and keep doing this until the impasse is overcome. The computer program will enable you to backtrack in this way if you're using Warnsdorff's rule (or any other strategy) to solve the puzzle by hand and you get stuck in an impasse. The program doesn't use backtracking when it's finding a solution for you, but if you'd like to see how a program can use backtracking to find a way out of an impasse, there's a backtracking algorithm used in a Knight's Tour program I wrote when I first became interested in chess puzzles many years ago. This program was published in The Century/Acorn User Book of Computer Puzzles [4] .

Any systematic way of choosing can be used as a tiebreaker for either of the alternative versions of Warnsdorff's rule described above, but remember, it must be a systematic choice rather than a random one. There are eight factorial ( 8! = 40320 ) ways in which you can make a systematic choice, but two of the easiest ones to remember when finding a Knight's Tour by hand are to select the tiebreaker in either a clockwise or counterclockwise direction starting at the 12 o'clock position (i.e., start looking from the top of the board and work your way around the tied moves to the right or to the left).

A very handy shortcut version of Warnsdorff's rule can be used to place the first 30 or so knights on the board. This technique works because, in the first half of solving the puzzle, selecting the square with the least number of exits is usually the same as moving the knight as far away from the center of the board as possible – but beware, this shortcut will occasionally disappoint you.

The shortcut requires you to stay as close to the edge of the board as possible and to prioritize the corner squares and their adjacent perimeter squares. This will usually result in two circuits of the board's perimeter during the first half of the tour, after which it's better to stop using the shortcut and start calculating the best way around the empty squares on the board using systematic tie breaking. An insight into what's needed to solve the puzzle is also very useful during the second half of the tour, and you will develop the necessary insight with practice. The fewer knights that are placed on the board using this shortcut, the better it works. The shortcut becomes less reliable as more knights are placed on the board, and the chance that it will let you down increases noticeably when there are more than half of the knights on the board. The Knight's Tour shown in Figure 5 was found using this shortcut combined with backtracking and insight. With practice, it takes only a couple of minutes to find a complete Warnsdorff's tour by hand.

1 2 Next »

Buy this article as PDF

Buy linux magazine.

US / Canada

UK / Australia

Related content

In the absence of an IBM supercomputer at his data center in Germany's Lower Rhine region, Charly has to make do with a Linux desktop, Stockfish, and chs in order to follow in the footsteps of chess grandmaster Garry Kasparov.

Some regard Sudoku as the 21st

century Rubik’s Cube. We’ll

show you how to get started

with Sudoku in Linux.

Shredder 9 promises world championship chess on your home computer. We took a look at the new Linux version of the famous Shredder chess tool.

In part 3 of our gamers recommandations we present more strategy games, puzzles, card games, language skill training and more. To be continued.

Seven-city tour presents strategies and best practices for building open clouds.

Subscribe to our Linux Newsletters Find Linux and Open Source Jobs Subscribe to our ADMIN Newsletters

Support our work.

Linux Magazine content is made possible with support from readers like you. Please consider contributing when you’ve found an article to be beneficial.

Plasma Desktop 6.1.4 Release Includes Improvements and Bug Fixes

The latest release from the KDE team improves the KWin window and composite managers and plenty of fixes.

Manjaro Team Tests Immutable Version of its Arch-Based Distribution

If you're a fan of immutable operating systems, you'll be thrilled to know that the Manjaro team is working on an immutable spin that is now available for testing.

Nitrux 3.6.0 ("ie") Available for Download and Install

The latest version of the systemd-free Linux distribution, Nitrux, has been released for general usage and includes the beta of the upcoming NVIDIA 560 graphics driver.

Vanilla OS 2 Available for Download

The latest iteration of Vanilla OS (Orchid) has been released and uses a hybrid Debian base.

Debian-Based eLxr Distribution Announced for Edge Deployments

Open source eLxr offers a seamless operating environment for edge-to-cloud deployments.

NVIDIA Released Driver for Upcoming NVIDIA 560 GPU for Linux

Not only has NVIDIA released the driver for its upcoming CPU series, it's the first release that defaults to using open-source GPU kernel modules.

OpenMandriva Lx 24.07 Released

If you’re into rolling release Linux distributions, OpenMandriva ROME has a new snapshot with a new kernel.

Kernel 6.10 Available for General Usage

Linus Torvalds has released the 6.10 kernel and it includes significant performance increases for Intel Core hybrid systems and more.

TUXEDO Computers Releases InfinityBook Pro 14 Gen9 Laptop

Sporting either AMD or Intel CPUs, the TUXEDO InfinityBook Pro 14 is an extremely compact, lightweight, sturdy powerhouse.

Google Extends Support for Linux Kernels Used for Android

Because the LTS Linux kernel releases are so important to Android, Google has decided to extend the support period beyond that offered by the kernel development team.

Uncrossed Knight's Tour

We conclude our exploration of the ancient challenge of knight’s tours with the uncrossed tour or non-intersecting tour.

Your task is to find the longest possible path of a knight (using standard chess knight moves) in such a way that the path does not intersect itself. 

A further distinction can be made between a “closed path,” which ends on the same field as where it begins, and an “open path,” which ends on a different field from where it begins.

The first recording of this variant on knight’s tours was in the Journal of Recreational Mathematic of July 1968 by L. D. Yarbrough. What I love about this challenge is that Yarbrough only found an open uncrossed path of 16 on a 6x6 tour but another mathematician, Martin Gardner in his 1979 book, “Mathematical Circus,” explains that the 6x6 tour found by Yarbrough can be improved from 16 to 17 jumps.

On the worksheets I provided to the children, they were told the maximum solutions for the open and closed tours on boards of 3x3, 4x4, 5x5, 6x6, 8x8, and 10x10. For example, on the traditional chess board of 8x8, the maximum uncrossed knight’s tour is 35 on an open tour and 32 on a closed tour. For years, I have only been able to accomplish a solution of 28 on a closed tour so I challenged the children to beat my solution of 28 on an 8x8 closed tour. They may even get the help of their parents (no internet). If they do exceed my 28, they will get their picture on a mathlete dollar.

The key strategy is to explore the board in a way that hits as many squares as possible. Try not to miss an opportunity to reach areas of the board that can increase the number of moves. I have found that creating acute angles vs. obtuse angles will increase the number of moves.

I also suggested to the children that for each closed tour that they accomplish on any board, they should color in the polygon. A polygon is named by its number of sides. For example, on a 5x5 board, the maximum uncrossed closed knight’s tour is 8 moves and forms an octagon.

• Lesson Archive

Acadiana Kickoff Tour 2024: Lafayette Christian Knights

Lafayette Christian Knights 2023 Record: 11-3 District: 6-2A Head Coach: Zach Lochard Notes: Knights welcome Lochard to lead the team, after spending two seasons at Breaux Bridge

Lafayette Christian has been to seven straight championship appearances, but their last title came in 2020 to cap off a "4 for 4" run.

This year, they're "new look Knights" with the addition of a new head coach.

After spending two seasons at Breaux Bridge, Zach Lochard made the switch to LCA, a program that he says is his dream job.

“We all knew what we was getting into, we needed a new head coach, a new staff and he brought new people in and looking back, nothing is really different", says senior running back Jalen Noel. "We’re still doing the work we need to do, we’re building as a family and a brotherhood.”

“This is a place I want to be for 35 years until I retire. I’m a faith, family, football kind of guy. It’s a great community and just a great place for me and my family", Lochard claims.

LCA will welcome new faces but according to Lochard, returns nearly everyone on offense.

But the question is, who'll lead this team following the record-breaking success of former Knight, Ju'Juan Johnson?

LCA says no need to fear, Walker is here.

“Braylon Walker is the dude. Anybody across the nation, once they got to knew him, would want him on their team. He’s a 4.0 student, he is a student of the game, he brings so much energy and excitement. He has so much passion and attention to detail. He’s got a rocket arm and lightening for speed."

"He’s a great guy and a great leader. He leads by example", says senior athlete, Calvin Parker. "He can also be a vocal leader at times when he needs. He’s going to do the right thing and we trust him that he’s going to do the right thing."

The motto for the Knights is simple — that's to finish the task at hand.

------------------------------------------------------------ Stay in touch with us anytime, anywhere.

To reach the newsroom or report a typo/correction, click HERE .

Sign up for newsletters emailed to your inbox. Select from these options: Breaking News, Evening News Headlines, Latest COVID-19 Headlines, Morning News Headlines, Special Offers

Follow us on Twitter

Like us on Facebook

Follow us on Instagram

Subscribe to our Youtube channel

Sign up for the Headlines Newsletter and receive up to date information.

Now signed up to receive the headlines newsletter..

Related Guides:

Novosibirsk

Novosibirsk tourist information and tourism, (novosibirsk, siberia, russia), novosibirsk tourist information and tourism: top sights, more novosibirsk information / fast facts and orientation.

• Country: Russia (Russian Federation)
• Location: Novosibirsk Oblast region / Southern Siberia
• Status: city / capital of Siberia
• Area: approximately 193 square miles / 500 square kilometres
• Population: approximately 1.5 million
• Language: Russian
• Currency: Russian Ruble (RUR)
• Time zone: UTC / GMT +3
• Country dialing code: +7
• Telephone area code: 383
• Average daily Novosibirsk January temperature: -14°C / 7°F
• Average daily Novosibirsk July temperature: 25°C / 77°F

© Copyright TravelSmart Ltd

I'm looking for:

Hotel Search

• Travel Guide
• Information and Tourism
• Maps and Orientation
• Transport and Car Rental
• History Facts
• Weather and Climate
• Accommodation
• Hotels and Accommodation
• Popular Attractions
• Tourist Attractions
• Museums and Art Galleries
• Attractions Nearby
• Things to Do
• Events and Festivals
• Restaurants and Dining
• Your Reviews of Novosibirsk
• Russia World Guide
• Guide Disclaimer
• Privacy Policy / Disclaimer

Charlotte Knights Roster & Staff

Category : People of Novosibirsk Oblast

Subcategories.

This category has the following 11 subcategories, out of 11 total.

• Heads of Novosibirsk Oblast ‎ (2 C, 1 F)
• People in Novosibirsk Oblast ‎ (3 C, 9 F)
• Deaths in Novosibirsk Oblast ‎ (2 C)
• Georgy Baydukov ‎ (1 C, 25 F)
• Births in Novosibirsk Oblast ‎ (2 C)
• Yuri Ilyin ‎ (6 F)
• People of Koltsovo (Novosibirsk Oblast) ‎ (1 C, 1 F)
• People of Novosibirsk ‎ (62 C, 55 F)
• Origa ‎ (1 F)
• People of Berdsk ‎ (4 C, 1 F)
• Ivan Starikov ‎ (16 F)

Media in category "People of Novosibirsk Oblast"

The following 2 files are in this category, out of 2 total.

• People of Russia by region
• Novosibirsk Oblast
• Uses of Wikidata Infobox
• Uses of Wikidata Infobox with subinfoboxes
• Uses of Wikidata Infobox with maps
• Pages with coordinates

Navigation menu

Jordan Knight and NKOTB plan to impress hometown crowd with ‘Magic’ Mansfield show

‘there’s always an extra level of energy when we go to the boston area,’ knight said ahead of new kids on the block’s return to the xfinity center this weekend.

It’s been a sizzling summer for Jordan Knight and his fellow New Kids on the Block bandmates as the group has been traveling North America in support of their “Magic Summer 2024 Tour,” a new spin on their legendary 1990s tour of the same name.

The summer concerts have definitely brought the heat, with a July show in Phoenix seeing temperatures peak at 115 degrees, which was a bit “scary,” according to Knight, but that couldn’t stop the boy band from hangin’ tough .

“The heat’s been a factor, but it’s just fun to be outside,” Knight told the Globe in a recent phone interview, noting how their last full tour of outdoor venues was in 2009. “It’s fun to do something different.”

“The tour has been like any other New Kids tour; it’s just a lot of fun,” he added. “A lot of love, a lot of laughs, a lot of excitement.”

Advertisement

When the New Kids embarked on their first magic summer in 1990, the group stopped at the old Foxboro Stadium, but this time around the tour will take over the Xfinity Center in Mansfield on Saturday, accompanied by special guests Paula Abdul and DJ Jazzy Jeff.

The band has a lot of history with the venue, first playing it in 1988 when it was called Great Woods. Earlier this year, Knight’s bandmate Joey McIntyre praised the amphitheater for providing “an energy to those summer nights underneath the stars.” Knight echoed those sentiments, calling it one of the area’s top places to play alongside spots like TD Garden and Fenway Park.

“Those are all just great venues,” Knight said.

Aside from having nearby friends and family come out to the show, playing in Massachusetts comes with other perks for Knight: He can sleep in his own bed. The 54-year-old singer — who grew up in Dorchester with his brother and fellow boy bander Jonathan — lives in Milton, where he co-owns the restaurant Novara , along with two other spots in town.

“Every winter I’m like, ‘Why the hell do I live here?’ But I’ve never left,” Knight said. “I still live in Milton with my wife. My older son’s moved out. My younger son’s still with us. They went to schools in the area.”

His brother lives in Essex on a farm and, when there isn’t a New Kids tour, can be seen hosting the HGTV series “Farmhouse Fixer” with designer Kristina Crestin. Jordan Knight said it’s always a joy to visit his sibling, whether for fun or to help out on the home makeover show.

“We go up there all the time and celebrate things, birthdays, holidays,” Knight said.

As for the upcoming concert in Mansfield, the New Kids star wouldn’t divulge any secrets, but did tease a few surprises in store for the hometown crowd.

“I will just say, we always cook up surprises,” Knight said. “We won’t let people down.”

Since so many family, friends, and local fans will be in attendance, expect Knight and the rest of the New Kids to bring the right stuff on Saturday night.

“Pardon the pun, but we’re still kids inside. We want to impress,” Knight said. “There’s always an extra level of energy when we go to the Boston area.”

NEW KIDS ON THE BLOCK: MAGIC SUMMER 2024 TOUR

With Paula Abdul and DJ Jazzy Jeff

At Xfinity Center, Mansfield. Saturday at 7 p.m. livenation.com

Matt Juul can be reached at [email protected] .