causal nexus time travel

Your complimentary articles

You’ve read one of your four complimentary articles for this month.

You can read four articles free per month. To have complete access to the thousands of philosophy articles on this site, please

Tallis in Wonderland

The myth of time travel, raymond tallis time travels merely by the power of thought..

There are many reasons why we should not waste our time speculating about the possibility of time travel. Some are obvious; others are less so. The most obvious problems arise from the contradictions that result when the traveller goes backwards in time – which I will focus on here – although they also apply to travel into the future.

The best-known objection goes as follows. Supposing I return to the day my parents first met, 6th June 1933. I distract one of them and they do not see each other; their relationship never happens, and I am not born. By interfering with the past, I have removed the most essential condition for my journey to the past – namely, that I should exist. More generally, if I really were able to return to an earlier date than the present, I could be in a position to disturb any of the conditions that resulted in my being able to engage in time travel. More generally still, any action that I take at my past destination date – not just events that have a direct and traceable influence on my personal history – will generate contradictions: it will have an impact on the subsequent history of the universe, and hence on the contents of the day from which I set out, for every event has a direct or indirect influence on every other event.

My departure date – let us say 5th September 2009 – would therefore have two versions: the one that I set out from, and the one that existed after I have interfered with one of its predecessors. How will these two versions of 05/09/09 relate to one another? Do they exist side by side, simultaneously as parts of parallel universes? Seemingly not, as they do not come into being at the same time – at least if time travel takes time (of which more presently). The version of the day I set out from will from my perspective precede the version of the day that will result from my arriving at its antecedents and disturbing the course of subsequent events. The same considerations will apply to the destination day 6th June 1933. It, too, will have two versions. Before I set out, Raymond Tallis will be present in it only as a future possibility not yet born; after I have landed, I will be present in it as a fully-grown actuality. In this case, the first version will be in place 76 years before the second version. And yet in the flow of history they will both lay claim to being the same day. This is, of course, unacceptable: the least we might expect of a day is that it should be simultaneous with, and identical to, itself!

Though we cannot get round the difficulty of having two occurrences of the same day, could we at least make sure that both occurrences would have the same contents? In order to arrange this, I would have to be prevented from doing anything at all when I arrive at 6th June 1933: it would have to be undisturbed, in order that its successors, including 5th September 2009, should be unaltered. Unfortunately this is an impossible requirement. Even if I were prevented from acting, and were weightless and held my breath, I would still have to interact with my surroundings for them to be present to me, for me to have arrived . For example, seeing those surroundings interferes with the light. In short, I could not be present at a destination day without affecting it.

This difficulty shows an important requirement at the heart of the notion of time travel: that the traveller should be causally insulated from the rest of the universe. In the traditional model, the traveller enters a machine and she and the machine leave the present for the past. To do this, the woman-machine complex has to break with the causal nexus it is embedded in before departure. This follows from the fact that it is going backwards in time, while the rest of the universe is moving forward in time. The only way to avoid this rupture would be for everything else to come along for the ride. If, however, the entire universe were wound backwards, there would be no experience, or indeed reality, of travelling away from the present into the past: there would be no clock or consciousness unaffected by the backward movement, able to register my journey. In short, time travel requires one small part of the universe – human plus machine – to break ranks with the rest.

There are therefore causal difficulties in both the departure lounge and the arrival hall. Here is another difficulty: how could we travel in time without travelling in space? ‘The same place’ in 1933 would not be at the same place in 2009. The planet, the solar system and even the galaxy are in different places relative to the universe at large. Moreover, given that time travel cannot be without causal imprint, this also means that even the spatio-temporal co-ordinates of the place would be altered.

That’s not the end of the barriers to time travel that should make us highly sceptical even of its logical possibility, never mind its practicability. How, for example, could the traveller alight at a particular target date? To do so, she would need to specify how far in time she is to travel, and hence the speed and duration of the journey. These parameters – speed and duration – are problematic, to say the least. The notion of the speed of travel through time, and of the duration of the journey, would make sense only with respect to a hypertime , a second-order time whose passage would time the passage of time as she makes a passage through time. This is an impossible conception. And if the journey did take time, the destination would recede further into the past even as the traveller advanced towards it. The only way to ensure arrival would be to time-travel backwards much faster than time unfolds. And even if we could get over these little difficulties, it would be interesting to know by what means the traveller would successfully alight on a particular target date. (The notion of travel as opposed to mere movement assumes that the journey is under our control.) How could the machine be brought to a halt at the chosen destination? Given that the time traveller has to shake off the causal bonds at her setting-off point, and is beyond the grasp of causation in all intermediate locations, what causal brakes could be applied?

Unrelative Dimensions

These and many other problems with time travel show that it is an entirely incoherent idea. It hardly deserves a shrug. How then has it managed to capture so much attention? To understand why the possibility of time travel is taken seriously, we need to remind ourselves of the grip the notion of time as a quasi-spatial dimension has on our thinking. If time truly is comparable to space, then moving backwards and forwards in it should be as straightforward as moving backwards and forwards in space: to travel in time is thus simply to follow a path, which can be represented by a line joining one temporal location with another. If we want to rid ourselves of the myth of time travel, we must therefore critically examine the assumption that time is a dimension like up-down, right-left or back-front.

One thing should arouse our suspicion at once. If the dimensions of space and the dimensions of time are truly comparable, why are there three of the former (at least) and only one of the latter? And why do the spatial three look so similar, while the fourth looks very much like the odd one out? Up-and-down and back-and-forth and left-and-right are manifestly of the same kind, while before-and-after isn’t. This is evident in the way we group spatial dimensions as if they belonged together: we do not think of calling one of the spatial dimensions ‘the fourth dimension’. Time is manifestly the added-on party. What is more, time seems to be more substantial than the dimensions of space, such as length. Unlike time, length does not exist in-itself, except as an abstraction that has to be represented by a line; and that is a cheat, because the line has to have three dimensions to be visible, even if its length far exceeds its width and depth. Time seems more the equal of three-dimensional space itself than of any of the individual three dimensions of space.

A paradoxical consequence of thinking of time as a dimension on all fours with the three of space is that we are inclined to ascribe quasi-spatial properties to it which are not actually applicable even to spatial dimensions. For example, we talk about the passage or flow of time, as if it were moving, while we wouldn’t think of talking about the passage or flow of space. Indeed, we would not know what to make of the idea, because space is that within which things pass or flow. It is even suggested that, unlike space, time has a direction of flow. Philosophers have tried to find a basis for this, in, for example, the increasing overall entropy of the universe, or the relationship between cause and effect. That is to say, there is the notion of an ‘arrow of time’, which has a direction (although in what sense the arrow is in motion is never made clear) whereas the ‘arrow of space’ would not have much intuitive appeal.

The fact that time is attributed characteristics that are entirely alien to space should make one very dubious about regarding time as comparable to spatial dimensions such as height, width and depth. To say this is not to deny that time is a dimension in either the physical or mathematical sense. Nor is it wrong to represent it by a line on a graph, or to mark a point in space-time by a set of four figures related to four axes. This has been a very potent way of thinking of change, and of the mechanical laws that govern change. The mistake is to think that this quasi-spatial representation captures time in itself; to confuse a way of describing time with time as it is experienced. More precisely, those who think of time as a fourth quasi-spatial dimension are confusing Euclidean space, which has three dimensions, with Minkowskian space, which has four, but which is not the kind of space you can walk around, or travel, in.

So please let us have no more talk of time travel and its paradoxes – except in order to challenge the notion of time as a fourth dimension analogous to those of space.

Raymond Tallis is a physician, philosopher, poet and novelist. His new book Michelangelo’s Finger: An Exploration of Everyday Transcendence is published by Atlantic.

This site uses cookies to recognize users and allow us to analyse site usage. By continuing to browse the site with cookies enabled in your browser, you consent to the use of cookies in accordance with our privacy policy . X

New to Doctor Who or returning after a break? Check out our guides designed to help you find your way!

Causal nexus

A causal nexus , ( TV : Logopolis ) also called a spatio-temporal causal nexus point ( AUDIO : The Mutant Phase ), time-space nexus , temporal nexus point , causal nexus point , nexus point , or just nexus , was a place in space and time that was malleable, ( PROSE : Remembrance of the Daleks ) points in the space-time continuum that were very rare and hard to access. ( PROSE : Invasion of the Cat-People )

Where time would normally be able to resist or absorb minor changes, the Third Doctor noted that some locations in space and time were temporal probability nexuses where multiple strands of causality were exposed and weak, and the smallest alteration could produce aberrant loops of existence or even new alternate timelines . ( PROSE : The Eye of the Giant )

As related to cause and effect, i.e. causality , nexus points often served as areas for potential anomalies, since the Fourth Doctor stated that every point in time had its alternative. ( TV : Pyramids of Mars )

4 Outside time and space
5 Behind the scenes

In time [ ]

Causal nexuses existed within time fissures , which were created all the time. Though not visible, they could be sensed by time sensitives , and larger events could create fissures where time tracks diverged from the nexus point, allowing for travel to parallel universes . ( AUDIO : The Wreck of the Titan )

The Doctor's TARDIS became caught in a spatio-temporal causal nexus point when it hit a bump in the time track , generated by the Daleks of an alternate timeline using a time corridor to pull the Fifth Doctor into their future. ( AUDIO : The Mutant Phase )

The causal nexus divided when Nyssa changed history as part of the plan arranged by the Doctor's first TARDIS , causing the universe to exist in two quantum states and releasing blinovitch energy . When the time paradox was corrected with another paradox, the Fifth Doctor became the causal nexus as the paradox resulted from knowledge he would claim not to know in his personal future. ( AUDIO : Prisoners of Fate )

The Doctor reflects on the Wenley Moor Affair. ( COMIC : Final Genesis )

In keeping with this, the " Wenley Moor Affair " was a crucial nexus-point in Earth's time stream because countless futures could diverge from that moment into alternate realities. ( COMIC : Final Genesis ) Similarly, the Eleventh Doctor identified the Cwmtaff incident as a temporal tipping point which would "change future events, create its own timeline, its own reality." ( TV : Cold Blood )

The Sixth Doctor detected a temporal nexus point which turned out to be Evelyn Smythe , whose ancestors were slowly disappearing from history. ( AUDIO : The Marian Conspiracy )

The planet Chronos in 3286 was a nexus point which could have led to the creation of the Cyberverse . ( WC : Real Time )

The temporal period surrounding 1941 Earth was a crucial nexus point in the planet's development, and any alterations, such as killing Adolf Hitler , would disrupt the Web of Time . ( COMIC : Me and My Shadow )

Rose Tyler , having travelled to Donna's World , refused to reveal her name. She stated that "one word in the wrong place can change an entire causal nexus". ( TV : Turn Left )

When asked why he couldn't just take the TARDIS back to the previous day, the Tenth Doctor recited, as if by rote, "I can't go back within my own timeline. I have to stay relative to the Master within the causal nexus." He earlier called the same set of events a convergence. ( TV : The End of Time )

When the Kin 's take-over of Earth led to humanity dying out by 2010 , the Eleventh Doctor explained to Amy Pond that she still existed because she was an independent temporal nexus, "chrono-synchronistically established as an inverse...," but eventually agreed with Amy that the reason was " timey wimey ." He also referred to the divergence point in 1984 for the alternate timeline as the nexus. ( PROSE : Nothing O'Clock )

While discussing changing her personal past, Older Amy Pond capped a list comprised of destiny and causality with the nexus of time itself, a structure of causal nexus points that described or defined time. However, at the time she was referencing changing her own recent personal history from within a stable temporal anomaly that was generated artificially. ( TV : The Girl Who Waited )

In space [ ]

Causal nexuses seemed to exist as actual structures of the universe , based on planets . Earth was widely recognised as one of the causal nexus points of Mutter's Spiral . ( PROSE : Cat's Cradle: Witch Mark )

Logopolis and its inhabitants ran the Charged Vacuum Emboitements that kept N-Space going past the point of collapse. When the Tremas Master stopped Logopolis, he caused the unravelling of the whole causal nexus. This released a wave of entropy that engulfed parts of the universe, killing them. ( TV : Logopolis )

A nexus resided in the transjovian space near Jupiter , which the Hand of Omega reached using faster-than-light travel , after which traversing the nexus to reach Skaro in its own time zone by punching a hole in reality . ( PROSE : Remembrance of the Daleks )

In both [ ]

The particles of the Time Vortex could clump together at a nexus point. A TARDIS could hold onto a nexus point with mathematical anchors to resist the streaming delta flows. ( PROSE : Cat's Cradle: Witch Mark )

The Seventh Doctor considered (and blamed) Earth as a "major time-space nexus" for the reason he was on Earth at certain times and the coincidences that came from that. These included him being in Mesopotamia in the time of Gilgamesh ( PROSE : Timewyrm: Genesys ) and being in Ife during the 10th century . In the latter travel, there may have been static electricity involved which made the Yoruba believe he was Shango , the thunder god . ( PROSE : Transit )

The Edifice 's interior dimensions were mapped onto its exterior, making it the same size inside as outside, cancelling its dimensional transcendence . This also caused it to become a nexus point , affecting past and future events along the causal pathways , generating temporal anomalies in the resulting temporal pulses. ( PROSE : The Ancestor Cell )

Outside time and space [ ]

A hyper reality nexus was created by Godwanna to access hyper reality and absorb all the energy she created from destroying Earth in 1994 . ( PROSE : Invasion of the Cat-People ) There were points in the universe where parallels collided, where the Parallel Sect created a reality web threaded through the whole infinity of the universe. ( AUDIO : The End of the Line )

Behind the scenes [ ]

The term "temporal nexus point" first appeared in FASA 's The Doctor Who Role Playing Game , but was not used in a valid story until The Marian Conspiracy .

2 Time Lord
3 The Doctor

Not logged in

Contributions
Create account

Causal nexus

Create talk

Page actions

Edit source

A causal nexus , ( TV : Logopolis [+] Loading... ["Logopolis (TV story)"] ) also called a spatio-temporal causal nexus point , ( AUDIO : The Mutant Phase [+] Loading... ["The Mutant Phase (audio story)"] ) causal nexus point , ( PROSE : The Ancestor Cell [+] Loading... ["The Ancestor Cell (novel)"] ) nexus-point , ( COMIC : Final Genesis [+] Loading... ["Final Genesis (comic story)"] ) nexus point , ( COMIC : Empire of the Daleks [+] Loading... ["Empire of the Daleks (comic story)"] , etc.) temporal nexus point , ( AUDIO : The Marian Conspiracy [+] Loading... ["The Marian Conspiracy (audio story)"] ) temporal tipping point , ( TV : Cold Blood [+] Loading... ["Cold Blood (TV story)"] , Dermot and the Doctor [+] Loading... ["Dermot and the Doctor (TV story)"] ) time-space nexus , ( PROSE : Timewyrm: Genesys [+] Loading... ["Timewyrm: Genesys (novel)"] ) or simply just nexus , [ source needed ] was the opposite of a fixed point in time ; ( TV : Cold Blood [+] Loading... ["Cold Blood (TV story)"] , AUDIO : The Shadow Vortex [+] Loading... {"timestamp":"00:21:51","1":"The Shadow Vortex (audio story)"} ) they were a place in space and time that was malleable. ( PROSE : Remembrance of the Daleks [+] Loading... ["Remembrance of the Daleks (novelisation)"] )

1.3 Time and space
2.1.1 Pre-War era
2.1.2 War era
2.1.3 Post-War era
2.2 In space
2.3 In both
2.4 Outside time and space
3 Behind the scenes

Nature [ [edit] | [edit source] ]

A causal nexus existed in both space and time .

Time [ [edit] | [edit source] ]

The War Doctor described the opposite of a fixed point in time being "moments when everything can change." He explained that whole of 1961 was one such point. ( AUDIO : The Shadow Vortex [+] Loading... {"timestamp":"00:21:51","1":"The Shadow Vortex (audio story)"} )

The Eleventh Doctor described a temporal tipping point as a point that could "change future events , create its own timeline , its own reality ." ( TV : Cold Blood [+] Loading... ["Cold Blood (TV story)"] )

One account asserted that such points in the space-time continuum were very rare and hard to access. ( PROSE : Invasion of the Cat-People [+] Loading... ["Invasion of the Cat-People (novel)"] )

Nexus points existed on other planets too, such as Bav and Teth , which were also attacked by the Daleks . ( PROSE : The Dalek Problem [+] Loading... ["The Dalek Problem (novel)"] )

Space [ [edit] | [edit source] ]

more to be added

Time and space [ [edit] | [edit source] ]

History [ [edit] | [edit source] ]

In time [ [edit] | [edit source] ], pre-war era [ [edit] | [edit source] ].

The Seventh Doctor identified the Wenley Moor Affair as a crucial nexus-point in Earth 's time stream such that a countless number of futures could be claimed from that moment with near-endless divergent realities . ( COMIC : Final Genesis [+] Loading... ["Final Genesis (comic story)"] )

The Sixth Doctor detected a temporal nexus point which turned out to be Evelyn Smythe , whose ancestors were slowly disappearing from history. ( AUDIO : The Marian Conspiracy [+] Loading... ["The Marian Conspiracy (audio story)"] )

The planet Chronos in 3286 was a nexus point which could have led to the creation of the Cyberverse . ( WC : Real Time [+] Loading... ["Real Time (webcast)"] )

War era [ [edit] | [edit source] ]

During the Last Great Time War , Stasi Lieutenant Kruger assumed that the War Doctor 's claim that history would not remember men like him kindly, then Lara Zannis 's scheme could not be successful as Earth continued to exist; exasperated, the Doctor explained that the opposite was true, as the whole of 1961 , from beginning to end, was one big moment when "everything can change." ( AUDIO : The Shadow Vortex [+] Loading... {"timestamp":"00:21:51","1":"The Shadow Vortex (audio story)"} )

Post-War era [ [edit] | [edit source] ]

Rose Tyler , having travelled to a parallel world , refused to reveal her name. She stated that "one word in the wrong place can change an entire causal nexus". ( TV : Turn Left [+] Loading... ["Turn Left (TV story)"] )

The Eleventh Doctor identified the 2020 Cwmtaff incident as a "temporal tipping point", explaining that it was not a fixed point in time . ( TV : Cold Blood [+] Loading... ["Cold Blood (TV story)"] )

The Doctor also identified 26 January 2011 , the night of the National Television Awards , as a temporal tipping point; " millions of people are going to be making vitally important decisions , and if they make just one tiny mistake the entire universe will be destroyed ." ( TV : Dermot and the Doctor [+] Loading... ["Dermot and the Doctor (TV story)"] )

When time travelling Daleks failed to effectively control the Roman emperor Caligula , the Elite Guard Dalek abandoned the mission whilst noting that there were other nexus points in human history . ( COMIC : Empire of the Daleks [+] Loading... ["Empire of the Daleks (comic story)"] )

In space [ [edit] | [edit source] ]

In both [ [edit] | [edit source] ]

The Seventh Doctor considered (and blamed) Earth as a "major time-space nexus" for the reason he was on Earth at certain times and the coincidences that came from that. These included him being in Mesopotamia in the time of Gilgamesh ( PROSE : Timewyrm: Genesys [+] Loading... ["Timewyrm: Genesys (novel)"] ) and being in Ife during the 10th century . In the latter travel, there may have been static electricity involved which made the Yoruba believe he was Shango , the thunder god . ( PROSE : Transit [+] Loading... ["Transit (novel)"] )

Outside time and space [ [edit] | [edit source] ]

A hyper reality nexus was created by Godwanna to access hyper reality and absorb all the energy she created from destroying Earth in 1994 . ( PROSE : Invasion of the Cat-People [+] Loading... ["Invasion of the Cat-People (novel)"] )

There were points in the universe where parallels collided, where the Parallel Sect created a reality web threaded through the whole infinity of the universe. ( AUDIO : The End of the Line [+] Loading... ["The End of the Line (audio story)"] )

Behind the scenes [ [edit] | [edit source] ]

The term "temporal nexus point" first appeared in FASA 's The Doctor Who Role Playing Game .

Space-time anomalies
Temporal theory
Articles needing citation

Recent changes
Random page
111,947 articles

Topical pages

Last season
Latest episode
Next season
Fifteenth Doctor
Ruby Sunday
The Pantheon
Kate Stewart
Morris Gibbons
Carla Sunday
The Toymaker
Fourteenth Doctor
Donna Noble

Other useful pages

Main episode list
Regeneration
Request Videos
Help + Community Policies
Upload images
Explore special pages
Browse properties

User page tools

What links here
Related changes
Printable version
Permanent link
Page information

Hidden category

This page was last edited on 18 August 2024, at 19:14 (UTC). Last edited: 19:14, 18 August 2024 (UTC)

Content is available under CC BY-SA 3.0 unless otherwise noted.
Privacy policy
About Tardis Wiki
Disclaimers
Mobile view

[ May 9, 2024 ] Moon Phases: What They Are & How They Work Solar System
[ April 3, 2024 ] Giordano Bruno Quotes About Astronomy Astronomy Lists
[ March 28, 2024 ] Shakespeare Quotes: Comets, Meteors and Shooting Stars Astronomy Lists
[ March 28, 2024 ] Shakespearean Quotes About The Moon Astronomy Lists
[ November 30, 2022 ] The Night Sky This Month: December 2022 Night Sky

5 Bizarre Paradoxes Of Time Travel Explained

December 20, 2014 James Miller Astronomy Lists , Time Travel 58

There is nothing in Einstein’s theories of relativity to rule out time travel , although the very notion of traveling to the past violates one of the most fundamental premises of physics, that of causality. With the laws of cause and effect out the window, there naturally arises a number of inconsistencies associated with time travel, and listed here are some of those paradoxes which have given both scientists and time travel movie buffs alike more than a few sleepless nights over the years.

Types of Temporal Paradoxes

The time travel paradoxes that follow fall into two broad categories:

1) Closed Causal Loops , such as the Predestination Paradox and the Bootstrap Paradox, which involve a self-existing time loop in which cause and effect run in a repeating circle, but is also internally consistent with the timeline’s history.

2) Consistency Paradoxes , such as the Grandfather Paradox and other similar variants such as The Hitler paradox, and Polchinski’s Paradox, which generate a number of timeline inconsistencies related to the possibility of altering the past.

1: Predestination Paradox

A Predestination Paradox occurs when the actions of a person traveling back in time become part of past events, and may ultimately cause the event he is trying to prevent to take place. The result is a ‘temporal causality loop’ in which Event 1 in the past influences Event 2 in the future (time travel to the past) which then causes Event 1 to occur.

This circular loop of events ensures that history is not altered by the time traveler, and that any attempts to stop something from happening in the past will simply lead to the cause itself, instead of stopping it. Predestination paradoxes suggest that things are always destined to turn out the same way and that whatever has happened must happen.

Sound complicated? Imagine that your lover dies in a hit-and-run car accident, and you travel back in time to save her from her fate, only to find that on your way to the accident you are the one who accidentally runs her over. Your attempt to change the past has therefore resulted in a predestination paradox. One way of dealing with this type of paradox is to assume that the version of events you have experienced are already built into a self-consistent version of reality, and that by trying to alter the past you will only end up fulfilling your role in creating an event in history, not altering it.

– Cinema Treatment

In The Time Machine (2002) movie, for instance, Dr. Alexander Hartdegen witnesses his fiancee being killed by a mugger, leading him to build a time machine to travel back in time to save her from her fate. His subsequent attempts to save her fail, though, leading him to conclude that “I could come back a thousand times… and see her die a thousand ways.” After then traveling centuries into the future to see if a solution has been found to the temporal problem, Hartdegen is told by the Über-Morlock:

“You built your time machine because of Emma’s death. If she had lived, it would never have existed, so how could you use your machine to go back and save her? You are the inescapable result of your tragedy, just as I am the inescapable result of you .”

Movies : Examples of predestination paradoxes in the movies include 12 Monkeys (1995), TimeCrimes (2007), The Time Traveler’s Wife (2009), and Predestination (2014).
Books : An example of a predestination paradox in a book is Phoebe Fortune and the Pre-destination Paradox by M.S. Crook.

2: Bootstrap Paradox

A Bootstrap Paradox is a type of paradox in which an object, person, or piece of information sent back in time results in an infinite loop where the object has no discernible origin, and exists without ever being created. It is also known as an Ontological Paradox, as ontology is a branch of philosophy concerned with the nature of being or existence.

– Information : George Lucas traveling back in time and giving himself the scripts for the Star War movies which he then goes on to direct and gain great fame for would create a bootstrap paradox involving information, as the scripts have no true point of creation or origin.

– Person : A bootstrap paradox involving a person could be, say, a 20-year-old male time traveler who goes back 21 years, meets a woman, has an affair, and returns home three months later without knowing the woman was pregnant. Her child grows up to be the 20-year-old time traveler, who travels back 21 years through time, meets a woman, and so on. American science fiction writer Robert Heinlein wrote a strange short story involving a sexual paradox in his 1959 classic “All You Zombies.”

These ontological paradoxes imply that the future, present, and past are not defined, thus giving scientists an obvious problem on how to then pinpoint the “origin” of anything, a word customarily referring to the past, but now rendered meaningless. Further questions arise as to how the object/data was created, and by whom. Nevertheless, Einstein’s field equations allow for the possibility of closed time loops, with Kip Thorne the first theoretical physicist to recognize traversable wormholes and backward time travel as being theoretically possible under certain conditions.

Movies : Examples of bootstrap paradoxes in the movies include Somewhere in Time (1980), Bill and Ted’s Excellent Adventure (1989), the Terminator movies, and Time Lapse (2014). The Netflix series Dark (2017-19) also features a book called ‘A Journey Through Time’ which presents another classic example of a bootstrap paradox.
Books : Examples of bootstrap paradoxes in books include Michael Moorcock’s ‘Behold The Man’, Tim Powers’ The Anubis Gates, and Heinlein’s “By His Bootstraps”

3: Grandfather Paradox

The Grandfather Paradox concerns ‘self-inconsistent solutions’ to a timeline’s history caused by traveling back in time. For example, if you traveled to the past and killed your grandfather, you would never have been born and would not have been able to travel to the past – a paradox.

Let’s say you did decide to kill your grandfather because he created a dynasty that ruined the world. You figure if you knock him off before he meets your grandmother then the whole family line (including you) will vanish and the world will be a better place. According to theoretical physicists, the situation could play out as follows:

– Timeline protection hypothesis: You pop back in time, walk up to him, and point a revolver at his head. You pull the trigger but the gun fails to fire. Click! Click! Click! The bullets in the chamber have dents in the firing caps. You point the gun elsewhere and pull the trigger. Bang! Point it at your grandfather.. Click! Click! Click! So you try another method to kill him, but that only leads to scars that in later life he attributed to the world’s worst mugger. You can do many things as long as they’re not fatal until you are chased off by a policeman.

– Multiple universes hypothesis: You pop back in time, walk up to him, and point a revolver at his head. You pull the trigger and Boom! The deed is done. You return to the “present,” but you never existed here. Everything about you has been erased, including your family, friends, home, possessions, bank account, and history. You’ve entered a timeline where you never existed. Scientists entertain the possibility that you have now created an alternate timeline or entered a parallel universe.

Movies : Example of the Grandfather Paradox in movies include Back to the Future (1985), Back to the Future Part II (1989), and Back to the Future Part III (1990).
Books : Example of the Grandfather Paradox in books include Dr. Quantum in the Grandfather Paradox by Fred Alan Wolf , The Grandfather Paradox by Steven Burgauer, and Future Times Three (1944) by René Barjavel, the very first treatment of a grandfather paradox in a novel.

4: Let’s Kill Hitler Paradox

Similar to the Grandfather Paradox which paradoxically prevents your own birth, the Killing Hitler paradox erases your own reason for going back in time to kill him. Furthermore, while killing Grandpa might have a limited “butterfly effect,” killing Hitler would have far-reaching consequences for everyone in the world, even if only for the fact you studied him in school.

The paradox itself arises from the idea that if you were successful, then there would be no reason to time travel in the first place. If you killed Hitler then none of his actions would trickle down through history and cause you to want to make the attempt.

Movies/Shows : By far the best treatment for this notion occurred in a Twilight Zone episode called Cradle of Darkness which sums up the difficulties involved in trying to change history, with another being an episode of Dr Who called ‘Let’s Kill Hitler’.
Books : Examples of the Let’s Kill Hitler Paradox in books include How to Kill Hitler: A Guide For Time Travelers by Andrew Stanek, and the graphic novel I Killed Adolf Hitler by Jason.

5: Polchinski’s Paradox

American theoretical physicist Joseph Polchinski proposed a time paradox scenario in which a billiard ball enters a wormhole, and emerges out the other end in the past just in time to collide with its younger version and stop it from going into the wormhole in the first place.

Polchinski’s paradox is taken seriously by physicists, as there is nothing in Einstein’s General Relativity to rule out the possibility of time travel, closed time-like curves (CTCs), or tunnels through space-time. Furthermore, it has the advantage of being based upon the laws of motion, without having to refer to the indeterministic concept of free will, and so presents a better research method for scientists to think about the paradox. When Joseph Polchinski proposed the paradox, he had Novikov’s Self-Consistency Principle in mind, which basically states that while time travel is possible, time paradoxes are forbidden.

However, a number of solutions have been formulated to avoid the inconsistencies Polchinski suggested, which essentially involves the billiard ball delivering a blow that changes its younger version’s course, but not enough to stop it from entering the wormhole. This solution is related to the ‘timeline-protection hypothesis’ which states that a probability distortion would occur in order to prevent a paradox from happening. This also helps explain why if you tried to time travel and murder your grandfather, something will always happen to make that impossible, thus preserving a consistent version of history.

Books: Paradoxes of Time Travel by Ryan Wasserman is a wide-ranging exploration of time and time travel, including Polchinski’s Paradox.

Are Self-Fulfilling Prophecies Paradoxes?

A self-fulfilling prophecy is only a causality loop when the prophecy is truly known to happen and events in the future cause effects in the past, otherwise the phenomenon is not so much a paradox as a case of cause and effect. Say, for instance, an authority figure states that something is inevitable, proper, and true, convincing everyone through persuasive style. People, completely convinced through rhetoric, begin to behave as if the prediction were already true, and consequently bring it about through their actions. This might be seen best by an example where someone convincingly states:

“High-speed Magnetic Levitation Trains will dominate as the best form of transportation from the 21st Century onward.”

Jet travel, relying on diminishing fuel supplies, will be reserved for ocean crossing, and local flights will be a thing of the past. People now start planning on building networks of high-speed trains that run on electricity. Infrastructure gears up to supply the needed parts and the prediction becomes true not because it was truly inevitable (though it is a smart idea), but because people behaved as if it were true.

It even works on a smaller scale – the scale of individuals. The basic methodology for all those “self-help” books out in the world is that if you modify your thinking that you are successful (money, career, dating, etc.), then with the strengthening of that belief you start to behave like a successful person. People begin to notice and start to treat you like a successful person; it is a reinforcement/feedback loop and you actually become successful by behaving as if you were.

Are Time Paradoxes Inevitable?

The Butterfly Effect is a reference to Chaos Theory where seemingly trivial changes can have huge cascade reactions over long periods of time. Consequently, the Timeline corruption hypothesis states that time paradoxes are an unavoidable consequence of time travel, and even insignificant changes may be enough to alter history completely.

In one story, a paleontologist, with the help of a time travel device, travels back to the Jurassic Period to get photographs of Stegosaurus, Brachiosaurus, Ceratosaurus, and Allosaurus amongst other dinosaurs. He knows he can’t take samples so he just takes magnificent pictures from the fixed platform that is positioned precisely to not change anything about the environment. His assistant is about to pick a long blade of grass, but he stops him and explains how nothing must change because of their presence. They finish what they are doing and return to the present, but everything is gone. They reappear in a wild world with no humans and no signs that they ever existed. They fall to the floor of their platform, the only man-made thing in the whole world, and lament “Why? We didn’t change anything!” And there on the heel of the scientist’s shoe is a crushed butterfly.

The Butterfly Effect is also a movie, starring Ashton Kutcher as Evan Treborn and Amy Smart as Kayleigh Miller, where a troubled man has had blackouts during his youth, later explained by him traveling back into his own past and taking charge of his younger body briefly. The movie explores the issue of changing the timeline and how unintended consequences can propagate.

Scientists eager to avoid the paradoxes presented by time travel have come up with a number of ingenious ways in which to present a more consistent version of reality, some of which have been touched upon here, including:

The Solution: time travel is impossible because of the very paradox it creates.
Self-healing hypothesis: successfully altering events in the past will set off another set of events which will cause the present to remain the same.
The Multiverse or “many-worlds” hypothesis: an alternate parallel universe or timeline is created each time an event is altered in the past.
Erased timeline hypothesis : a person traveling to the past would exist in the new timeline, but have their own timeline erased.

The Metaphysical Possibility of Time Travel Fictions

Original Research
Open access
Published: 16 June 2021
Volume 88 , pages 1309–1329, ( 2023 )

Cite this article

You have full access to this open access article

Nikk Effingham ORCID: orcid.org/0000-0002-1839-7347 1

6210 Accesses

4 Citations

14 Altmetric

Explore all metrics

In some stories, time travellers cannot change the past. It is widely accepted that this is metaphysically possible. In some stories, time travellers can change the past. Many philosophers have explained how that, too, is metaphysically possible. This paper considers narratives where sometimes the past can change and sometimes it cannot, arguing that this is also something that is possible. Further, I argue that we can make sense of stories where some events appear to be ‘fixed points in time’.

Vacillating time: a metaphysics for time travel and Geachianism

Praesens de futuris: whitehead on how to be going to move forward into the future.

Norton’s Objective Temporal Passage

Avoid common mistakes on your manuscript.

1 Introduction

In some time travel stories, the past can change e.g. Kleiser’s The Flight of the Navigator ( 1986 ), Curtis’s About Time ( 2013 ), or Landon’s Happy Death Day ( 2017 ). As an example, consider Happy Death Day . The protagonist, ‘Tree’, is murdered in a tunnel. She then awakes earlier that day, having travelled in time. Tree lives through that day again, but this time things play out differently and she isn’t murdered in a tunnel. The past has changed!

In other time travel stories, the past cannot change e.g. Moorcock’s Behold the Man ( 1969 ), Gilliam’s 12 Monkeys ( 1995 ), and Vigalondo’s Los Cronocrímenes ( 2007 ). As an example, consider Los Cronocrímenes . The protagonist, ‘Hector’, sees a woman, naked in the forest. Investigating, Hector finds her unconscious, whereupon he is attacked by a bandaged man. Managing to later travel in time, it transpires that it was Hector’s later self who forced the woman to strip and who knocked her unconscious, as well as being the bandaged man. Nothing plays out differently; whilst the viewer sees the same event multiple times, it always plays out the same way.

These two types of film mirror the two main philosophical approaches to time travel: ‘Ludovicianism’ (Lewis, 1976 ), the theory that the past cannot be changed, and the ‘non-Ludovician’ theories which allow for the past to change. For each, much work has already been done to show that they are metaphysically possible (for discussion, see Effingham, 2020 ).

But some stories don’t correspond to either. In those stories, the past is sometimes changeable whilst, on other occasions it cannot be changed. This paper argues that even these time travel scenarios are metaphysically possible.

There are two reasons to be interested in whether such fictions are metaphysically possible. First reason: It builds on the project David Lewis started. David Lewis asks whether any time travel narrative is consistent ( 1976 : 145). It’s only natural to further ask exactly which sorts of narratives are consistent i.e. whether a narrative according to which the past is only changeable on occasion is possible or not. Second reason: It’s independently interesting to map what logical space is like and what sort of time travel might be permitted, regardless of its connection with fiction.

Section 2 explains the Ludovician model and how probability works in that model. Section 3 explains the hypertemporal non-Ludovician model, arguing that it’s the best non-Ludovician model for understanding most fictional stories. Section 4 moves to those time travel fictions where the past is intermittently changeable, arguing that a model ‘mixing’ Ludovicianism with hypertime can account for such fictions. Section 5 discusses ‘fixed points in time’, whereby time travellers find they can change some events but not others; I discuss how the mixed model can allow for these fixed points.

This paper does not aim to explain all problematic elements in all time travel fictions. Many will still go unexplained. Nevertheless, in the spirit of speculation, I suggest that more advanced ‘mixed models’ might help with at least some of these issues. Section 6 gives an example of a narrative which can be explained by further mixing.

2 Ludovician Time Travel

2.1 examples in fiction.

Imagine I travel back to 1930 to assassinate Hitler. The Ludovician says that I would fail to succeed. Some event would inevitably get in my way, thwarting me. I might be unable to locate Hitler, or shoot the wrong person, or simply miss when I finally have him in my crosshairs. Taking this through to its natural conclusion, I’d be unable to change anything in the past—what once was, always will be. Were this how time travel worked, all time travellers will end up in the same situation as Hector from Los Cronocrímenes , unable to change events from being the way that they previously were.

Lewis ( 1976 ) is the most famous Ludovician [for a fuller exposition and list of supporters see Effingham ( 2020 : 67–73)]. It is a theory adopted by many fictions.

Star Trek . In ‘Captain’s Holiday’ (1990), aliens from the future attempt to rescue an artefact destroyed by Captain Picard. Partially due to the efforts of the aliens, Picard ends up destroying the artefact. Another example: In ‘Time’s Arrow’ (1992) the crew travel back in time, having found Data’s head buried at an archaeological dig. Their time travelling then leads to Data being decapitated in the past and his head being left for the future crew to find.

The Terminator ( 1984 ). A soldier from a dystopic future comes back to save the mother of an unborn child who will lead the resistance against the robots that have taken over the world. The mother is saved and the future stays the same (and the solider turns out to be the biological father of the unborn child).

Harry Potter . In ‘The Prisoner of Azkaban’ (Rowling, 1999 ) the protagonists, believing (but not having seen) a friendly hippogriff killed, return in time to save it. It turns out that the hippogriff never died in the first place, due to the actions of their future time travelling selves.

Doctor Who . In ‘The Aztecs’ (1964) the Doctor avers that history cannot be changed and that the Aztecs’ practice of human sacrifice cannot be stopped.

Red Dwarf . In ‘Future Echoes’ (1988) Lister witnesses an image from the future in which one of his companions loses a tooth. To demonstrate that he can change the future, Lister tries to prevent the tooth loss. In doing so, he breaks his companion’s tooth.

These examples also neatly describe ‘causal loops’ wherein an event causes another event which causes another event, and so on, until—via the miracle of time travel—they loop back to cause the original event. For instance, finding Data’s head brings about the time travel which results in him losing his head; it’s a causal loop. Similarly, in the other examples: the time travelling soldier in The Terminator is the father of the man who sends him back in time in the first place; Lister’s attempt to stop the future happening causes it to happen; and so on.

2.2 Ludovician Probability

In Red Dwarf ’s ‘Cassandra’ (1999) the protagonists meet an oracle who knows all future facts. The oracle reveals that one character, Rimmer, will imminently die before leaving the ship, whilst the other protagonists will live for some time yet. Another character, Kryten, notes that this means that the others are now invulnerable. Taking a gun, he points it at his own head, pulls the trigger, and—against the odds—it misfires. He then does the same to the other characters fated to survive, each time amazingly failing to discharge. Shooting it in Rimmer’s direction, it fires perfectly.

This fictional example is instructive (if not entirely representative!) of how probability would function in a Ludovician time travel case (Effingham, 2020 : 147–75). To see why, imagine that when I try and kill Hitler I am committed enough to make fifty attempts before giving up. Imagine also that I am so skilful an assassin that only one of two things can prevent my success: (i) a commonplace event, out of my control, occurring every time I try; (ii) a random heart attack killing me before I even make my first attempt. (In reality, of course, there’d be more outcomes than (i) and (ii), but they will do as heuristic placeholders.)

Let the chance of me being struck down by a heart attack be one in a billion. Let the chance of a commonplace event preventing an assassination attempt be 0.05; the chance of a chain of fifty of them occurring is then 8.9 × 10 –66 . Given those probabilities, were I to try and kill a regular, presently existing, dictator, I would almost certainly succeed. The chance would be 1 − 1 × 10 –9 − 8.9 × 10 –66 i.e. roughly 1.

But when I try to kill Hitler, things are different since something will stop me—indeed, given the assumption, one of (i) or (ii) will save Hitler. As a rational Ludovician, my credence of (i) and (ii) coming about should therefore proportionately increase given that I know I will fail (Effingham, 2020 : 152–54). Since the chance of (ii) is greater, by 57 orders of magnitude, than the chance of (i), the proportionate increase means that that my expectation of dying from a heart attack should be 57 orders of magnitude greater than my expectation of a chain of coincidental events coming about. So, were I to try and kill Hitler, I should expect to die of a heart attack.

In other time travel cases, similar thoughts will apply. If I try to change the past, something will stop me and it’ll be more likely that it’s a singular—quite possibly dangerous—event which does that preventative work. Time travel is dangerous for my health!

There are two objections the Ludovician might raise.

First objection. Lewis says that the events which play the preventative role are ‘commonplace’ (Lewis, 1976 : 150). Likewise, we might think he thought the probabilities of events in time travel cases would be normal and mundane, not strange and dangerous like I’ve indicated.

But Lewis’s talk of ‘commonplace’ events just means that the things which prevent me killing Hitler needn’t be outlandish events like supernatural agents or interventionist ‘time patrols’. For Lewis, the events which stop me can be ‘commonplace’ events like my gun misfiring, or me mistaking my target, and so on. Lewis says nothing about the likelihood of such ‘commonplace’ events occurring.

Second objection. The Ludovician says that in different contexts I have different abilities. For instance, I can’t kill Hitler in 1930 in a context which assumes that he survives 1930. Ludovicians are quick to point out that the same also applies in non-time travel scenarios e.g., assuming I will fail to assassinate a contemporary dictator, then I don’t have the ability to kill them. That said, the second objection is that the same parity between abilities in time travelling/mundane scenarios should apply to probabilities . Were that so, nothing strange would be going on. Rather, when we recognise that I have a high probability of having a heart attack when I try to kill Hitler, that’s no more unusual than recognising that, assuming I would fail , I’d have a high probability of having a heart attack were I to try and kill a contemporary dictator.

But something strange is going on and what is said about abilities cannot be said of probabilities. I agree that there’s some probability function according to which I have a high probability of a heart attack both when I try and kill Hitler and when I try and kill the contemporary dictator. But that’s because probability functions are cheap and plentiful; that probability function is not the salient probability function. The probability function we should care about is the ‘rational credence’ probability function of a (presumably non-actual) well-informed agent. When you’re trying to figure out what to expect (and what actions to take), it’s that function which you’re aiming for with your own probability judgements. And since the rational credence an agent assigns to a proposition varies depending only upon what that agent believes, not the context in which the agent finds themselves in, then the function we’re interested in isn’t context sensitive in the way that ability claims are.

Moreover, the rational credence function of a well-informed agent returns the result that it’s dangerous to use a time machine to kill Hitler but not for me to attempt the assassination of a contemporary dictator. Imagine a rational agent is gambling as to whether I’ll succeed in killing a contemporary dictator. Since they’re well-informed, they know that only one of (i) or (ii) could stop me. In this case, the gambler’s well-informed body of beliefs says nothing about whether—at the future time—I succeed or fail. Thus, the gambler will say I’ll likely succeed and bet accordingly. Next, imagine we ask the gambler to bet on me succeeding in killing Hitler. Being well-informed they know that I’m using a time machine, that Hitler survived 1930, and that only one of (i) or (ii) will stop me. Given all that knowledge, it’s now rational for them to predict that my assassination attempt will fail; indeed, the gambler will instead expect me to have a heart attack. Since we want our actions and expectations to mimic those of the well-informed rational agent, we should likewise expect me to have a heart attack when attempting historical assassinations but not contemporary ones.

The question then arises: Why are time travellers faced by these dangers whilst regular assassins are not? A bad answer is to think that contemporary assassins can change the future whilst time travellers cannot change the past. It’s a bad answer because, for the Ludovician, no facts can ever change, whether they’re past, present, or future (Horwich, 1987 : 116; Lewis, 1976 : 150; Putnam, 1962 : 669). Even contemporary assassins can’t change facts about the future—they can causally affect the future, but not change it.

The correct answer instead focuses on what ‘well-informed’ consists in. In the case of killing contemporary dictators, it’d be wrong to imagine that the rational gambler has an antecedent commitment to my succeeding or failing. But in the case of me using a time machine to kill Hitler, it is appropriate to imagine the rational gambler antecedently believing that I will fail. That is: In the former case, it’s unreasonable to think my succeeding or failing is part of being well-informed, whilst in the case of me attempting to kill Hitler, it’s the other way around (Hall, 1994 : 508–9; Lewis, 1986 : 94). This, in turn, is because when I try and kill Hitler I’m involved in (or potentially involved in) a causal loop, but I’m not involved in one when I try to kill the contemporary dictator. When killing Hitler, I’m involved in (or could be involved in) a causal loop because Hitler’s surviving 1930 plays a causal role in my personal history e.g. his survival, and later heinous acts, cause me to come back to kill him. (The ‘personal history’ of an agent is that web of events which has causally influenced—i.e. affected the intrinsic properties of—the person up until that point; this includes, say, events from long before the person is born e.g. those involving their ancestors.) Since causal loops appear only in time travel cases, killing contemporary dictators doesn’t involve causal loops and so won’t come hand-in-hand with weird expectations. Wannabe assassins of Hitler, from Helmut Hirsch to Fabian von Schlabrendorff, would not have been rational to expect to be definitely thwarted in their assassination attempts. Likewise, if I time travel to the past, and also travel to a place in space so far away that my activities can’t affect my personal history, no probabilistic peculiarities will arise. Similarly, if one time travels in a non-Ludovician fashion one avoids being in a causal loop (see Section 3 ) and, if loops are avoided, no probabilistic weirdness arises. But in the causal loop case, it’s reasonable for the well-informed rational gambler to know everything about my causal history—that is part and parcel of their being well-informed. In the case of me killing Hitler, this includes my failing in the assassination attempt. In the case of the contemporary dictator, even if it turns out that I actually fail and have a heart attack, that failure isn’t part of my causal history and so it’s illegitimate for it to feature in the beliefs of the imaginary well-informed agent.

In conclusion, time travellers caught up in causal loops (or liable to get caught up in causal loops) should expect weird events to happen. In particular, they should expect a single unlikely event to prevent their changing the past. It’s not hard to reach the conclusion that the singular event might well be deleterious to one’s health and well-being. Ludovician time travellers beware!

Even apparently inconsequential events may be part of my personal history, such that interacting with them is dangerous for me. Imagine that it’s 800 AD. Sigeburg is currently enamoured of Cuthbert. But tomorrow morning, Cuthbert will yawn when he opens his door. Wandering by, Sigeburg will find this repugnant and deem Cuthbert to be an unsuitable suitor. Years later, Sigeburg will go on to marry someone else. One of their descendants will be a man who, in 1915, arrives at the navy office slightly earlier than my great-grandfather. In turn, that descendent, rather than my great-grandfather, is assigned to a vessel destroyed by U-boats. Thus, if Cuthbert does not yawn at that exact moment in 800 AD, I will not be born. I can no more stop the yawn than I could assassinate Hitler. Were I to sit talking to Cuthbert—where I might accidentally cause him to sleep in a little longer by drinking just a tad more mead, in turn causing Sigeburg to miss his romantic faux pas—I am increasing the probability of some event thwarting me doing just that. Strange probabilistic occurrences would happen, thwarting my interacting with Cuthbert. Even if I were unaware of his role in my personal history, that’d make no difference to these probabilistic issues. Talking to Cuthbert could be deadly to me.

One last note. Even non-time travellers might be caught up in these cases if they—knowingly or otherwise—start interacting with time travellers. If, for instance, I go back in time and try and trick someone into killing Hitler for me, that will increase their chances of having a heart attack. Similarly, if I go back in time to Cuthbert’s village, those around me (who I might otherwise accidentally influence into stifling Cuthbert’s yawn) will likewise be threatened by unlikely events.

2.3 Probability and Fiction

In fictions portraying Ludovician time travel, there is a tendency to see either no strange coincidences or only a very limited number. But, given Section 2.2 , this isn’t representative of how it actually would be were Ludovicianism true. Indeed, elsewhere (2020: 168) I’ve argued that the practical upshot of the probabilistic concerns from Section 2.2 is that, since any time travel to within your past light cone will likely result in some interaction (even at a sub-atomic scale!) with your personal history, any attempt to activate a time machine would likely kill you. Very few fictions represent that probabilistic fact [for exceptions, see Niven’s ‘Rotating Cylinders and the Possibility of Global Causality Violation’ ( 1977 ) and Levinson’s ‘The Chronology Protection Case’ ( 1995 )].

Two things should be said about this. First, fictions often suppress truths about the world. In Die Hard II ( 1990 ) a plane blows up when John McClane lights its trail of fuel. In reality, aviation fuel has too high a flashpoint to ignite like that. In Point Break ( 1991 ) Keanu Reeve’s character conducts a lengthy conversation whilst skydiving. In reality, this would be impossible given the loud sound of rushing wind. In numerous TV shows and movies, chloroform soaked rags almost instantly render people unconscious, far from the real world truth. Fictional depictions of Ludovician time travel similarly involve such suppression.

Second, by failing to realistically depict how probability would work in a Ludovician time travel case, time travel fictions end up depicting unlikely narratives. But ‘unlikely’ doesn’t mean ‘impossible’. If we’re interested solely in their possibility, then possible they are! (And some narratives may lend themselves to the idea that the time travellers have supraphysical powers allowing them to warp probability, avoiding these problems entirely.)

3 Non-Ludovician Time Travel

3.1 examples in fiction.

Fiction contains many examples of time travellers changing the past:

Star Trek . In ‘Yesterday’s Enterprise’ (1990) a ship comes back from the past to the future, escaping a battle. That affects the result of the battle and the future is instantly changed, becoming dystopian. Eventually, the ship returns to the past and history reverts back to how it originally was. Another example: In ‘Time Squared’ (1989) Captain Picard returns from a future disaster and then dies. The crew then change events so that this never happens.

Terminator 2 ( 1991 ). A time travelling robot comes back to 1995 from 2029. It teams up with the protagonists and they try and prevent the end of the world. We discover, in Terminator 3: Rise of the Machines ( 2003 ), that they change the future by delaying the apocalypse eight years.

Harry Potter . In ‘Harry Potter and the Cursed Child’ ( 2016 ) the protagonists travel in time and change history so that Voldemort now lives and rules the world.

Red Dwarf . In ‘Tikka to Ride’ (1989) the crew of the ship return to the past for supplies, accidentally saving JFK which ultimately results in a nuclear war. Realising their error, they recruit JFK’s future self and return to 1963 where they get JFK to assassinate himself. The nuclear war is now averted.

3.2 Universe and Hypertemporal Indexing

Prima facie , changing the past seems to be impossible. Consider some instant, t 1930 , in 1930. At t 1930 , Hitler is alive. Later, I go back in time and change things so that Hitler is now dead at t 1930 . Where P is the proposition 〈Hitler is alive〉 the following contradiction would be true:

‘Non-Ludovician’ theories of time travel solve this problem by introducing extra entities to avoid the contradiction. One model introduces extra universes (Deutsch, 1991 ). Time travel takes you back to the past, but to a universe different from that which you left. In that new universe, the time traveller can change things however they want. Just as, without fear of contradiction, it can rain at one place and not rain at another, different things can be true at different universes (since a universe is simply a very large place). On this model, if I return to t 1930 to kill Hitler then there are universes \({\mathbb{U}}_{1}\) , \({\mathbb{U}}_{2}\) … whereby I leave universe \({\mathbb{U}}_{1}\) (at which Hitler was alive at t 1930 ) to arrive at t 1930 in universe \({\mathbb{U}}_{2}\) . There, I kill Hitler. The following proposition would be true:

That proposition is no more contradictory than it raining right now (in that it’s raining in Seattle) and it not raining right now (in that New York is clear skied). So universe non-Ludovicianism solves the problem.

A spin on this theory, ‘hypertemporal non-Ludovicianism’, introduces an extra dimension of time instead of extra universes (Bernstein, 2017 ; Goddu, 2003 ; Hudson & Wasserman, 2010 ; van Inwagen, 2010 ). Hypertemporal theories vary over their specifics (e.g. whether they accept growing block theory or eternalism, whether time is fundamentally tensed or tenseless, and so on). I assume an ‘eternalist’ hypertemporal theory (Chown, 2007 ; Effingham, 2020 : 76–79; Hudson & Wasserman, 2010 ). That model assumes there are two temporal dimensions, time and ‘hypertime’. They are temporal analogues to the two spatial dimensions one would find in a flatland. Just as, in a flatland, you can go left–right and backwards–forwards, in a world with two dimensions of time there is the pastwards–futurewards direction and a hyperpastwards-hyperfuturewards direction.

Use the variables t 1 , t 2 … to refer to regular temporal instants and the variables T 1 , T 2 … to refer to hypertemporal instants. Since the two-dimensional temporal world is analogous to the spatial dimensions of flatland, each hypertime has its own complement of times. For instance, at T 1 there exist instants t 1 , t 2 … whilst t 1 , t 2 … also all exist at T 2 and at T 3 , and so on for all hypertimes (analogous to how, in a two dimensional flatland consisting of x and y spatial axes, every ‘ x point’ exists along every ‘ y point’). Time travellers travel back in the regular temporal dimension but always move forwards in the hypertemporal dimension. If I go back to kill Hitler, I leave one hypertime (e.g. T 1 ) and arrive back in 1930 but at a hyperlater hypertime ( T 2 ). It’s at that hypertime at which I kill Hitler and make the following proposition true:

Again, that proposition isn’t contradictory.

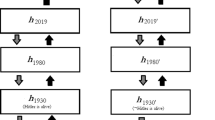
Consider a second example. In Doctor Who ’s ‘Pyramids of Mars’ [1975] the Doctor and Sarah Jane go from 1980 to 1911. In 1911, the antagonist of the story, Sutekh, conspires to wipe out all life. Sarah Jane says not to worry for, having seen the future, she knows Sutekh fails. To disprove this, the Doctor takes Sarah Jane to 1980, where Earth is now a desolate wasteland orbiting a dead sun. Witnessing the results of inaction, they return to 1911 and defeat Sutekh. 1980 then changes back to how it once was.

See Fig. 1 . The Doctor starts at one time, t 1980 . Given the hypertemporal model, he’s also at a certain hypertime, in this case T 19 . Refer to that temporal/hypertemporal location using Cartesian co-ordinates i.e. ‘ t 1980 - T 19 ’. When the Doctor travels back to 1911, he moves forward in hypertime, arriving at t 1911 - T 20 . There, he shows Sarah Jane the future by travelling to 1980. Since he moves forwards in regular time, not backwards, he stays at the same hypertime, arriving at t 1980 - T 20 . Whilst t 1980 - T 19 was nice, t 1980 - T 20 is nasty. Travelling back in time again (and, therefore, ahead in hypertime, to T 21 ) the Doctor arrives at t 1911 - T 21 . There he frustrates Sutekh’s plans. Thus t 1980 - T 21 is as nice as t 1980 - T 19 .

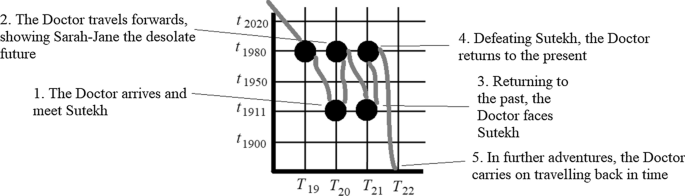
A Hypertemporal understanding of ‘Pyramids of Mars’

3.3 In Favour of Understanding Fiction in Hypertemporal Terms

It’s curious that whilst there are fictions explicitly relying on universe indexing [e.g. Baxter’s The Time Ships ( 1995 ) and Hamilton’s The Saints of Salvation ( 2020 )] examples of fictions explicitly relying on hypertemporal indexing are absent. Footnote 1

Nevertheless, it is more natural to read fictions as presenting a hypertemporal non-Ludovicianism than a universe non-Ludovicianism. This is because hypertime bests captures the motives of fictional characters. Consider ‘Pyramids of Mars’. If universe non-Ludovicianism were true, the Doctor would have little reason to act to stop Sutekh. Imagine that time travellers create new universes when they travel back in time. In one universe, 1980 is nice. In a second universe, Sutekh’s actions make 1980 nasty. The Doctor then travels to the future of that universe, shows Sarah Jane that it’s nasty, and travels back in time to stop Sutekh. Thus, the Doctor creates a third universe (in which 1980 ends up again being nice). But what was the point? I don’t ameliorate the problem of global poverty and starving children in the world by fathering some non-starving children of my own. Similarly, if the Doctor is worried about the horrible universe Sutekh brings about, he doesn’t ameliorate that problem by creating a third universe at which Sutekh has not done terrible things—all he does is create a place which is nice, not eliminate the place which is nasty. Footnote 2

Given hypertemporal non-Ludovicianism, the Doctor has much more motive to act. Standardly, we favour how things presently are. I have been in pain in the past and my presently not being in pain is preferable; when in pain, I have a motive to make my pain a mere item of the past. Were there a second temporal dimension, we should likewise prefer how things hyperpresently are. When Sutekh makes 1980 a terrible place, he makes 1980 hyperpresently a terrible place. The Doctor—seeing that this is a bad thing—puts it right and makes it the case that, hyperpresently, 1980 is a nice place. Sutekh’s devastation is relegated to being a mere item of the hyperpast; whilst there’s nothing the Doctor can do about the hyperpast being the way that it is, at least the way the world hyperpresently ends up being is better in light of his actions. He is therefore clearly motivated to change time (in a way that he isn’t, given universe non-Ludovicianism).

I suspect that similar reasons apply to understanding other fictional narratives. We’re best advised to treat most fictional cases of the past changing as being cases of hypertemporal non-Ludovicianism.

4 The Mixed Model

For both Ludovician and non-Ludovician time travel, the same fictions have been used as examples i.e. Star Trek , Harry Potter , The Terminator , Red Dwarf , and Doctor Who . In those narratives, the characters can sometimes change time whilst, on other occasions, time travel results in a Ludovician causal loop with no change possible. This section deals with how to allow for the possibility of such narratives.

It can be allowed if we tinker with the hypertemporal model. The vanilla hypertemporal theory from Section 3 has it that time travellers always move forwards to hyperlater hypertimes when they travel back in time. Drop that stipulation. Whilst, in some cases, people ‘merely time travel’ (by going back in time and moving forward in hypertime), in other cases they can also ‘hypertime travel’ and go back to hyperearlier hypertimes (or, alternatively, manage to stay at the one they are hypercurrently at whilst nevertheless travelling back into the ‘regular’ past).

If hypertime travel is allowed, we run straight back into the original problem we were faced with. Imagine I ‘merely time travel’ from 2020 to 1930 and kill Hitler i.e. I travel from t 2020 - T 1 to t 1930 - T 2 and make it the case that Hitler’s dead at t 1930 - T 2 . If I have a hypertime machine, I can then travel from t 2020 - T 2 to t 1930 - T 1 . Can I then kill Hitler there?

One solution is to redux the same move the hypertemporal theorist made in the original case i.e. add an extra dimension of time. Adding in an ‘ultratemporal’ dimension, which hypertime machines always move forward in, it’d turn out that Hitler’s alive at t 1930 - T 1 at one ultratime and dead at t 1930 - T 1 at an ultralater ultratime.

But scotch that suggestion. The crux of this paper’s theory is that, in the example fictions, this isn’t what happens. Instead, when someone hypertime travels, that hypertemporal travel ends up being ‘Ludovician’. Were one to go back in hypertime to t 1930 - T 1 then one would fail to assassinate Hitler. Just as commonplace events like guns misfiring and mistaken identities save Hitler from assassination given regular Ludovicianism, the same sorts of events will occur to prevent Hitler from being assassinated at T 1 were someone to hypertime travel back to that point. Footnote 3

Call this the ‘mixed model’. If, like myself, you think both Ludovician and non-Ludovician time travel are metaphysically possible, there’s little reason to think that this mixed model is not also possible. And, given its possibility, we can allow for fictions wherein sometimes time is changed and sometimes it isn’t. Consider three examples.

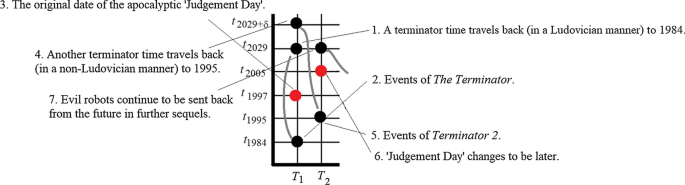
Figure 2 depicts the narrative of The Terminator . At the first hypertime, T 1 , the protagonist, ‘Reese’, and the Terminator both travel in a Ludovician manner from 2029 back to 1984. Reese then becomes the father of the man who sends him back in time. Slightly later in 2029, t 2029+δ , (and at the same hypertime, T 1 ) another terminator is sent back in time. But in this case, it is in a non-Ludovician manner. Because the time travel is non-Ludovician, that terminator arrives in the past (in 1995) at a hyperlater hypertime, T 2 . That terminator can make time different from how it hyperwas at T 1 . The events of Terminator 2 then play out and the protagonists delay the apocalypse occurring by eight years.

The mixed model understanding of The Terminator/Terminator 2

As another example, consider (some of) the narrative of Star Trek , namely the events of ‘Yesterday’s Enterprise’ followed by the events of ‘Time’s Arrow’. See Fig. 3 . This time, the non-Ludovician time travel comes first and the Ludovician time travel comes second. At T 1 , the Enterprise-C is involved in a battle in 2344 and is destroyed. Later, at that same hypertime, the Enterprise-D (led by Captain Picard) somehow disturbs a portal into the past, affecting the past in a non-Ludovician manner. This allows the Enterprise-C through to the future, t 2367 , at a hyperlater hyperinstant, T 2 . The history of T 2 is changed by this event to be different than that of T 1 and the world, from t 2344 onwards, is more dystopian. The events of ‘Yesterday’s Enterprise’ then take place and the crew of the future convince the crew of the past to return back to the past and put right what once went wrong. So there is yet more non-Ludovician time travel as the Enterprise-C returns to the past (at t 2367+ δ ) at another, hyperlater, hypertime, T 3 . The past is now put aright and 2367 is no longer dystopian at T 3 .

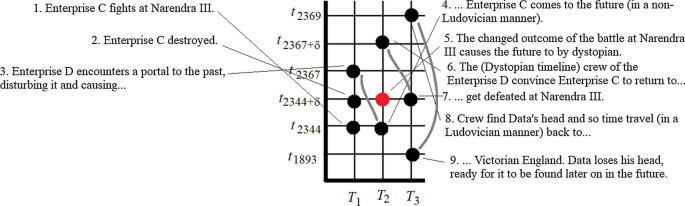
The mixed model understanding of Star Trek

Later on, at T 3 , the crew—at t 2369 —come across Data’s head. Using a time machine, they travel back to 1893, but this time in a Ludovician manner—that is, they time travel back within the same hyperinstant. There, Data loses his head. Since that takes place at the same hyperinstant, the head can later be discovered by the crew at t 2369 - T 3 , creating the causal loop depicted in ‘Time’s Arrow’.

Both these examples involve causal loops arising from hypertime travel within the same hyperinstant. I’ve argued elsewhere (2020: 22–24) that travelling within the same instant is a type of time travel; similarly, to travel within the same hypertemporal instant is to hypertime travel. But there are also clearer cases of hypertime travel where causal loops stretch between hypertimes. I’ll use Red Dwarf as an example, although similar loops appear elsewhere, e.g. in Harry Harrison’s The Stainless Steel Rat Saves the World ( 1972 ), Baxter’s The Time Ships ( 1995 ), and various episodes of Doctor Who (e.g. ‘The Name of the Doctor’ ( 2013 ) and, indeed, mostly any episode where multiple Doctors meet one another).

See Fig. 4 , which depicts three cases of time travel in the Red Dwarf narrative. The first is the Ludovician causal loop from the episode ‘Future Echoes’. At one time, t 3m , Lister sees an event from the future and tries to stop it, which then causes it to happen later at t 3m+1 .

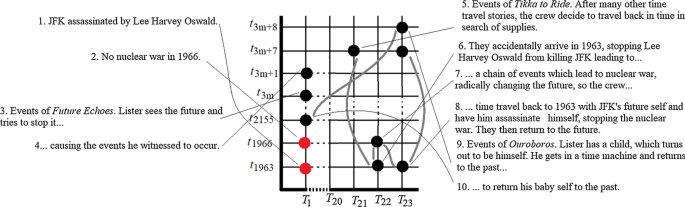
The mixed model understanding of Red Dwarf

The second case is the events of ‘Tikka to Ride’. Marooned three millions years into deep space (at t 3m+7 - T 21 ) the crew decide to return to the past for supplies. Accidentally arriving in 1963 (at t 1963 - T 22 ) they prevent Lee Harvey Oswald from killing JFK. Trying to escape the police, they travel forwards in time (to t 1966 - T 22 ) where they discover JFK’s survival has led to a nuclear war. Realising their mistake, they recruit JFK’s future self and travel back to 1963 (to t 1963 - T 23 ) where they get JFK to assassinate his past self. History is, more or less, put back to how it hyperwas (except for the fact that Oswald no longer killed JFK and instead JFK killed JFK). Red Dwarf is thus a mixed model.

The third case is a causal loop stretching back in hypertime. In a later episode, ‘Ourorobos’ (1997), Lister has a child. It transpires that the child is Lister [so Lister is a ‘bootstrapped’ person ( cf Effingham, 2020 : 59–65)]. Baby Lister is then returned to the past to become the adult Lister. The clear implication of the narrative is that these events have not changed time i.e. it is not that, hyperpreviously, Lister was a regular person born to regular parents but that, from T 22 onwards, he is instead his own father. Rather, the implication is that throughout the entire show he has always been his own father. Thus, Lister must have returned back to the original hypertime he was born at, t 2155 - T 1 , and left his baby self to be found by his adoptive parents. That requires going back to a hyperprevious hyperinstant. (And note that, since it involves a causal loop, we get the same probabilistic issues discussed in Section 2.3 ; we should, again, appreciate that whilst the narrative of ‘Ouroboros’ is possible, it’s therefore nevertheless very unlikely.)

5 Fixed Points

5.1 examples in fiction.

With the mixed model in place, turn to consider another feature common to time travel narratives: ‘fixed points’. In Simon Wells’ The Time Machine ( 2002 ), Dr. Alexander Hartdegen’s fiancé is killed by a mugger. To save her, Hartdegen invents a time machine, changes the past, and saves her. However, she is then run over by a carriage. Hartdegen realises that no matter what he does, he’ll be unable to stop her from being killed—every time she is saved, she’ll simply die in a different manner. Her dying can be changed in certain respects (e.g. from her being killed in a mugging to being killed in an accident) but not others (e.g. she must always die at roughly that time). Her death is a ‘fixed point in time’.

At first glance, there seems to be no room for fixed points in the mixed model. When Hartdegen travels back in time, he travels forwards in hypertime, so what’s stopping Hartdegen from preventing his fiancé’s death at that hyperlater hypertime? If Hartdegen can change time so his love isn’t shot but run over, why can’t he change time such that she lives to an old age? Why are events fixed in some respects but not others? This problem is compounded later in the film. Hartdegen travels to 802,701 AD and, further again, to the cataclysmic future of 635,427,810 AD. He then returns to 802,701, changing the future so the apocalypse is averted. The questions arises: Why can Hartdegen change that future but not that of his fiancé? How come some events are ‘fixed’ whilst other events are ‘unfixed’?

That some events are ‘fixed’ and others are ‘unfixed’ is a common trope in time travel fiction. Usually ‘major historical’ events are fixed and only more minor events are ‘unfixed’. Examples include:

Various episodes of The Twilight Zone . In ‘Back There’ (1961) the protagonist is unable to stop Lincoln’s assassination, whilst still finding themselves able to nevertheless change certain things. In ‘The Time Element’ (1958) the protagonist tries to stop the bombing of Pearl Harbour, finding himself unable to do so, but does manage to change history and cause himself to cease to exist. In ‘Memphis’ (2003) the protagonist tries to stop Martin Luther King’s assassination, failing to do so, but managing to change the past in other respects.

Fixed points routinely feature in Doctor Who . In ‘Earthshock’ (1982), Adric dies and the Doctor refuses to go back in time and save him. Even though the Doctor regularly changes historical events in other stories, there is something about this event which means he won’t try. In ‘The Visitation’ (1982), the Doctor accidentally starts the Great Fire of London but recognises that it must be let to run its course. Given the fire causes large amounts of property damage and kills six people—outcomes which the Doctor causes and intentionally allows to happen—that’s somewhat uncharacteristic of the Doctor. Presumably, he puts out other fires he accidentally starts, so what’s so special about this fire? In ‘The Water of Mars’ (2009) the Doctor appears on Mars in 2059, meeting the first astronauts on the red planet. He knows that the astronauts he meets there are going to die. When talking to one of the astronauts, Adelaide, he is quite explicit, saying that ‘Certain moments in time are fixed. […] those certain moments, they have to stand […] What happens here must always happen.’ When the Doctor tries to prevent Adelaide’s death, he still fails for she ends up unexpectedly committing suicide.

In Supernatural ’s ‘In the Beginning’, Dean is sent back in time to 1973. Whilst history can be changed in some respects, Dean is unable to save his mother from being murdered. It is explained to him ‘Destiny can’t be changed […] All roads lead to the same destination.’

Fixed points play a crucial role in the plot of Connie Willis’s To Say Nothing of the Dog ( 1997 ).

5.2 Fixed Points and Ludovician Probability

There is a way to make sense of fixed points within the mixed model. In the fixed point cases, unlikely things are happening. In The Time Machine the fiancé is—against the odds—run over by a carriage. And, taking Hartdegen at his word, the suggestion is that whatever action he takes to save her, some event will nevertheless kill her anyhow. In Doctor Who , Adelaide’s suicide is something which is unexpected and prima facie unlikely to have happened. Similarly, random occurrences prevent the derailing of history in The Twilight Zone episodes. These unlikely events sound similar to the unlikely events from Section 2 ’s regular Ludovician cases. In the one-dimensional Ludovican case, when I go to kill Hitler, a low probability event occurs to stop me i.e. a heart attack. This unlikely event comes about because I am interacting with things in my personal history. In the mixed model, the same interactions can arise and in such cases we should expect strange issues with probability to likewise arise on the mixed model. It is these issues with probability which explain why certain things seem to be ‘fixed’.

To understand what’s going on, we first must introduce ‘immanent causation’. There are two types of causation (Zimmerman, 1997 : 433ff). The first is the regular ‘transeunt’ causation we are well acquainted with e.g. I flick a switch which then causes a light to turn on. The second is immanent causation, which concerns something being a way at one time causing how it is at a later time. For instance, an electron being stationary and unmoving will, if it remains undisturbed, immanently cause itself to be stationary and unmoving at later times. Or if I prod an indelible mark on myself, it will remain on my body because of how my earlier body was.

Immanent causation plays an important role in hypertemporal models. Hyperlater hypertimes are how they are because they have been immanently caused to be that way by how hyperearlier hypertimes hyperwere. In a hypertemporal world in which no time travel takes place then, for every time t n , whatever is true at t n at one hypertime is true of it at every hyperlater hypertime. And in a hypertemporal world where I travel back in time to kill Hitler at t 1930 - T 2 then, whilst t 1930 is different from how it was at T 1 , it’s still mainly the same. For instance, how things are in the Andromeda galaxy are unaffected—a similarity explained by immanent causation i.e. how the Andromeda galaxy hyperwas at t 1930 - T 1 immanently causes it being that way at t 1930 - T 2 .

Immanent causation between hypertimes can feature as one of the links in a causal loop. Imagine someone travels back in both time and hypertime, going from t 2500 - T 10 to t 2020 - T 9 and causally interacting with what they find there. The qualitative features of t 2020 - T 9 immanently cause t 2020 - T 10 to be a certain way. Assuming that t 2020 - T 10 ′s changed features saliently affect the time traveller at t 2500 - T 10 then the time traveller’s travelling to the earlier/hyperearlier point results in a causal loop, with one of the links of that loop resulting from that inter-hypertemporal immanent causation. And, just as regular Ludovician travellers should expect weird probabilistic things to happen in causal loops, our imagined hypertime traveller should expect likewise. We can take this insight and use it to explain what’s going on with fixed points, although it does require some embellishment to the fictional narratives we are presented with.

Consider Simon Wells’ The Time Machine . If we thought it took place in a world of hypertime, then, given the narrative as it is explicitly presented, there would be no causal loop. See Fig. 5 a. Hartdegen is in 1903 at one hypertime. He travels back in time to 1899 to save his fiancé, moving forward in hypertime. He fails to save her and then travels onwards to 802,701 and then on, again, to 635,427,810. He then travels back in time (and, therefore, forward in hypertime) in order to prevent the apocalyptic future he’s witnessed. As Fig. 5 a makes clear, there is no causal loop.

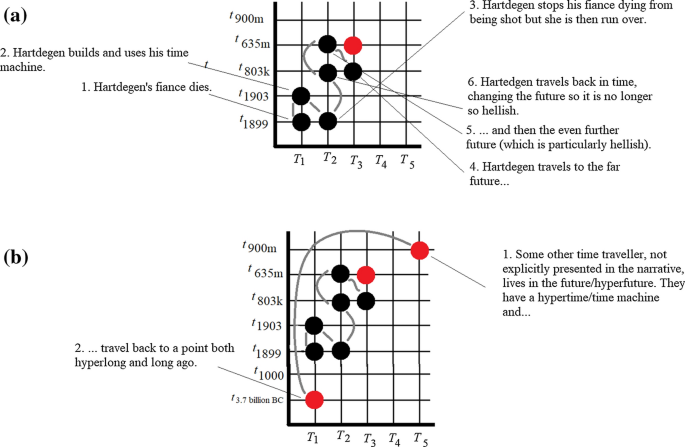
a The Time machine: The unembellished narrative. b The time machine: The embellished narrative

But if we embellish the narrative, we get a causal loop—and once we get the causal loop, we can explain the fixed point. Imagine an agent, ‘Agent’, travels from a time and hypertime both later and hyperlater than that explicitly shown in Hartdegen’s story. As an example, imagine that Agent starts all life on Earth, four billion years ago and at the earliest hypertime. See Fig. 5 b. Agent only exists at t 900m -T 5 because, five billion years earlier at t 3.7 Billion BC - T 5 , life formed on the planet. But life formed at that point only because it formed at that point in time at earlier hypertimes e.g. at t 3.7 Billion BC - T 4 (which is in turn because it formed at t 3.7 Billion BC - T 3 , t 3.7 Billion BC - T 2 , and t 3.7 Billion BC - T 1 ). So, ultimately, Agent only exists because of a causal loop they started! Notice, also, that Agent also needs Hartdegen to time travel as well. Hartdegen prevents the future from being apocalyptic; had it not been for Hartdegen, Agent would never have been born either.

Given this causal loop, we can explain why points in time appear ‘fixed’. Hartdegen would never have travelled in time if not for the death of his fiancé. Indeed, even when he saves her from the mugger, had she not then been killed in the carriage accident, he would’ve remained in the twentieth century at T 2 and never ended up travelling to the future (and, thus, never have prevented the apocalyptic future of 635,427,810). So some unlikely events will transpire to ensure that Hartdegen keeps time travelling until he ultimately prevents the apocalyptic future, in turn allowing Agent to travel back to t 3.7 Billion BC - T 1 (an event which itself ensures Hartdegen comes into being). So whilst Hartdegen can change the circumstances of his fiancé’s death, because her dying spurs him on to change the future, she will always end up dying. Her dying no matter what Hartdegen does, and the unlikelihood of events which bring that about, are exactly the same as Section 2 ’s example where Hitler always survives my concerted attempts to kill him.

Consider another example. Return to the fiction of Doctor Who . Again, embellish the narrative such that the Doctor is part of a causal loop. The Doctor comes from the race of Time Lords. Imagine that the Time Lords came into existence at some point early in both time and hypertime e.g. t 999 - T 1 . Now embellish the narrative. Imagine that Time Lords from the future/hyperfuture, e.g. t 4000 - T 500 , come back in time/hypertime and interact with their earlier/hyperearlier ancestors e.g. travelling to t 1000 - T 1 to help their ancestors invent time travel. To distinguish the Time Lords of t 4000 - T 500 from their ancestors of t 1000 - T 1 , call them ‘Future Lords’. Footnote 4

Having interfered with events at t 1000 - T 1 , the Future Lords have affected the personal history of every Time Lord from t 1000 - T 1 onwards. Since causation is transitive, events which causally influence the Future Lords coming back from t 4000 - T 500 are likewise in the personal history of every Time Lord. As with Section 2 ’s regular Ludovicianism, strange issues with probability only arise when time travellers are interacting with their own personal history. So when the Doctor is interacting with events which don’t form part of his personal history—and, therefore, don’t form part of the personal history of the Future Lords—unlikely events are not to be expected. But, scattered throughout space, time, and hypertime, there will presumably be events which are in the personal history of the Future Lords. And any Time Lord who would interact with such events threatens (possibly deadly!) events befalling them (in just the same way that if I go back in time to Sigeburg and Cuthbert I risk deadly events befalling me). Thus, Time Lords must be careful when travelling through history and hyperhistory, ensuring that they avoid these events and stick just to influencing those events outside of their personal histories.

Personal historical events are the ‘fixed points’ which the Doctor (usually) tries to avoid interacting with. To interact with them would put him in danger, as well as those around him. Add further that the Time Lords are bestowed with some ability to forewarn them when they’re in the periphery of their personal history (a useful ability to have if you’re going to time travel willy-nilly!) and we would then have what we see on screen: the Doctor would have a preternatural awareness that some events should not be interacted with and he would stay well away from them. He would avoid trying to alter Adric’s death, avoid interacting with his own past, sense that some events (e.g. the Great Fire of London) must be let to run their course, and so on.

So we can make sense of fixed points in the mixed model, as long as we suitably embellish a narrative. Fixed points are events in one’s personal history where interaction with them brings about unlikely events. In Hartdegen’s case, they are events which transpire to keep his fiancé dead in order to ensure that he travels to the future and prevent an apocalypse. These events can be compared to similar cases in the regular Ludovician model, whereby unlikely events thwart my every effort to kill Hitler. In the Doctor’s case, he presumes that they are events which are dangerous and so he seeks to avoid them; he won’t try to stop fixed points because he fears what might happen if he did. They can be compared to the worry in the regular Ludovician model whereby I should fear that I would die were I to try and kill Hitler in 1930 (and that, therefore, I should not attempt to assassinate him). In the case of other fictions, I suggest that similar thoughts would apply (given, of course, similar embellishments to the narratives).

6 Extensions of the Programme

The mixed model helps make sense of some time travel fictions which have otherwise been thought to be metaphysically impossible. The model, though, doesn’t make sense of every fiction. For instance, in some fictions time changes ‘gradually’ and people pop in or out of existence as ‘the timeline changes’ (see, e.g., Red Dwarf ’s ‘Timeslides’). Or the past may change but it might take time for the ‘changes to catch up to the present’ (see Effingham [Forthcoming] for discussion). Such phenomena won’t be explained by the mixed model.

But some time travel fictions which are not be explained by the mixed model can nevertheless be explained by a suitable extension of the model. Return to Section 3.2 ’s explanation of ‘Pyramids of Mars’. Given there are fixed points, that explanation now looks flawed. Sutekh changes the future so that 1980 is a wasteland—if the future is a wasteland then (in 2059) Adelaide will never be alive in order to die. If the Doctor has to worry about fixed points, why doesn’t Sutekh? Isn’t it impossible for Sutekh to change the future such that Adelaide doesn’t exist? Moreover, the Doctor seems to think that the Time Lords are threatened by Sutekh, which makes little sense given that the Future Lords are definitely going to exist in the future/hyperfuture. If the Doctor knows about the Future Lords (and the fixed points which arise because of what they’ve done), wouldn’t the Doctor know that Sutekh’s efforts were futile?

By introducing a more complicated mixed model, these problems can be solved. Take the mixed model and mix it again with the non-Ludovician hypertemporal theory, adding in a third dimension of time, ‘ultratime’. Whilst travel through time and hypertime is easy, imagine that travelling forwards in ultratime is either very difficult or generally proscribed; ultratime travel is very rare indeed. (And assume that backwards ultratime travel, i.e. travelling back to ultraearlier ultrainstants, is impossible.) Sutekh either has resources that make moving forward in ultratime a mere trifle or he obeys no proscription against moving forward in ultratime. Using ‘ \({\mathscr{T}}\) s’ to represent different ultratemporal instants, imagine that the narrative of ‘Pyramids of Mars’ starts at ultratime \({\mathscr{T}}_{1}\) . At \({\mathscr{T}}_{1}\) Sutekh knows full well what history, and hyperhistory, is like i.e. it’s a history/hyperhistory which favours his enemies, the Time Lords. Upon escaping, Sutekh moves forward in ultratime to \({\mathscr{T}}_{2}\) . Now Sutekh can change history/hyperhistory however he wants, making it into a wasteland devoid of life. At \({\mathscr{T}}_{2}\) , there are no Time Lords intervening with their earlier selves and no fixed points like Adelaide’s death. Sutekh has free reign to do whatever he wants with no fear of unlikely events thwarting his actions.

Either ignoring the general proscription on ultratime travel (because of the severity of the situation) or somehow utilising the fact that Sutekh is moving forward in ultratime to also allow himself to do similar, the Doctor travels to join Sutekh at \({\mathscr{T}}_{2}\) . There he arrives (at some hypertime) at 1980, showing Sarah Jane the desolate solar system. Then, when the Doctor returns to 1911, he again travels forward in ultratime, to \({\mathscr{T}}_{3}\) . At \({\mathscr{T}}_{3}\) , he changes things so that history/hyperhistory goes back to much the same way it was at \({\mathscr{T}}_{1}\) (i.e. the Time Lords are back to being supreme, life isn’t extinguished from the twentieth century onwards at the appropriate times/hypertimes, etc.).

This also explains why the Doctor is at such loggerheads with Sutekh. Sutekh threatens the Time Lord’s history in a way that a more ordinary time traveller could not hope to. An ordinary time traveller, who travels through merely time and hypertime, cannot wipe the Time Lords from existence (in the same way that, given regular Ludovicianism, Hitler should have no fear of me killing him in 1930). But ultratemporal time travellers can wipe the Time Lords from existence.

It’s also worth noting why the Time Lords might not want to ultratime travel (and either proscribe it or, purposefully, make it difficult). How the world is, right now, immanently causes how it is later. If nothing acts to change it, it will forever remain the same. Similarly, if all of history is a certain way and no agents have used time machines to move forward in hypertime, then for the rest of hypereternity, all of history will be the same way. If not for time travellers, every hypertemporal instant would be the same as the hyperearlier hyperinstant. Finally: If all of history/hyperhistory is a certain way, and no agents have used machines to travel forward in ultratime, then at every subsequent ultratime it’ll turn out that history/hyperhistory is exactly the same. Having tweaked history/hyperhistory to be exactly how they like it, the Time Lords will want to make sure no-one travels forward to the next ultratime to muck it up. If you want to ensure that all of history/hyperhistory remains exactly how you prefer, both ultranow and ultraforevermore (i.e. at every subsequent ultratime from the one you’re ultrapresently at), then you’ll make efforts to prevent people using ultratime machines. For instance, you’d track down scurrilous rogues like Sutekh looking to make history/hyperhistory different by ultratime travelling. Only by doing this can you make the world ultraeternally how you want it.

Thus, another iteration of mixing the mixed model with non-Ludovicianism allows us to make sense of this narrative. More generally, there will be other fictional narratives which might not be captured by the mixed model but could be captured by more sophisticated models including yet more dimensions of time. (Indeed, we might ‘mix again’ with something other than the hypertemporal theory i.e. mix the mixed model with universe non-Ludovicianism, or the theory I discuss in Effingham [Forthcoming].)

DC Comics features ‘hypertime’. However, it’s a mere MacGuffin, rather than anything related to the theory described above.

Alternatively, universe non-Ludovicianism may not involve the creation of universes but the navigation of a pre-existing set of universes. But in the same way that you don’t solve the problem of starving children by booking a flight to somewhere where there aren’t any starving children, the Doctor again fails to ameliorate Sutekh’s actions by travelling back to 1911. All he does is move himself to a place where it’s not his problem.

That time machines may have both Ludovician and non-Ludovician ‘settings’ is something which was suggested to me by Sara Bernstein when discussing her MOP view of time travel [Bernstein 2017 ].

Such interactions are very dangerous, as we learnt in Section 2.2 . But assume that on this occasion they either ‘got lucky’ or otherwise developed some method to warp probability and purposefully avoid such dangers.

12 Monkeys . (1995). [Film] Directed by Terry Gilliam. Universal Pictures.

Google Scholar

About Time . (2013). [Film] Directed by Richard Curtis. Universal Pictures.

Baxter, S. (1995). The Time Ships . New York: HarperCollins.

Bernstein, S. (2017). Time travel and the movable present. In Keller (ed.) Being, freedom, and method: Themes from the philosophy of Peter van Inwagen , Oxford University Press.

Chown, M. (2007). Time gains an extra dimension, New Scientist 2625 (Published 13 October 2007).

Deutsch, D. (1991). Quantum mechanics near closed timelike lines. Physical Review D, 44 , 3197–3217.

Article Google Scholar

Doctor Who . (1963)-Present. [Tv series] Created by Newman, Webber, and Wilson. UK: BBC Studios.

Die Hard II . (1990). [Film] Directed by Renny Harlin. USA: 20 th Century Fox.

Effingham, N. (2020). Time travel: Probability and impossibility . Oxford: Oxford University Press.

Book Google Scholar

Effingham, N. (Forthcoming). Vacillating time: A metaphysics for time travel and geachianism. Synthese . https://doi.org/10.1007/s11229-021-03108-5 .

Goddu, G. (2003). Time travel and changing the past: (Or how to kill yourself and live to tell the tale). Ratio, 16 , 16–32.

Hall, N. (1994). Correcting the guide to objective chance. Mind, 103 , 505–517.

Hamilton, P. (2020). The Saints of Salvation . London: MacMillan.

Happy Death Day . (2017). [Film] Directed by Christopher Landon. Blumhouse Productions.

Harrison, H. (1972). The Stainless Steel Rat Saves the World . London: Sphere Science Fiction.

Harry Potter and the Cursed Child . (2016). [Theatre] Written by Thorne, J., Rowling, J., and Tiffany, J. Premiered Palace Theatre, London.

Horwich, P. (1987). Asymmetries in time: Problems in the philosophy of science . Cambridge, MA: MIT Press.

Hudson, H., & Wasserman, R. (2010). Van Inwagen on time travel and changing the past. Oxford Studies in Metaphysics, 5 , 41–49.

Levinson, P. (1995). The Chronology Protection Case, Analog Sept. 1995 Edition.

Lewis, D. (1976). The paradoxes of time travel. American Philosophical Quarterly, 13 , 145–152.

Lewis, D. (1986). Philosophical papers: (Vol. II) . Oxford: Oxford University Press.

Los Cronocrímenes . (2007). [Film] Directed by Nacho Vigalondo. KarboVantas Entertainment.

Moorcock, M. (1969). Behold the Man . UK: Allison & Busby.

Niven, L. (1977). Rotating cylinders and the possibility of global causality violation, Analog 102, reprinted in Niven’s Convergent Series . New York: Del Rey.

Point Break . (1991). [Film] Directed by Kathryn Bigelow. USA: 20 th Century Fox.

Putnam, H. (1962). It ain’t necessarily so. The Journal of Philosophy, 59 , 658–671.

Red Dwarf . (1988)-. [Tv Series] Created by Grant Naylor. UK: Paul Jackson Productions.

Rowling, J. (1999). Harry Potter and the Prisoner of Azkaban . London: Bloosmbury.

Star Trek . (1966)-. [TV series] Created by Gene Roddenberry. USA: Paramount Television.

Supernatural . (2005-Present). [Tv series] Created by Eric Kripke. USA: Warner Bros. Television.

Terminator 2: Judgement Day . (1991). [Film] Directed by James Cameron. USA: TriStar Pictures.

Terminator 3: Rise of the Machines . (2003). [Film] Directed by Jonathan Mostow. USA: Sony Pictures Releasing International.

The Terminator . (1984). [Film] Directed by James Cameron. Orion Pictures.

The Flight of the Navigator . (1986). [Film] Directed by Randal Kleiser. Walt Disney Pictures.

The Time Machine . (2002). [Film] Directed by Simon Wells and Gore Verbski. Warner Bros Pictures.

The Twilight Zone . (1959–1964). [Tv Series] Created by Rod Serling. USA: CBS Productions.

van Inwagen, P. (2010). Changing the past. Oxford Studies in Metaphysics, 5 , 3–28.

Willis, C. (1997). To Say Nothing of the Dog . London: Orion Books.

Zimmerman, D. (1997). Immanent causation. Philosophical Perspectives, 11 , 433–471.

Download references

Acknowledgements

I am particularly grateful to the two anonymous referees for Erkenntnis . Their comments were both extensive and exceedingly helpful. Further thanks goes to Sara Bernstein, Tyler Collins, Isabel Finn, Iain Law, and the attendees of my presentation of this paper at the University of Birmingham.

Author information

Authors and affiliations.

School of Philosophy, Theology, & Religion, University of Birmingham, Birmingham, B15 2TT, UK

Nikk Effingham

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nikk Effingham .

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Effingham, N. The Metaphysical Possibility of Time Travel Fictions. Erkenn 88 , 1309–1329 (2023). https://doi.org/10.1007/s10670-021-00403-y

Download citation

Received : 02 December 2019

Accepted : 18 March 2021

Published : 16 June 2021

Issue Date : March 2023

DOI : https://doi.org/10.1007/s10670-021-00403-y

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Find a journal
Publish with us
Track your research

Table of Contents
Random Entry
Chronological
Editorial Information
About the SEP
Editorial Board
How to Cite the SEP
Special Characters
Advanced Tools
Support the SEP
PDFs for SEP Friends
Make a Donation
SEPIA for Libraries
Entry Contents

Bibliography

Academic tools.

Friends PDF Preview
Author and Citation Info
Back to Top

Backward Causation

Sometimes also called retro-causation. A common feature of our world seems to be that in all cases of causation, the cause and the effect are placed in time so that the cause precedes its effect temporally. Our normal understanding of causation assumes this feature to such a degree that we intuitively have great difficulty imagining things differently. The notion of backward causation, however, stands for the idea that the temporal order of cause and effect is a mere contingent feature and that there may be cases where the cause is causally prior to its effect but where the temporal order of the cause and effect is reversed with respect to normal causation, i.e., there may be cases where the effect temporally, but not causally, precedes its cause.

The idea of backward causation should not be confused with that of time travel. These two notions are related to the extent that both agree that it is possible to causally affect the past. The difference, however, is that time travel involves a causal loop whereas backward causation does not. Causal loops for their part can only occur in a universe in which one has closed time-like curves. In contrast, backward causation may take place in a world where there are no such closed time-like curves. In other words, an ordinary system \(S\) taking part in time travel would preserve the temporal order of its proper time during its travel, it would keep the same time sense during its entire flight (a watch measuring \(S\)’s proper time would keep moving clockwise); but if the same system \(S\) were to become involved in a process of backward causation, the order of its proper time would have to reverse in the sense that the time sense of the system would become opposite of what it was before its back-in-time travel (the watch will start to move counter-clockwise). So neither backward causation nor time travel logically entails each other and time travel is distinct from back-in-time travel.

2.1 Time and Backward Causation

2.2 Affecting the Past

2.3 Distinguishing Cause from Effect

2.4 the bilking argument.

2.5 Free Will

3.1 The Bootstrap Paradoxes

3.2 the consistency paradoxes, 3.3 the newcomb paradox, 4.1 the wheeler-feynman absorber theory, 4.2 tachyons, 4.3 quantum mechanics, 4.4 two alternatives, other internet resources, related entries.

The philosophical debate about backward causation is relatively new. Only little consideration of the problem can be found in the philosophical literature before Michael Dummett and Anthony Flew initiated their discussion in the mid 1950s. The reason for this is twofold. No empirical phenomena seem to demand a notion of backward causation for our understanding of them. And for a long time it was thought that such a notion involved either a contradiction in terms or a conceptual impossibility. David Hume’s definition of the cause as the one of two events that happens before the other thus rules out that the cause can happen after its effect. Moreover, according to Kant’s idea of synthetic a priori truth the claim that the cause temporally precedes its effect was considered to state such a truth. In 1954 Michael Dummett and Anthony Flew had a discussion about whether an effect can precede its cause. Dummett defended the idea whereas Flew argued that it involved contradictions in terms.

Two years later, Max Black (1956) presented an argument against backward causation, which became known as the bilking argument, and later attempts to meet the argument seemed to generate all kinds of paradoxes. Imagine \(B\) to be earlier than \(A\), and let \(B\) be the alleged effect of \(A\). Thus, we assume that \(A\) causes \(B\), even though \(A\) is later than \(B\). The idea behind the bilking argument is that whenever \(B\) has occurred, it is possible, in principle, to intervene in the course of events and prohibit \(A\) from occurring. But if this is the case, \(A\) cannot be the cause of \(B\); hence, we cannot have backward causation. Since then philosophers have debated the effectiveness of the bilking argument in particular and, in general, the validity and the soundness of the concept of backward causation.

In the 1960s and 1970s, physicists began to discuss the possibilities of particles travelling with a speed greater than light, the so-called tachyons, and as a consequence a similar debate about paradoxes involving backward causation arose among them. In case superluminal particles, like tachyons, exist and could be used to generate signals, it seemed possible to communicate with the past because tachyons going forward in time with respect to one set of reference frames would always be seen as travelling backwards in time from another set of reference frames.

Now and then physicists and philosophers also invoke backward causation in order to explain some experimental and theoretical results within quantum mechanics. For instance, this might be in connection with understanding quantum entanglement after several experiments have proven the violation of Bell’s inequalities.

2. Philosophy

A general notion of backward causation raises two sets of questions: those concerning conceptual problems and those that relate to empirical or physical matters. Among the first sets of questions that require a satisfactory answer are the following:

Can metaphysics provide a notion of time that allows that the effect precede its cause? Answering this question, one may argue, on the one hand, as Maudlin (2002, p. 184) does, that in case we allow backward and forward causation to be parts of our description of the world, the “metaphysical picture of the past generating the future must be abandoned, and along with it the mathematical tractability of local theories.” On the other hand, one may argue, as Evans (2015) among others does, that backward causation is not “precluded by the known structure of reality.” Indeed, Evans’s claim presupposes that the future is ontologically on par with the past and that basic physical laws are time symmetric such that the influence of a physical process may under certain special conditions reach backwards in time.

A proper notion of backward causation requires that the future is just as real as the present and the past. It is common among metaphysicians to distinguish between three different views on time. The first is presentism . This view claims that only events that exist now really exist. Past or future events do not exist. Past events have ceased to exist, whereas future events are yet to become real. So only statements about the present or related to the present have a definite truth value. The second view is possibilism according to which both past and present events exist, but future events are still only possible or non-existing. This view is sometimes called the growing block universe . As a consequence, the view holds that only statements about past and present events have a definite truth-value, but statements about the future are either probably true or may completely lack any truth-value. Finally, the third view is called eternalism , also named the block universe . This position maintains that every past, present and future event tenselessly exists at a certain time and that statements about these events therefore have a definite truth-value at every other time.

Usually, presentism and the growing block universe are associated with the dynamic view of becoming. The transient now plays an ontological role as the ever changing time in which things become real or perhaps, if you are a presentist, cease to exist. One reason to prefer the growing block universe from presentism may be the analysis of forward causation. In order for a present event to be caused by a past event, the past event must exist. Nothing, which does not exist in the past, can cause something that presently exists. By the same token, if the backward causation is a conceptual possibility, something must exist in the future in order for it to cause something in the present.

Thus, backward causation demands eternalism or a static account of time in the sense that there is no objective becoming, no coming into being such that future events exist on the par with present and past events. It means that the future is real, the future does not merely consist of unrealised possibilities or even nothing at all. Ordinarily we may think of the past as a nothing that once was a something. But when asked what makes sentences about the past true or false, we would probably also say that it is the facts of the past that make present sentences about the past either true or false. The fact that I went to the cinema yesterday makes it true today when I say that I went to the cinema yesterday. This view is a realist one with respect to the past. If backward causation is to be conceptually possible, it forces us to be realists with respect to the future. The future must contain facts, events with certain properties, and these facts can make sentences about the past/future true or false. Such a realist account is provided by static and tenseless theories of time. Eternalism is such a theory and holds that the participation of time into the past, the present and the future depends on the perspective we human beings put on the world. The attribution of pastness, presentness and futureness to events is determined by what we take to exist at times earlier than and times later than the time of our experience. (For further discussion, see the entry on being and becoming in modern physics .)

2.2 Affecting the Past?

Does backward causation mean that a future cause is changing something in the past? Talking about forward causation we think of the cause as the event that produces its effect or brings it about. It is not part of our notion of forward causation that the cause changes anything in the future. A cause determines what the effect will be. Regardless of whether one is an advocate for presentism, the growing block universe, or eternalism, one never considers the cause as an event that will make the future different from what it will be. Indeed, without the forward-directed cause the future would have been different from what it is going to be.

Even most protagonists consider it an unwarranted consequence that the notion of backward causation, if consistent, involves the idea that the future is able to change the past. Their answer has therefore usually been that if we have the power to bring something about in the past, what came about really already existed when the past was present. We have to make a distinction between changing the past so it becomes different from what it was and influencing the past so it becomes what it was. A coherent notion of backward causation only requires that the future is able to have an influence on what happens in the past. Nonetheless, we can say, quite parallel to forward causation, that the past would have been different if the backward-directed cause had not made the past as it turned out to be.

Can the cause be distinguished from its effect so that the distinction does not depend on a temporal ordering of the events ? For a long time the distinction between cause and effect was their temporal order. This view goes at least back to Hume who claimed, “We may define a cause to be an object followed by another, and where all the objects, similar to the first, are followed by objects similar to the second,” which is to say that “[…] if the first object had not been, the second never had existed” (Hume, [1748] 2007, 56). Although Hume did not explicitly say so, the expression “followed by” has always been read as “temporally followed by” and not “causally followed by”. So the adherents of this definition have usually tried to give an account of causation in which the cause and the effect are seen as temporal regularities between types of events. But we can also see that Hume himself added a counterfactual statement about causation which cannot be derived from his temporal definition. Apparently, he noticed that if we have a cause and an effect, there exists a relationship between them that is not given by the temporal order.

What is required for backward causation to be possible is some account of the direction of causation which does not rely on the direction of time. Various alternative proposals refer to counterfactuals, probabilities, agency, manipulation and intervention, common cause or causal forks. Among these it seems that only a Humean notion of causation explicitly makes a temporal identification of the cause and the effect. But there are also problems with some of the other accounts.

For example, it is quite common to follow David Lewis and define causation in terms of counterfactuals (Lewis, 1973). Assume event \(c\) causes event \(e\), then we have a situation in which both \(c\) and \(e\) occur, and in which the counterfactual statement “If \(c\) had not occurred, then \(e\) would not have occurred” is true. Thus, in Lewis’s view, \(e\) is causally dependent on \(c\) if, and only if, \(e\) is counterfactually dependent on \(c\). According to the traditional theory, formulated by Lewis and Stalnaker, any counterfactual statement is true if the consequent is true in the closest possible world to the actual world in which the antecedent is true. Apparently, Lewis’ definition delivers a non-temporal causal asymmetry, since the effect \(e\) is counterfactually dependent on the cause \(c\).

As we saw above, Hume also believed that causal statements entail counterfactuals, but the question is whether causal statements are definable in terms of counterfactuals. Here is an objection against such an attempt: Consider the following example. Because of severe frost during the night, ice covers the lake this morning. So, given the circumstances, if it had not been severe frost, there would not have been any ice on the lake. However, in these circumstances, the frost as the cause of the ice seems to be not only causally necessary for the ice, but the frost also seems to be causally sufficient for the ice cover. In other words, given the actual circumstances, it seems correct to say that the frost is causally sufficient as well as necessary for the ice. If we are going to represent causally sufficiency in terms of a counterfactual statement, we might then say that, given the actual circumstances, if no ice had covered the lake this morning, there would not have been a severe frost during the night. But if one accepts this objection, it shows that causal statements cannot be defined in terms of counterfactuals because such a definition does not give us the wanted asymmetry between cause and effect since each is counterfactually dependent on the other.

Sometimes this problem is called the Problem of Effects . According to this problem, the effect does not distinguish itself other than temporally from the cause because both the cause and the effect are counterfactually dependent on each other. Over the years several attempts have provided solutions to this problem. Lewis himself proposed some criteria consisting of a hierarchy of possible worlds such that a world in which \(c\) occurs but \(e\) does not occur is closer to the actual world than a world in which \(c\) does not occur due to the absence of \(e\). But a number of philosophers have challenged the aptness of these criteria, among others Bennett (1974); Faye (1989); Horwich (1993); Baker (2003); Choi (2007); Wasserman (2015), and Seli (2020).

However, and more importantly in the present context, is that Stalnaker-Lewis’ theory of counterfactuals has difficulties with backtracking counterfactuals and backward causation because if \(c\) occurs later than \(e\), the proposed method of truth evaluation assumes that \(e\) occurs in the relevant possible worlds in which \(c\) does not occur. In general, the assessment of a counterfactual conditional is carried out by assuming that the possible world must be identical with the actual world up to \(c\). Therefore, it is stipulated that the closest possible world is one in which everything happens just as in the actual world up to the time of \(c\)’s occurrence, which means, given \(e\) occurs before \(c\), that the possible world will include the occurrence of \(e\). But then it is necessarily true that there is never a possible world closer to the actual world which includes \(c\) but not \(e\). This creates a problem because we consider any causal connection between \(c\) and \(e\) as contingent. Rather we would expect that if we face a case of backward causation where both a present event \(c\) and a past event\(e\) occur, the following counterfactual would be true: “If \(c\) had not occurred, then \(e\) would not have occurred.” The truth evaluation of this counterfactual, if it were to represent backward causation, would require that the closest world without \(c\) is also one without \(e\). Nevertheless, the traditional theory does not allow such an evaluation.

How else can causality be specified so that the order of the cause-effect relationship is not time-dependent? Several possibilities seem open for such an account. Here we shall just mentioned some. One could hold that the cause makes the effect more probable in the circumstances; one could argue that causation can be understood in terms of manipulation and intervention; one could argue that we can specify causation in terms of transmission of information or conserved physical quantities. Or, finally, one could argue that causality is a primitive notion that may imply, or be used to explain, regularities, counterfactuals, probabilities, transmission of signals, or manipulation and intervention, but it cannot be completely analyzed in any of these terms. If we take into consideration that higher animals show a sense of causation, it may be a good indication that the origin of this notion goes back in history and that it stems from the cognitive evolution of grasping in which ways one’s environment is stable and in which ways one’s behavior can interact and change the environment.

This observation may come close to Lewis much later analysis of causation as influence (Lewis, 2000). Thus, it is through our ability to influence our environment that we improve our ability to manipulate and intervene in the cause of events and through which we receive knowledge of causal relationships and the causal order of this relationship (Faye, 1989; Woodward, 2003). However, such an understanding of causation is already rather complex, building on our capacity of foreseeing the effect of our own actions, on our capacity of foreseeing the effects of others’ actions, on our understanding the cause of others actions, and on our understanding the cause of physical events (Gärdenfors, 2006, p. 41).

Can the bilking argument be challenged in such a way that the mere possibility of intervention does not generate any serious paradoxes? The bilking argument is due to Max Black (1956) who assumed the following scenario. Suppose Houdini makes a prediction about the outcome of, say, a coin about to be flipped \(B\) before someone actually does the flipping \(A\). We may also assume that in the past Houdini rarely failed in his predictions. In this case we might be tempted to say that the Houdini’s answer is caused by the later flipping. But, as Black argued, after Houdini’s prediction of \(B\), we can always intervene such that the coin is not flipped or arranged opposite to Houdini’s prediction. The implication is that \(A\) seems both to be the cause and not to be the cause of \(B\). Black also argued that if \(A\) is the cause of \(B\), then the causal antecedents of \(A\) are independent of \(B\). Hence, if we cannot, after \(B\) has occurred, prevent \(A\) from happening, then \(A\) cannot be said to be causally independent of \(B\). But since it is in human power to intervene with respect to \(A\), Black concluded that \(A\) cannot be the cause of \(B\)

Since manipulation and intervention is so central for our knowledge of causal relations, the image of our capability of intervening in the course of backward causation, after the alleged effect has occurred, seems to violate the whole idea that the notion of backward causation is coherent. However, the force of the bilking argument can, it seems, be weakened in various ways.

First, one may hold that it is not a problem for our notion of backward causation that we can in principle intervene in the course of the events. Usually, we find out whether two events are causally connected trough manipulation and intervention. In case we can produce one event \(Q\) by bringing about another \(P\), or we can obstruct one event \(Q\) by preventing another \(P\), we think that \(P\) is the cause of (\(Q\). Likewise, we believe that if \(P\) causes \(Q\) in the relevant circumstances, we may be able to prevent \(Q\) from happening if we intervene in the causal order after \(P\) occurs by changing some of these circumstances, which make \(P\) causing \(Q\). Should \(Q\) occurs in spite of this intervention, there must under the new circumstances be another event \(X\) rather than \(P\) that causes \(Q\).

Now, the bilking argument holds that backward causation is impossible because we can always intervene after we have observe that the alleged effect occurs and obstruct the alleged cause from occurring. Since nothing prohibits us from doing this whenever we want, it demonstrates that backward causation does not take place. Indeed, if we actually intervene and prevent \(A\) after \(B\) has occurred, then of course a particular later \(A\) (which does not exist) cannot be the cause of a particular earlier \(B\) (which exists). But in all those cases where nobody actually intervenes, events of the same type as \(A\) may be the cause of events of the same type as \(B\). This situation is not different from what may happen in some cases of forward causation. Assume that \(P\) causes \(Q\) in the relevant circumstances. We may still prevent a particular \(P\) from happening, but at the same time a particular \(Q\) may nevertheless occur because in the given circumstances it is caused by another event than \(P\).

Second, if a later event \(A\) really causes an earlier one \(B\), then it would be impossible to intervene into the cause of the event after \(B\) has happened and therefore impossible to prevent \(A\) from happening. If someone tries, she will by all means fail. It may intuitively sound strange as long as we think of backward causation as consisting of something we can control directly by our everyday actions. But if backward causation is a notion that is applicable only to processes that human beings are unable to control in any foreseeable way the notion would not provoke our intuitions so much.

But even if we would have full control of backward causal processes and able to intervene in their cause of events, we may not, in such cases where we actually intervene, exclude backward causation from taking place. Assume someone tosses a coin a minute after the magician Houdini has predicted whether it would be heads or tails. Furthermore, assume that Houdini’s predictions are highly correlated with the outcomes of the tossed coin. Presumably, no such high correlation would exist unless we were facing a case of backward causation. However, it turns out that the construction of a correlation may behave differently depending on whether we consider Houdini’s predictions to be purely physical events or to have a semantic content.

In an example like the one mentioned it is reasonable to think that we discover the correlation between Houdini’s predictions and the subsequent outcomes of the tossed coin by comparing the semantic content of the predictions with one of the two iconic sides of the coin that define the semantic content. The side facing up determines whether the prediction is true or not. First, in order to establish a causal correlation between the content of the predictions and the outcome of the tosses we would look for a high percentage of correct statements made by Houdini. This is an epistemically necessary condition for establishing a causal correlation. Second, there cannot ontologically be a causal correlation between the semantic content of Houdini’s prediction and the (reading of) outcome of the head or tail if no flipping of the coin takes place. His predictions would not carry any truth-value and we would think of them as pure guesses. Hence, when someone attempts to bilk this experiment, he or she will either arrange the outcome opposite to the content of Houdini’s prediction or abstain from flipping the coin.

However, one might suggest that a possible reply to Black’s bilking argument is to say that both tossing the coin and preventing the toss may backwardly cause Houdini’s behavior. That the preclusion of the coin from being tossed may be a cause of Houdini’s response has also been proposed by Brian Garrett (2020). But he argues, in contrast to the scenarios described below, that the lack of flipping the coin may be the direct cause of the Houdini’s earlier prediction (because of backward causal preemption) and not only the cause of an earlier lack of prediction. Thus, it seems at least consistent to argue that both the toss and the prevention could cause Houdini’s earlier behavior regardless of whether this behavior is a prediction or the lack of a prediction, but only as long as we consider both actions to be physical events. Indeed, if we solely consider Houdini’s prediction (regardless of its semantic content) or his lack of prediction as purely physical events and do the same with the actions “tossing the coin” and “preventing tossing the coin,” we may have a high correlation of these physical events.

Thus, it seems that we have three scenarios in which we can observe backward causation even though in two of them one may attempt to bilk the cause after the alleged effect has occurred.

Scenario 1: The experimenter asks Houdini to predict the outcome of a tossed coin a minute later. It turns out that there is a high positive correlation between Houdini’s answers and the actual heads or tails.

Scenario 2: The experimenter now asks Houdini to make his predictions, but arranges the coin such that it shows heads or tails opposite to Houdini’s pronouncements. In this case, there will be a negative correlation between the semantic content of his answers and the outcome of the tosses. (Indeed, you could also arrange the outcome so there would be no correlation at all.) But one could still argue that the very fact that Houdini did not abstain from responding was because the physical act of handling the coin automatically prompted him to produce an answer. One will observe a high positive correlation between Houdini making physical pronouncements and the physical handlings of the coin, although there exists a negative or no correlation between the semantic content of his answers and the outcomes in the form of heads and tails.

Scenario 3: The experimenter asks Houdini to make his predictions. However, he abstains in situations where someone subsequently prevents the coin from flipping, but in situations where no one intervenes; there is a high correlation between his predictions and the outcomes. In those cases where someone prevents the coin from being flipped, and Houdini therefore abstains from saying anything, there cannot be any correlation between the truth-value of Houdini’s answers (since he does not produce any). However, there still seems to be a high correlation between his behaviors (i.e. the physical lack of responses) and the subsequent prevention of any outcome.

For those reasons one may argue that the bilking argument is not as powerful as Max Black might have thought.

2.5 Free will

Does backward caution imply fatalism? An often advanced objection against backward causation is that if eternalism and backward causation are possible, then the future is already determined. And if it is already determined now what the future is going to be, then it does not matter what an agent will do, since everything in the future is set and done. An agent cannot do other than what the future is determined to be. Although this argument seems very appealing, it may not hold for a closer scrutiny.

Being an eternalist one may distinguish between a determined future and a determinate future. Also this pair of concepts have different names in the literature. Sometimes determinism is called physical determinism , causal determinism or nomological determinism , whereas determinateness is named logical determinism , temporal determinism , or block determinism . A future event is determined now if and only if a present event is causally or nomologically sufficient for it to happen. In contrast, a future event is determinate with respect to the present if and only if this event occurs tenselessly at a future time. Thus, eternalists will say that an agent still has a choice to make tomorrow about whether or not she will go and see her parents, because no present event causally determined her choice tomorrow. Her choice is nevertheless determinate, and therefore it is true today what she will do tomorrow.

The discussion of free will has a long history and the overwhelming parts of this discussion has been dedicated to the problem that if the world is completely governed by deterministic laws, does it then make sense to talk about free will? Indeed, the outcome of this discussion very much depends on how we understand the notion of free will. Usually the concept of free will connects to whether or not a human agent could have done otherwise. Some philosophers, the compatibilists, believe that as long a human agent is not subject to any external or internal forces, that individual is free to do whatever he or she wants. But then the compatibilists have to dismiss some part of the following argument of consequence .

We cannot change the past.
We cannot change the laws of nature.
Hence, we cannot change either the past or the laws of nature (by 1 and 2).
If determinism is true, then our present actions are necessary consequences of the past and the laws of nature.
Hence, if determinism is true, then we can do nothing now to change the fact that our present actions are necessary consequences of the past and the laws of nature (by 4).
Hence, if determinism is true, then we cannot change that our current actions occur (by 3 and 5).
Hence, if determinism is true, then we have no power to do things differently than what we do (by 6).
Free will requires a power to do things differently.
Hence, if determinism is true, then we do not have free will (by 7 and 8).

The non-compatibilist will argue that we have free will in the sense that we could have done otherwise. Hence determinism cannot be true.

Indeed, the compatibilist will accept (1), because even an advocate of backward causation does not claim that the past can be changed. Moreover, the compatibilist does not have to accept backward causation. Most likely the compatibilist will not challenge the non-compatibilist by saying that we may be able to influence the past. It is much more likely that the compatibilist will object to the argument either by saying that not all laws of nature are deterministic or by saying that the brain operates based on ceteris paribus laws including a clause of the absence of external and internal forces. For the compatibilist this suffices to say that the agent could have done otherwise. In other words, the compatibilist’s objection would usually not concern the determinateness of the past.

As we can see, the above argument of consequence combines determinateness of the past and determinism of laws. Whatever the compatibilist would object in order to reject the argument of consequence, the argument cannot be used mutatis mutandis to argue against eternalism or the block universe, because in contrast to the discussion of free will and the past that focuses on determinism, the discussion of free will and the future focuses on determinateness. For even if indeterminism is true, i.e. if some processes of nature are indeterministic, one could still argue in favor of the block universe as some of its advocates pointed out long time ago (See Grünbaum, 1967, 28–35). Therefore, the argument against backward causation based on free will has to be different from the one posed against traditional fatalism. It has to look something like this:

If backward causation is possible, then the future has to be determinate.
If the future is determinate, it is now the case that a wanted action occurs at a later time t or it is now the case that it does not occur at this later time t (by 1).
If it is now the case that a wanted action occurs at a later time t or it is now the case that it does not occur at this later time t , I cannot perform a wanted action that does not occur at this later time t .
Hence if I cannot form a wanted action at a later time t , then I cannot be free to do otherwise (2 and 3).
Now, assuming that the future is determinate.
Hence, I am not free to do otherwise (by 4 and 5).
Hence, I have no free will.
However, I know from experience that I could have done otherwise.
Hence, the future is not determinate.
Hence, backward causation is not possible.

A common criticism has been that if the agent’s actions tomorrow are determinate, and it is therefore true today that the agent, say, will visit her parents, then the agent cannot do anything other than visit her parents. However, this conclusion seems to be a non sequitur . In order to reach such a conclusion, one must tacitly assume that the agent’s action causally determines the outcome of her choice, whereas the argument were believed to show that backward causation violates the notion of free will.

In contrast, the eternalist could argue that the reason why it is true today that an agent will visit her parents tomorrow is because the agent makes a decision that causally determines her visit before she goes to see them. If the agent makes the opposite decision tomorrow, it will be true today that she will not visit her parents. Whatever she chooses tomorrow, it will be her decision which makes it true today that she is going to see her parents. The outcome of her decision tomorrow is determinate not because the present truth value fixes her decision but because her future outcome fixes the present truth value. (Nor is it the case that the outcome of her decision causally determines her previous decision.) Thus, the eternalist may argue that even though the future is determinate, it does not exclude people from having free will. If people have free will, the argument goes, the fact that the outcome of their future decision is determinate with respect to the past does not affect their ability to choose freely.

3. Paradoxes

Of all the philosophical problems to which backward causation (and time travel) gives rise, the paradoxes are those that have generated the most heat in both physics and philosophy because, if they are valid, they exclude backward causation from being both metaphysically and logically possible. The paradoxes can grossly be divided into three kinds: (1) Bootstrap paradoxes involve a causal or information loop; (2) Consistency paradoxes involve generating a possible inconsistency; and (3)Newcomb’s paradox seems to foreclose free will. So if backward causation (and time travel) should be logically possible, one has to show that the paradoxes can be resolved and that therefore arguments based on them are invalid.

The bootstrap paradoxes arise in cases where you have a causal chain consisting of particular events in which \(a\) causes \(b, b\) causes \(c\), and \(c\) causes \(a\). The problem here is that the occurrence of \(a\) presupposes the occurrence of \(c\); in other words, the cause presupposes its effect. But how can something be required of what itself requires? Indeed this seems paradoxical. Some philosophers therefore think that this makes the idea of causal loops incoherent. Hugh Mellor even believes that

the possibility of causal loops can be excluded a priori , and so therefore can the closed timelike paths entailed by closed time, backward time-travel and all kinds of backward causation. (1991: 191).

His proof goes like this. Take four chains of events. Each of them consists of three particular events \(a, b\), and \(c\), all different tokens of the same kind of events \(A, B\) and \(C\). We then construct the chain such that

\(b \Rightarrow c \Rightarrow a\)
\({\sim}b \Rightarrow{\sim}c \Rightarrow{\sim}a\)
\(b \Rightarrow c \Rightarrow{\sim}a\)
\({\sim}b \Rightarrow{\sim}c \Rightarrow a\)

The first two sequences may be called G-chains and the other two H-chains. Moreover, Mellor assumes that all tokens of \(A, B\) and \(C\) are distributed among the four chains so that the number of chains is exactly the same, namely one fourth of the sequences. Mellor then defines a causal relation between two singular events \(a\) and \(b\) in terms of a situation \(k\) which makes \(b\) more likely to occur given \(a\) than without \(a\), i.e., \(\rP(b\mid a) \gt \rP(b\mid {\sim}a)\). But we can see that the number of chains in which \(b\) is combined with \(a\) is equal to the number of chains in which \(b\) is not combined with \(a\). In fact we have that \(\rP(b\mid a) =\) \(\rP({\sim}b\mid {\sim}a) =\) \(\rP(b\mid {\sim}a) =\) \(\rP({\sim}b\mid a)\). From this it follows that a particular \(b\)’s chance in \(k\) cannot increase with respect to \(a\) compared to its chance without \(a\). Hence \(a\) cannot affect \(b\), and therefore causal loops are impossible.

Some philosophers have not found this argument very convincing. Faye (1994) has pointed to the following problematic issues. First, Mellor measures the probability of singular events (propensities) instead of the probability of certain kinds of events. Second, he does not differentiate between circumstances in which a \(B\) is followed by an \(A\) and those in which a \(B\) is not followed by an \(A\). The argument is valid only if it can be proved, and not be stipulated, that (1) and (3) happen surrounded by the same facts. Many people would say that in a world of (1) must be different from a world of (3) in some other important respects than merely containing \(a\) or \({\sim}a\), especially since Mellor claims that the argument is valid for deterministic situations as well. Third, the equal distribution of the various chains seems quite selective. In Mellor’s G&H world, in which the number of the four chains is equal, and therefore in which the probabilities are equal, there cannot be any causal relationship between the individual \(b\) and the individual \(a\) due to the fact that the occurrence of \(a\) or \({\sim}a\) happens under exactly the same circumstances given \(b\). Finally, fourth, it seems appropriate to claim that any negative argument, like Mellor’s, should be able to show that what holds true of one world can be proved to hold true of every other world similar in all relevant respects, but in which G-chains and H-chains are not equally distributed.

It is clear that any world which contains G-chains rather than H-chains does not show the same inconsistency as Mellor’s G&H-world does. If it can be proved that causal loops in such worlds are consistent with the adopted definition, then causal loops are possible. In other words, if we set up a consistent model in which \(A\) increases the probability of \(B\), and \(B\) increases the probability of \(A\), we have then proven that causal loops are possible and that Mellor’s argument is invalid. The claim is therefore that both

\(\rP(A\mid B) \gt \rP(A\mid {\sim}B)\)
\(\rP(B\mid A) \gt \rP(B\mid {\sim}A),\)

can be shown to be true with respect to a world containing \(A\)s and \(B\)s. Assume the following probabilities, which hold for the distributions among \(A, {\sim}A, B\), and \({\sim}B\), are

On the basis of the definition of the conditional probability, we get

Thus (i) and (ii) are both true with respect to the stated world; hence we have proven, according to Mellor’s own definition of causality, that it is consistent to talk about causal loops. Mellor has not been able to establish any satisfying a priori argument against causal loops or backwards causation.

Moreover, even if one assumes that Mellor were correct in ruling out causal loops a priori , he may be wrong in holding that this impossibility entails the impossibility of time travel as well as backward causation. Mellor’s argument presupposes that it is the same kind of processes obeying the same kind of macroscopic physical laws which enters into both the forward and backward part of the causal loop. This assumption may hold for time travel but not for backward causation.

The consistency paradoxes arise when you, for instance, try to kill your younger self by a backward causal process but evidently have to fail. The reason why you must fail is quite obvious. Your younger self belongs to the past and therefore, since you cannot change the past, you cannot commit retro-suicide. This answer tacitly assumes that resurrection is impossible. You may, of course, kill your younger self in the past without changing the past if you have come alive again later on. This is not what is paradoxical. What is paradoxical is the fact that you are assumed to be able to kill your younger self in the sense that you are well-equipped to make these kinds of retro-killings, you may even be targeting your younger self, but you must always miss. The same holds, indeed, for all those people who stay alive into the present. You cannot retro-kill somebody yesterday who is alive today. There must be certain constraints which prohibit you from making retro-suicide or retro-killing, and these constraints may be very local, changing from case to case, or they may be universal in nature depending on some physical laws. So, on the one hand, the assumption is that it physically possible for you to kill somebody in the past; but, on the other hand, it is physically impossible for you to do what is physically possible. This is the paradox.

A way out of the paradox was suggested by David Lewis (1976) who argued that the ability of killing somebody should be understood as a possibility compossible with the relevant fact. As an opera singer, for example, you are able to sing operas, since you have the physical capacity and training to do so, but because of a temporary loss of voice, you cannot hum a single tune. What you can do relative to one set of facts, is something you cannot do relative to another set of facts. This contextual solution explains why you are able to retro-kill your younger self, given the fact that your gun is in proper working-order, you have a good aim at your target, and no one forces you to abstain from taking action. But it also explains why you are unable to retro-kill anybody who is alive today because you cannot change the past. The consistency paradox exists only in virtue of an equivocation of a context-sensitive ‘can’, and if we notice that, we see that the paradox vanishes like dew before the sun.

Some may reply that we are still talking about different abilities. In contrast to the case in which the opera singer sometimes cannot sing, your attempt to carry out retro-suicide inevitably fails. The opera singer is able to sing operas because he has shown it before and can demonstrate it again, but the attempted retro-killer has not proved and can never prove his ability. Therefore you are never in a situation where you can kill your younger self. If we accept this objection, we may reformulate the solution by saying that the contextual solution explains why you should be able to retro-kill your younger self under the appropriate circumstances. But, again, how can we talk about the ability to make retro-suicide relative to certain facts at all, if there are no possible worlds in which you carry out your deed. It seems reasonable to say that you have the ability to do something if there is a possible world in which you carry out this action. This is true of the opera singer. He can sing operas because he does it in a possible world in which he has not lost his voice. But you cannot make retro-suicide because there is no possible world in which you kill your younger self. You are unable, even in principle, to do so.

In sum, the consistency paradox is no paradox as long as you do not insist on changing the past. You are unable to change the past, and therefore you are unable to retro-kill anybody who is alive when you try to kill them. The paradox seems to arise only because you wrongly believe that you are able to do something you are unable to do.

Now if there is no paradox on the conceptual level, what then is it that makes retro-suicide physically impossible? It could be either local facts or global facts. Local facts that could constrain your action of retro-killing are many. Your hand was shaking while firing your gun, you got a fly in your eye, you were disturbed by a cat, you just fainted, etc. These constraining facts seem reasonable by themselves; they could have happened independently of your overall capacity of killing somebody in the past, but also in the actual situation interact with your ability and turn the action into an unsuccessful event. The problem is merely that such an explanation looks suspicious. It is a general fact that we cannot retro-kill anybody who is alive after the time the death purportedly took place. Likewise it is a general fact, assuming that backward causation (or time travel) is physically possible, that we can retro-kill anybody who is not alive after the time the purported death took place. But the explanation of a general fact requires an appeal to a general fact or a law of nature. Thus a reference to a singular contingent fact to explain why you never succeed in killing your younger self seems not to fulfil the requirement of being an explanation.

The problem may be better understood in following way: each time you try to retro-kill somebody who is not alive after the time the purported effect of killing took place, your assassination may still fail because of your hand was shaking, etc. Such particular facts explain why you actually missed the target which you in principle were able to hit. But to say that you are in principle able to perform retro-killing means that there are laws of nature that normally allow you to perform such an action in the appropriate circumstances. Similarly, each time you try to retro-kill somebody who is alive after the purported death took place, you may fail for one reason or another. But you must always fail to retro-kill somebody who is alive after you did your action, i.e., you are in principle unable to retro-kill such a person. In those cases it is physically impossible for you to kill, say, your younger self. It seems, therefore, that there should be some laws of nature, working on either a local level or a global level, which violate such an action and makes it physically impossible.

A possible solution may be found in a recent result which shows that the most basic features of quantum mechanics may ensure that we could never alter the past, even if it should be possible to interact with the past. The two physicists, Daniel Greenberger and Karl Svozil (2005 in Other Internet Resources ), imagine some form of quantum mechanical feedback by introducing figurative beam splitters which are unitary, i.e., the splitters allow the feedback loop to be reversed because they have the same number of entry ports and exit ports. From quantum mechanics we know that an object may behave like a wave and that some unitary operator describes the propagation of a physical system. The system is represented by a wave function, also referred to as a path, and the time evolution of the system is calculated as a sum over all possible paths from the initial state to the final state. This calculation is usually restricted to the forward direction of time. Now, if we think of some of the paths as unfolding backwards in time, Greenberger and Svozil are able to prove that either the forward and the backward component paths of the loop cancel out, or that the propagator, which establishes the feedback in time, “wipes out the alternative possible futures, thus guaranteeing the future that has already happened”. Thus, if you could aim at something in the past, the laws of nature prohibit you to act in ways that are in conflict with what makes the future what it is (what it already turned out to be). The authors’ conclusion is that if you go back in time or effect “the past quantum mechanically, you would only see those alternatives consistent with the world you left behind you”.

This thought experiment involves a player playing a game against a fortune teller. In this game there are two boxes of which the player may select one or both. One of the two boxes is transparent, let’s call it \(A\), the other is opaque, call it \(B\). Before the player makes her choice the fortune teller, based on her prediction of the player’s choice, puts a certain amount of money in one or both boxes. When the player makes her choice, the following information is available to her: 1) Up to now the fortune teller has been able to predict the future with absolute certainty and has foreseen what other players have chosen. Moreover: 2) sometimes the fortune teller puts 1,000,000 dollars in box \(B\), but only if the player selects box \(B\) and does not take both boxes, whereas she puts 1,000 dollars in box \(A\), regardless of whether the player chooses box \(A\) or both boxes. So when the player has to choose between the two boxes, it is already determined whether box \(B\) contains 1,000,000 or nothing. If the fortune teller is correct in her prediction, the player will get 1,000,000 dollars, only if she selects box \(B\); however, if the player wants to earn 1,001,000 dollars and selects both boxes, she will miss most of the fortune and only receive 1,000 dollars, which she can already see in box \(A\).

This puzzle was originally proposed by William Newcomb but never published. After its first publication by Robert Nozick (1969) it was much discussed within decision theory. But it has also been debated in the context of backward causation, because it gives a nice illustration of some of the philosophical problems that arise in relation to backward causation. In this debate it has been used to demonstrate various claims: that backward causation is impossible or that it implies fatalism or determinism. The earliest discussion of some of the consequences for backward causation and free will can be found in George Schlesinger (1974) and in an exchange between Don Locke (1978, 1979) and André Gallois (1979). Here Schlesinger argued that there are good arguments for taking both boxes, \(A\) and \(B\), and equally good arguments for taking only box B, whereas Locke held that backward causation is irrelevant and the player ought to take both boxes. However, Gallois believed that Locke’s arguments for taking both boxes are misconceived.

Two opposite arguments for what the player should decide can be given. Assuming the player has a free will it seems rational to say that the fortune teller cannot in principle predict what the player is going to do. When the player makes her choice, it is already determinate whether box \(B\) contains 1,000,000 dollars or nothing. Therefore her choice cannot be affected by the fortune teller’s prediction, and she would be better off by selecting both boxes, hoping that there already is 1,000,000 dollars in box \(B\). The other argument maintains that based on previous experience—which tells us that the fortune teller has always been correct about her predictions—it would be most rational of the player to take only \(B\). From here philosophers have disagreed about the strength of the argument. One could insist that fortune teller can predict the player’s choice only based on relevant knowledge of that person’s past or present behavior or state of mind (compatibilism). Alternatively one could argue that the fortune teller could have such a perfect knowledge only from information about the player’s choice in the future.

Nevertheless, it has been argued that the Newcomb paradox demonstrates that backward causation is impossible. George Schlesinger (1980:75 ff.), for instance, imagines a perfect judge who is allowed to check the two boxes after the fortune teller has placed the money in the boxes, but before the player has made her choice. It is clear that if the perfect judge then informs the player about the content of the two boxes, we have a case where the fortune teller’s prediction causes the player to select both boxes as she is informed about the 1,000,000 dollars in box \(B\). Indeed this would be a clear example of Black’s case of bilking. But Schlesinger also argues that the same holds true, if the perfect judge merely knows it without informing the player. However, it is difficult to understand why this should be the conclusion. If we assume that the player has a free will and that the fortune teller is able to predict the result of the player’s choice, it seems most rational for the player to learn from experience and opt for box \(B\) only rather than being greedy and take both boxes. As long as the perfect judge is silent, his knowledge about the content of the two boxes seems not to be able to influence the player’s decision. Nor does the player’s possible knowledge of the existence of a perfect judge seem to have any effect on her decision, because this information does not add anything to the information she already has; namely, that the fortune teller has placed the money in the boxes before she makes her decision and that the fortune teller has never failed to predict the outcome in advance.

Another problem is that the paradox seems to indicate that backward causation implies fatalism and determinism. If backward causation is possible we cannot have a free will. If the result of the player’s action can be predicted, because it is already true today what the player will choose tomorrow, she cannot be free to pick. If the fortune teller already knows that the player will choose both boxes, this has to be true, and the player cannot do otherwise. And if the fortune teller already knows that the player will select only box \(B\), this has to be true, and the player cannot but do it. However, this argument seems to be misguided.

The intuitive strength of the argument stems from the general assumption that backward causation presupposes an ontologically closed future—a metaphysical position about time usually named eternalism . Hence it is not an argument only against backward causation but against eternalism as well. Suppose it is now already true or false what is going to happen tomorrow; then there must be some future truth-makers that determine that it is now already true or false what is going to happen. The consequence seems to be that what the player is going to do tomorrow is already determined today; hence the player cannot do otherwise tomorrow than what is true today. Therefore the player cannot have a free choice, and it seems futile of her to make any decision.

However, it can be maintained that the player still has her free choice. Nothing around the fortune teller causes the player to make a particular decision. The player is as free as she would be with no prediction. What the fortune teller is able to predict is the result of the player’s choice. The choice itself may nevertheless be free. Moreover, unless one replaces forward causation with backward causation, one cannot argue that it is the outcome of the player’s choice that causes her decision. The statement about the outcome of her decision is true, according to the fortune teller, because of the particular decision the player makes; a statement about the player’s decision is not true because of the outcome of her decision. Consequently, even with respect to the fortune teller, the player’s decision may be regarded as free in the sense that nothing in its past nor in its future determines what the decision actually becomes. The reason why the fortune teller is able to make her prediction could be that the player’s choice instigates an information channel backwards in time.

Philosophers who reject eternalism may not leave the discussion here. They could argue that it may very well be the case that the player’s choice is neither causally determined by past events nor by future events. Yet, eternalism implies that the player’s decision is ontologically determinate before it is made, since it is true today what she will decide tomorrow. Therefore she is not as free as she would be if the future is ontologically open, i.e., it is not yet ontologically determinate what the future is going to be, including the player’s choice. The eternalist may attempt to rebut these critics by arguing that as long as the player’s decision is not causally determined, it is free in any possible sense.

The notion of backward causation raises a very different set of questions that need to be answered before a physically adequate notion has been developed.

What, if anything, would in physical terms characterize backward causation?

One has to remember that causality as such is an everyday notion that has no natural application in physics. How we could physically identify backward causal processes depends very much on which feature we take our ordinary notion of causation to apply to a physical process. In physics we may be tempted to associate it with different physical notions of processes. Four suggestions have been put forward: (a) the causal link can be identified with the transference of energy; (b) it can be identified with the conservation of physical quantities like charge, linear and angular momentum; (c) it can be identified with interaction of forces; or (d) it can be identified with the microscopic notion of interaction. It appears with respect to all four suggestions, however, that the involved descriptions are invariant under the time reversal operation.

The most fundamental laws of nature are time reversal invariant in the sense that our physical theories allow description of the fundamental reactions and processes in terms of the time reversed order. Such processes are said to be reversible in time. Maxwell’s theory of electromagnetism, for instance, admits two kinds of mathematical solutions for the equations describing the radiation of energy in an electromagnetic field. One is called the retarded solution where radiation appears as outgoing concentric waves, the other is named the advanced solution according to which radiation appears as incoming concentric waves. Apparently the advanced solution describes the temporal inverse phenomena of the retarded solution so that these two solutions are usually regarded as the time reverse solution of the other. Nevertheless, retarded waves, like the increase of entropy in quasi-closed systems, appear to be de facto irreversible although they are described in terms of time invariant laws. Nature seems to prefer certain processes rather than their temporally inversed counterparts in spite of the fact that the laws of nature do not show such a preference. Light, radiation and ripples on a pond always spread outwards from their source rather than inwards just like entropy of a quasi-closed system is always moving from lower to higher states.

Why do we not see any advanced waves in nature? Wheeler and Feynman (1945) came up with an answer. If we assume, they said, that radiation from an isolated accelerated charged particle is equally retarded and advanced, that is half retarded and half advanced to be exact, we can explain why it appears to be fully retarded in terms of the influence distant absorbers make on the source. The absorber consists of charged material that reacts with the source field by radiating with half retarded and half advanced waves. It is this half advanced field of the charged particles of the absorber which is added to the half retarded field of the source. The advanced waves of the absorber interfere constructively with the retarded waves of the source, whereas the same waves cancel out the advanced waves of the source in a destructive interference. Thus one of the consequences of Wheeler and Feynman Absorber Theory is the idea that emitters are intrinsically symmetric, another is that there is no intrinsic difference between so-called emitters and so-called absorbers. In other words, if this theory is true we have to conclude that radiation from a source is a time symmetric process but the presence of an absorber makes it asymmetric.

The Wheeler-Feynman theory takes for granted that outgoing, expanding waves are identical with retarded radiation and incoming, contracting waves with advanced radiation. But is such identification without any problems? Not quite. An example with retarded and advanced emitters illustrates clearly why. Think of a stone being thrown directly into the middle of a circular pond. The ripples move outwards from the point where the stone hits the water (the source) in a coherent, organized wave front and eventually reach the edges (the absorber). Moreover, the source acts earlier than the absorber. What will the inverse process look like? It depends on how we understand such a process, whether or not we consider a case that includes a reversed source and a reversed absorber. (A) If they are included, the edges of the pond will now act as the source and the converging waves will eventually reach the middle of the pond. We may create something like this if we dropped a big ring horizontally into the pond. Inside the ring the waves would move inwards in an organized wave front towards the centre. In this case the source (the drop of the ring) would still act earlier than the absorber (the ripples meeting at the middle of the pond from all sides). (B) But if our understanding of the inverse process does not include an exchange of the source with the absorber and vice versa , then the ripples reach the edges of the pond (the absorber) earlier than the stone plunges into the water (the source). This is definitely not a state of affairs we could bring about. Furthermore, if we were to observe such a process, the ripples would seem to move inwards as contracting waves. The problem is that both kinds of inverse processes would seem to appear to us as organized incoming waves but one would be a case of retarded radiation and the other of advanced radiation.

This may not be the only problematic assumption of the Wheeler and Feynman theory. Huw Price (1996) has singled out other problems. Among them is the question of how we may experience the difference between retarded and advanced waves. When Wheeler and Feynman attributed to the source a field of half retarded and half advanced waves, they assumed that the field actually consists of retarded as well as an advanced component. Price objects, however, that there is no measurable difference between the two kinds of waves, and we cannot justify such a distinction by an appeal to the nature of the source because both emitters and absorbers can be associated with retarded as well as advanced waves. Instead he believes that these components are fictitious and that Wheeler and Feynman’s formalism merely offer two different descriptions of the same wave. The problem of the asymmetry, as he sees it, has nothing to do with the fact that transmitters are associated with outgoing radiation rather than incoming radiation but that transmitters are centered on organized outgoing wave fronts whereas receivers are not centered on similar organized incoming wave fronts.

When the discussion of tachyons began to appear in physics in the 1960s, it was soon noticed that such particles according to some frames of reference were associated with negative energies going backwards in time. To understand how, consider the trajectory of the same tachyon in relation of three different reference frames, \(S, S^*\), and \(S^{**}\) in the Minkowski-space. Now assume that \(A\) is, in relation to \(S\), the emission of a tachyon at \(t_{1}\) and \(B\) is the absorption of the tachyon at \(t_{2}\). According to an observer in \(S, A\) will be earlier than \(B\) and the tachyon will carry positive energy forward in time. Nevertheless it is always possible to select a reference frame \(S^*\) in relation to which an observer will see \(A\) happen simultaneously with \(B\) and yet another reference frame \(S^{**}\) in relation to which an observer sees \(A\) happens at \(t_{2}^{**}\) whereas \(B\) happens at \(t_{1}^{**}\). According to the observer in \(S^{*}\), \(A\) will take place later than \(B\) and the tachyon carries negative energy backwards in time (See Figure 1).

Figure 1: Spacetime diagram of tachyon

In Figure 1 the planes represent the hypersurfaces of simultaneity. In relation to frame \(S\) the tachyon source is at rest, and a tachyon is emitted at event \(A\), with a superluminal but finite velocity. The absorption of the tachyon, event \(B\), will accordingly occur later than \(A\) in relation to the observer in \(S\), and the arrow of trajectory is for that reason pointing into the future above the hypersurface passing through \(A\) and standing perpendicular to the world-line of the source. But neither with respect to the frame \(S^*\) nor \(S^{**}\) is the tachyon source at rest and the hypersurfaces are therefore tilted in relation to the arrow of trajectory. An observer in \(S^*\) observes the tachyon to have infinite speed, and therefore the hypersurface is tilted so much that it coincides with the arrow. The observer in \(S^{**}\) is moving so fast with respect to the tachyon source that the hypersurface becomes titled so much that the arrow points into the past below the hypersurface.

E. Recami (1978) tried to avoid the idea that tachyons could move backwards in time by introducing the so-called reinterpretation principle according to which all negative energy tachyons should be interpreted as if they have positive energy and move forward in time. This would mean that the causal order of tachyons should not be regarded objective since both \(A\) and \(B\) sometimes denoted the emission and sometimes the absorption depending on the frame of reference. There are, however, good reasons to believe that this suggestion does not solve the problems it was intended to (Faye 1981/1989).

Other physical candidates for backward causation can be founded in the physics literature. Richard Feynman once came up with the idea that the electron could go backwards in time as a possible interpretation of the positron (Feynman 1949). In fact he imagined the possibility that perhaps there were only one electron in the world zig-zagging back and forth in time. An electron moving backwards in time would carry negative energy whereas it would with respect to our ordinary time sense have positive charge and positive energy. But few consider this as a viable interpretation today (Earman 1967a, 1976).

More recently, the Bell type experiments have been interpreted by some as if quantum events could be connected in such a way that the past light cone might be accessible under non-local interaction; not only in the sense of action at a distance but as backward causation. One of the most enticing experiments of this kind is the Delayed Choice Quantum Eraser designed by Yoon-Ho Kim et al. (2000). It is a rather complicated construction. It is set up to measure correlated pairs of photons, which are in an entangled state, so that one of the two photons is detected 8 nanoseconds before its partner. The results of the experiment are quite amazing. They seem to indicate that the behavior of the photons detected these 8 nanoseconds before their partners is determined by how the partners will be detected. Indeed it might be tempting to interpret these results as an example of the future causing the past. The result is, however, in accordance with the predictions of quantum mechanics.

However, David Ellerman (2015) argues that interpreting delayed-choice experiments or similar experiments as revealing cases of backward causation or retrocausation relies on what he calls the separation fallacy:

We have seen the same fallacy of interpretation in two-slit experiments, which-way interferometer experiments, polarization analyzers, and Stern-Gerlach experiments. The common element in all the cases is that there is some separation apparatus that puts a particle into a certain superposition of spatially “entangled” or correlated eigenstates in such a manner that when an appropriately spatially-positioned detector induces a collapse to an eigenstate, then the detector will only register one of the eigenstates. The separation fallacy is that this is misinterpreted as showing that the particle was already in that eigenstate in that position as a result of the previous “separation.” In fact the superposition evolves until some distinction is made that constitutes a measurement, and only then is the state reduced to an eigenstate. The quantum erasers are more elaborate versions of these simpler experiments, and a similar separation fallacy arises in that context.

Thus, Ellerman argues that when one describes a system in a superposition of certain eigenstates, it does not mean that the system is in any of these eigenstates before some measurement is carried out. Therefore, it is wrong to interpret delayed-choice experiments, and their like, as if the future measurement determines some past eigenstates, which all were parts of a superposition.

In his discussion of the experimental violation of Bell’s inequalities Don Howard (1989) distinguishes, based on an earlier work done by Jon Jarrett, between locality and separability. The locality condition states that a measurement of a pair of objects emerging from a singlet is statistically independent of the setting of the apparatus used to measure its counterpart. However, the separability condition is defined as the joint probability is equal to the product of the probability of each state. We know that the experimental violation of Bell’s inequalities involves the invalidation of one of these conditions. Moreover, if we take Ellerman’s argument into consideration, the two entangled particles, although separated, are still in a state of superposition until the measurement takes place.

If we consider the notion of the entangled state in quantum mechanics, we find that it is characterized as a unified, non-separable state due to the help of the notion of superposition of possible eigenstates represented by one common wave function for the correlated pair. Such a superposition is neither distance-dependent nor time-dependent. Therefore it is not surprising that based on the correct predictions of quantum mechanics it is impossible to find support of the violation of normal causation within this kind of experiment. With reference to the philosophical discussion about quantum mechanical entanglement, we can conclude that the experimental results of this sort violate the principle of separability rather than the principle of locality.

Phillippe Eberhard and Ronald R. Roos (1989) have established a theorem which says that if quantum mechanics is correct, it is impossible to use quantum effects to generate a break in the chain of normal causation. Quantum field theory does not allow any superluminal communication between different observers. Indeed, this is not so strange, since quantum field theory is relativistically invariant whereas superluminal frames of reference are not. But Eberhard and Roos’ theorem does not rule out all forms of backward causation. Two possible scenarios are still open: (1) entangled pairs exchange some form of superluminal information (and energy) below the limits of Heisenberg’s uncertainty relations; or (2) causation may be symmetrical so that the direction of causation in a physical system is determined by its boundary conditions.

Costa de Beauregard (1977, 1979), for instance, has suggested that when a system of two photons in a singlet state is measured by two observers in two regions separated by a space-like distance, then it is precisely the act of observation that produces the past of the measuring process in the sense that it influences the source that emitted the two photons. de Beauregard’s idea is that the element of reality being revealed in the formulation of the EPR paradox is real only because it was created by actually performed acts of observation that was propagated backwards in time with one of the two correlated quantum objects from the measuring device to the source of the photons.

Some physicists, like Elitzur et al. (2016), suggest a form of too-late-choice experiment that supports such a time-symmetric interpretations of quantum mechanics according to which backwards causation plays a significant role. In the normal EPR experiment, each measurement determines, say, the spin value of two separated, say, electrons in a singlet state along a certain orientation of the apparatus. The outcome then proves that the spin value of one electron has been affected by the distant experimenter’s choice of spin orientation of the other electron. However, what Elitzur et al. now imagine is a reversal setting in which a chosen spin value determines the corresponding orientation. Based on their analysis, they conclude that “it turns out that the orientation is similarly subject to nonlocal effects [as the spin value.]”

Several other philosophers and physicists have come forward with similar ideas. Aharonov and Vaidman (1997) have formulated a two vector approach to quantum mechanics “in which a quantum system is described, at a given time, by two (instead of one) quantum states: the usual one evolving toward the future and the second evolving backwards in time from a future measurement.” Also Cramer’s transactional interpretation of quantum mechanics involves the idea of a second wave travelling backwards in time (Cramer, 1986). The basic assumption behind all of them is that in the micro-world we find only causal symmetry, and this fact together with proper boundary conditions can be used to give an explanation of outcomes that seem otherwise paradoxical. Such quantum correlation experiments can, however, be interpreted in many other ways. In the end it seems as if it all depends one whether one assumes that Bell experiments break with either the locality condition or the separability condition. A time-symmetric interpretation of quantum mechanics is required only if one believes that it is the locality condition that is violated in order to avoid being in conflict with relativity theory.

These alleged examples of backward causation have one thing in common. They are all based on the idea that fundamental physical processes are by themselves symmetric in nature. Our ordinary notion of causation does not track any nomological feature of the world. What counts as the cause and the effect depends on the observer’s projection of his or her temporal sense onto the world. So it is still an open question how a coherent notion of backward causation can fit into this general understanding of nature. The question we therefore have to answer is the following:

How can we distinguish between forward causation and backward causation if all basic physical processes are time symmetric according to our description of nature?

Two very different reactions to this problem seem possible.

4.4.1 Boundary Conditions

One proposal is to say that if we came across reversed cases of de facto irreversible processes, such as running a film backwards in which the cream converged in a coffee cup, such cases should be interpreted as examples of backward causation (Price 1996). Such a claim build on a common interpretation of time reversal invariance of processes according to which this descriptive feature of the dynamical equations of physics makes reversal processes symmetric in time. Many philosophers have defended such an interpretation, in particular Hans Reichenbach (1956, 1929 [1958]) and Adolf Grünbaum (1963). This also led them to argued that only de facto irreversible processes, such as those described by statistical thermodynamics, could be used to defined a physical orientation of time. Thus, it seems to be the case that the actual world consisting of mostly de facto irreversible processes on the macroscopic level due to a prevalent set of boundary conditions is temporally and causally symmetric on the microscopic level. On the macroscopic level, de facto irreversible processes emerge, because the boundary conditions are a result of the huge degree of freedom among microprocesses or coherence conditions forced upon the underlying microscopic processes.

The point is here to argue that it is the absence of the right initial or boundary conditions on the macroscopic level that makes backward causation so rare or nearly empirically impossible. This suggestion is based on three basic assumptions: (i) there is no objective asymmetry in the world, causal processes are intrinsically symmetric in nature, or causation is bidirectional, and therefore the fundamental processes of the micro-world are temporally symmetric; (ii) causal asymmetry is subjective in the sense that any attribution of an asymmetry between cause and effect depends on our use of counterfactuals and our own temporal orientation; (iii) backward causation, or advanced action, is nonetheless possible because sometimes the correlation of certain past events depends on the existence of causally symmetric processes and some future boundary conditions. For instance, advanced actions in electrodynamics require that the existence of transmitters in the future are centered on organized incoming wave fronts; and advanced actions in quantum mechanics require that their present states are in part determined by the future conditions (measurements) they are to encounter. This feature is then taken to explain quantum entanglement and the violation of Bell’s inequalities in quantum mechanics.

A simple consideration seems to support this interpretation. Think of a particle travelling between two boxes. The normal observer and the counter-observer who has an inverse time sense will describe the exchange in conflicting terms. To the normal observer Box 1, say, will be considered as the emitter because it loses energy before anything in Box 2 happens. Therefore, Box 2 will be considered as the receiver since it gains energy at a later time. So in relation to the normal observer, the particle travels from Box 1 to Box 2. The counter-observer, however, sees the situation with opposite eyes. In relation to him, Box 2 loses energy and not until thereafter does Box 1 gain a similar amount of energy. Accordingly, in relation to the counter-observer, the particle moves from Box 2 to Box 1. In other words whether a box is considered to be an emitter or a receiver depends on the observer’s time sense.

4.4.2 Nomic conditions

The other proposal denies that basic physical processes are time symmetric and argues, in contrast, that the causal asymmetry is objective and therefore that there exists an intrinsic difference between the cause and the effect of all physical processes. John Earman (1967b and 1969) may be the first who argued against the interpretation that time reversal invariance of processes is identical with invariance under the exchange of the temporal order between earlier and later . Two reversed tokens of the same type of physical process do not developed in the opposite direction of time.

Hence, backward causation should not be considered as a notion about boundary conditions but as a notion concerned with processes that nomically distinguish themselves from forward causal processes. Thus, if there are processes in the world that might be seen as a manifestation of backward causation, these are not to be depicted by a description that leaves them to be time reversed cases of ordinary forward causal processes (Faye 1981/1989, 1997, 2002). This alternative interpretation rests on a basic claim and four assumptions.

The fundamental claim is that for any observer it is possible to identify experimentally the cause and the effect so that these remain the same even in relation to counter-observers, i.e., observers having the opposite time sense of ours. In support of this claim consider the following thought experiment. Two boxes, each having a shutter, are facing each other. Assume, ex hypothesis, that Box 1 is the particle source and Box 2 is the particle receiver. The question is how a normal observer and a counter-observer can come to agreement that particles move from Box 1 to Box 2. The answer can be found through a series of manipulations with the shutters, I would say. There are four possible combinations of the two shutters: open-open, close-close, open-close, close-open. Let us call any change of energy in Box 1, regardless of whether it emits or receives a particle, \(A\) and, similarly, any change of energy in Box \(2 B\). Whether \(A\) or \(B\) stand for a gain or a loss of energy can be determined by weighing the two boxes. (i) In case both boxes are closed, no particle will leave Box 1 and no particle is received by Box 2, thus no gain or loss of energy occurs, and both the normal observer and the counter-observer see a situation of not-\(A\), not-\(B\). (ii) In case both boxes are open a particle leaves Box 1 and is received by Box 2. Again this can be observed by measuring the change of energy in the two boxes. Thus the observers will see a situation of both \(A\) and \(B\). (iii) In case Box 1 is closed and Box 2 is open, they will observe no change of energy in Box 1 (because it is closed) and, since no particle is leaving Box 1, no particle will reach Box 2 although its shutter is open. Hence the observers measure no energy change in this box. Thus they see not-\(A\) and not-\(B\). (iv) Finally, if Box 1 is open and Box 2 is closed, a particle leaves Box 1, but none is received by Box 2. In other words, there is a loss or a gain of energy in Box 1, but no loss or gain of energy in Box 2. So the observers see \(A\) and not-\(B\). The upshot of this toy experiment is that the normal observer as well as the counter-observer experience two \(A\)s but only one \(B\), and one not-\(A\) but two not-\(B\)s; therefore both will agree that the particles move from Box 1 to Box 2.

This means that what a normal observer identifies as a forward causal process will be regarded as a backward causal process in relation to the counter-observer in the sense that the very same event acting as a past cause for the normal observer will act as a future cause for the counter-observer. This indicates, too, that in relation to a normal observer forward causation and backward causation cannot be regarded as two different manifestations of nomologically reversible (but de facto irreversible) processes since both manifestations—the common process and the very improbable reversed process—would develop forward in time. If this claim is true, it implies that the description of physical processes should reflect such an intrinsic asymmetry in a way that the nomic description varies according to whether the process in question goes forward or backwards in time. Moreover, we must also be able to distinguish theoretically (and not only experimentally) between the normal observer’s report and the counter-observer’s report of the same process by a separate convention in respect to whether the process is forward moving or backward moving. What we want is a characterization of every physical process so that the invariance of cause and effect corresponds to nomological irreversibility.

In order to establish a nomic, intrinsic distinction between forward causal processes and backward causal processes one has to take departure in four assumptions. (i) Process tokens and process types are distinct in the sense that only process types are reversible, process tokens are not. (ii) A normal observer will describe causal processes propagating forward in time in terms of positive mass and positive energy states pointing into her future whereas she will describe the same tokens in terms of negative mass and energy states pointing into her past . This reflects two possible solutions of the four-momentum vector in the theory of relativity. (iii)Thus, one must distinguish between a passive time reversal operation and an active time reversal operation. The passive transformation is applied to the same process token by describing it in terms of opposite coordinates and opposite energy states. The active transformation, in contrast, brings about another token of the same process type in virtue of some physical translation or rotation of the system itself, both tokens having the same energy sign pointing in the same direction of time. (iv) The description in terms of positive mass and the positive energy flow corresponds to the intrinsic order of the propagation.

Now, let us try to apply the nomic interpretation to the above consideration concerning the exchange of a particle between two boxes. In relation to the normal observer who describes the particle in terms of its positive energy component , it travels from Box 1 to Box 2 because Box 1 looses energy at an earlier time and Box 2 gains energy at a later time. The same situation is by the counter-observer described in terms of the particle’s negative energy component as a situation where something happens in Box 2 before it happens in Box 1. In relation to the counter-observer, Box 2 would not, as the boundary interpretation suggests, loose energy. On the contrary, Box 2 would seem to gain energy, but the counter-observer would describe the particle as a series of negative energy states reaching into his future supposing the particle to be moving from Box 2 to Box 1 carrying negative energy. But, as we have just argued, the particle really moves from Box 1 to Box 2, from the counter-observer’s future into his past carrying positive energy.

Consequently, the nomic interpretation holds that in relation to our normal time sense the causal direction of ordinary processes is identical with that of their reversed processes. In other words, take two tokens of a nomologically reversible process type, say \(A\) and \(B\), and let \(B\) be the actively time reversed process of \(A\), then this interpretation claims that \(A\) and \(B\) causally develop in the same direction of time. So, according to this view, neither incoming, contracting electromagnetic waves nor the decrease of entropy would count as examples of backward causation as long as such processes involve ordinary types of matter, i.e., matter that possesses positive mass and/or energy pointing, in relation to our normal time sense, towards the future. The notion of backward causation should instead be applied to matter of a different type, particles that appear to have, according to usual conventions, negative mass and/or energy pointing, in relation to our normal time sense, towards the future but positive mass and/or energy pointing towards the past . Such advanced matter, if it exists, should be distinguished from both ordinary retarded matter as well as tachyons by always being described with respect to our time sense in terms of negative mass and energy stretching forward in time. A consequence is that a world in which advanced matter exists together with retarded matter, and where advanced matter is able to interact directly with the same amount of retarded matter, both would, in case they actually did interact, annihilate without leaving any trace of energy.

How and whether the notion of backward causation has a role to play in physics has yet to be seen. But as long as no common agreement exists among philosophers and physicists about what in the physical description of the world corresponds to our everyday notion of causation, it would still be a matter of theoretical dispute what counts as empirical examples of backward causation.

Aharonov, Y. and L. Vaidman, 1997, “Protective measurements of two-state vectors”, in Cohen, R.S., Horne, M., & Stachel, J. (eds.), Potentiality, Entanglement and Passion-at-a-Distance: Quantum Mechanical Studies for Abner Shimony , (Volume 2), Dordrecht: Springer, pp. 1–8.
Arons, M.E. and E.C.G. Sudarshan, 1968, “Lorentz Invariance, Local Field Theory and Faster-than-Light Particles”, Physical Review , 173(5): 1622–1628.
Baker, S., 2003, “Counterfactual Analyses of Causation: The Problems of Effects and Epiphenomena Revisited”, Noûs , 37(1): 133–150.
Bennett, J., 1974, “Counterfactuals and Possible Worlds”, Canadian Journal of Philosophy , 4: 381–402.
Bilaniuk, O.M.P, V.K. Deshpande, and E.C.G. Sudarshan, 1962, “’Meta’ Relativity”, American Journal of Physics , 30(2): 718–723.
Bilaniuk, O.M.P. et al. , 1969, “More About Tachyons”, Physics Today , 22(12): 47–51.
Bilaniuk, O.M.P. and E.C.G. Sudarshan, 1969, “Particles beyond the light barrier”, Physics Today , 22(5): 43–51.
Black, M., 1956, “Why Cannot an Effect Precede its Cause”, Analysis , 16: 49–58.
Choi, S., 2007, “Causation and Counterfactual Dependence”, Erkenntnis , 76(1): 1–16.
Cramer, J., 1986, “The transactional interpretation of quantum mechanics”. Review of Modern Physics , 58(July), 647–688.
Csonka, P.L., 1970, “Causality and Faster than Light Particles”, Nuclear Physics , B21: 436–444.
Curry, R., 2015, “Retrocausal Models of EPR”, Studies in History and Philosophy of Science. Part B: Studies in History and Philosophy of Modern Physics. , 49: 1–9.
de Beauregard, C., 1977, “Time Symmetry and the Einstein Paradox”, Il Nuovo Cimento , 42B: 41–64.
–––, 1979, “Time Symmetry and the Einstein Paradox–II”, Il Nuovo Cimento , 51B: 267–279.
Dorato, M., 1995, Time and Reality: Space-Time Physics and the Objectivity of Temporal Becoming , Bologna: CLUEB.
Dummett, M., 1954, “Can an Effect Precede its Cause”, Proceedings of the Aristotelian Society , 28(Supplement): 27–44.
–––, 1964, “Bringing about the Past”, Philosophical Review , 73: 338–359.
Earman, J., 1967a, “On going Backward in Time”, Philosophy of Science , 34: 211–222.
–––, 1967b, “Irreversibility and Temporal Asymmetry”, The Journal of Philosophy , 47: 543–549.
–––, 1969, “The Anisotropy of Time”, Australasian Journal of Philosophy , 47: 273–295.
–––, 1976, “Causation: A Matter of Life and Death”, The Journal of Philosophy , 73: 5–25.
Eberhard, P.H. and R.R. Ross, 1989, “Quantum Field Theory cannot provide Faster-than-Light-Communication”, The Foundation of Physical Letters , 2: 127–149.
Elitzur, A.C., E. Cohen, and T. Shushi, 2016, “The too-late-choice experiment: Bell’s proof within a setting where the nonlocal effect’s target is an earlier event”, International Journal of Quantum Foundation 2: 32–46.
Ellerman, D., 2015, “Why delayed choice experiments do Not imply retrocausality”, Quantum Studies: Mathematics and Foundations , 2: 183–199.
Evans, P.W., 2015, “Retrocausality at no cost”, Synthese , 192: 1139–1155.
Faye, J., 1981/1989, The reality of the future , Odense: Odense University Press.
–––, 1994, “Causal Beliefs and their Justification”, in J. Faye, U. Scheffler & M. Urchs (eds.), Logic and Causal Reasoning , Berlin: Akademie Verlag, pp. 141–168.
–––, 1997, “Causation, Reversibility, and the Direction of Time”, in J. Faye, U. Scheffler & M. Urchs (eds.), Perspectives on Time (Boston Studies in the Philosophy of Science: Volume 189), Dordrecht: Kluwer, pp. 237–266.
–––, 2002, “When Time Gets Off Track”, in C. Callender (ed.) Time, Reality, and Experience , Cambridge: Cambridge University Press.
Feinberg, G., 1967) “Possibility of Faster-Than-Light Particles”, Physical Review , 159(5): 1089–1105.
Feynman, R.P., 1949, “The Theory of Positrons”, Physical Review , 76: 749–459.
Flew, A., 1954, “Can an Effect Precede its Cause”, Proceedings of the Aristotelian Society , 28(Supplement): 45–62.
–––, 1956, “Effects before their Causes—Addenda and Corrigenda”, Analysis , 16: 104–10.
–––, 1956–7, “Causal Disorder Again”, Analysis , 17: 81–86.
Gale, R., 1965, “Why a Cause Cannot be Later than its Effects”, Review of Metaphysics , 19: 209–234.
Gallios, A., 1979, “How not to make a Newcomb Choice”, Analysis , 39(1): 49–53.
Garrett, B., 2020, “Max Black and Backwards Causation”, Argumenta , 1–5. doi:10.14275/2465-2334/20200.gar
Gorovitz, G., 1964, “Leaving the Past Alone”, Philosophical Review , 73: 360–371.
Grünbaum, A., 1963, Philosophical Problems of Space and Time , New York: A.A. Knopf; 2nd expanded edition, 1973, published in Boston Studies in Philosophy of Science .
–––, 1967, Modern Science and Zeno’s Paradoxes , Middletown: Wesleyan University Press.
Gärdenfors, P., 2006, How Homo Became Sapiens , Oxford: Oxford University Press.
Horwich, P., 1987, Asymmetries in Time , Cambridge, MA: MIT Press.
–––, 1993, “Lewis’s programme”, in E. Sosa & M. Tooley (eds.), Causation , New York: Oxford University Press, pp. 208–216.
Howard, D., 1989, “Holism, Separability, and the Metaphysical Implication of Bell Experiments”, in J. Cushing and E. McMullin (eds.), Philosophical Consequences of Quantum Theory: Reflections on Bell’s Theorem , Notre Dame: The University of Notre Dame Press.
Hume, D., 1748 [2007], An Enquiry concerning Human Understanding , edited with an introduction and notes by Peter Millican, Oxford: Oxford University Press.
Kim, Y-H. et al. , 2000, “A Delayed Choice Quantum Eraser”, Physical Review Letters , 84: 1–5.
Lewis, D.K., 1973, “Causation”, Journal of Philosophy , 70: 556–567.
–––, 1976, “The Paradoxes of Time Travel”, American Philosophical Quarterly , 13: 145–152.
–––, 2000, “Causation as Influence”, Journal of Philosophy , 97: 182–197.
Locke, D., 1978, “How to make a Newcomb Choice”, Analysis , 38(1): 17–23.
–––, 1979, “Causation, Compatibilism and Newcomb’s Problem”, Analysis , 39(4): 210–211.
Maudlin, J., 2002, Quantum Non-locality and Relativity , Oxford: Blackwell Publishing.
Mellor, D.H., 1981, Real Time , Cambridge: Cambridge University Press.
–––, 1991, “Causation and the Direction of Time”, Erkenntnis , 35: 191–203.
Nozick, R., 1969, “Newcomb’s Problem and Two Principles of Choice”, in R. Rescher et al. (eds.) Essays in Honor of Carl. F. Hempel , Dordrecht: Reidel, pp. 114–146.
Price, H., 1996, Time’s Arrow and Archimedes’ Point , Oxford: Oxford University Press.
–––, 2012, “Does time-symmetry imply retrocausality? How the quantum world says ‘Maybe’?”, Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics , 43 (2): 75–83.
Recami, E., 1978, “How to Recover Causality in Special Relativity for Tachyons”, Foundations of Physics , 8: 329–340.
Reichenbach, H., 1956, The Direction of Time , Berkeley: University of California Press.
–––, 1928 [1958], The Philosophy of Space and Time , New York: Dover, 1958, translated by Maria Reichenbach and John Freund, from his 1928 Philosophie der Raum-Zeit-Lehre .
Schlesinger, G., 1974, “The Unpredictability of Free Choices”, British Journal for the Philosophy of Science , 25(3): 209–221.
–––, 1980, Aspects of Time , Indianapolis: Hackett.
Seli, G., 2020, “A Troublesome Case of Backward Causation for Lewis’s Counterfactual Theory”, Analytic Philosophy , 1–20. doi:10.1111/phib.12186
Tanaka, S., 1960, “Theory of Matter with Super Light Velocity”, Progress of Theoretical Physics , 24(1): 171–200.
Wasserman, R., 2015, “Lewis on Backward Causation”, Thought , 4: 141–151.
Wharton, K., 2018, “A New Class of Retrocausal Models”, Entropy , 20(6): 410; doi:10.3390/e20000410
Wheeler, J.A. and R.P. Feynman, 1945, “Interaction with the Absorber as the Mechanism of Radiation”, Reviews of Modern Physics , 17: 157–181.
Woodward, J., 2003, Making Things Happen: A Theory of Causal Explanation , New York: Oxford University Press.

How to cite this entry . Preview the PDF version of this entry at the Friends of the SEP Society . Look up topics and thinkers related to this entry at the Internet Philosophy Ontology Project (InPhO). Enhanced bibliography for this entry at PhilPapers , with links to its database.

Greenberger, D.M. & Svozil, K., 2005, “ Quantum Theory Looks at Time Travel ”, preprint at arXiv.org. This paper contains minor changes to the Greenberger and Svozil paper published as Chapter 4 of Quo Vadis Quantum Mechanics? , ed. by A. Elitzur, S. Dolev and N. Kolenda, Berlin: Springer Verlag, 2005. It is an expanded version of D.M. Greenberger and K. Svozil, in Between Chance and Choice , ed. by H. Atmanspacher and R. Bishop, Thorverton England: Imprint Academic, 2002, pp. 293–308.

space and time: being and becoming in modern physics | time | time travel | time travel: and modern physics

Acknowledgments

Thanks to John Norton for his editorial suggestions and for his drawing of Figure 1.

Accessibility

Support SEP

Mirror sites.

View this site from another server:

Info about mirror sites

Library of Congress Catalog Data: ISSN 1095-5054

Retrocausality Is the Key to Time Travel. What the Hell Is Retrocausality?

Cause always leads to effect — except, of course, in particle physics.

Since you first started learning about the world, you’ve known that cause leads to effect. Everything that’s ever happened to or near you has reiterated this point, making it seem like a fundamental law of nature. It isn’t.

It is, in fact, possible for an event to occur before its causal factors have manifested or happened. This isn’t how appliances work — you don’t have to worry about will have having left the oven on — but it is how particle physics works. It’s also the key to explaining how time travel, under the laws of quantum physics, could operate.

Retrocausality, or reverse causality, is the idea that an effect can happen before its cause. It’s often used as a thought experiment by scientists considering the philosophical underpinnings of physics, and whether the future can affect the present the same way the present affects the future.

There are a lot of time-independent parts of quantum mechanics that leave open the possibility that particles or information — like the hypothetical tachyon particle that always moves faster than light — can travel back in time.

Retrocausality is used to explain several different strange physics phenomena. The most arguably famous has to do with the Wheeler-Feynman absorber theory, developed by the renowned John Archibald Wheeler and Richard Feynman. It’s a bit complicated, so the quick-and-dirty version is that the theory explains how a special type of wave (or lack thereof) in a certain quantum equation would work so that you don’t have an instance where a charged particle has to act on itself (which would, in normal circumstances, lead to an infinitely-driving self-force).

Scientists thinking about how retrocausality can explain particle time travel specifically avoid logical contradictions like the grandfather paradox (where a future effect negates its cause and results in a dead grandfather and genetically disconnected grandchild). So we don’t have to get into a lot of sticky situations where things don’t add up.

The theory instead proposes that a positron is an electron moving backward in time so that they have a positive charge. If this is true, it explains positron-electron annihilation not as an act of creation and destruction, but actually as a simple change in direction of moving particles through a single dimension — in this case, the dimension of time . The annihilation of both particles is, in essence, an event that happens prior to the cause (the electron moving backward).

Time travel, therefore, would essentially be an object’s particles moving in reverse direction such that it takes on an opposite charge.

Retrocausality has also been suggested as being possible in extreme spacetime situations, like traversable wormholes. Closed timelike curves could create reverse causal situations where something that’s observed in the present is the result of exotic matter behaving a certain way in the future. So if wormholes might indeed play a role in helping future humans move through vast distances of spacetime , it could very well be because of events that haven’t even happened yet.

None of this can actually explain the practical things that happen in our everyday lives. If you act like an asshole and you start blaming it on future events, you’re not being clever — you’re just being more of an asshole. Show an actual instance of time travel via reverse moving particles, and you’ll have a good excuse for getting away with being an asshole.

Search Menu
Sign in through your institution
Advance articles
Author Guidelines
Open Access
Why Publish with PQ?
About The Philosophical Quarterly
About the Scots Philosophical Association
About the University of St. Andrews
Editorial Board
Advertising and Corporate Services
Journals Career Network
Self-Archiving Policy
Dispatch Dates
Journals on Oxford Academic
Books on Oxford Academic

Article Contents

I INTRODUCTION
II WHY THINK OTHERWISE?
III THE ONE‐PARTICLE ARGUMENT
IV THE MANY‐PARTICLE ARGUMENT
V AN EASY ARGUMENT?
< Previous

Time Travel Without Causal Loops

Article contents
Figures & tables
Supplementary Data

Bradley Monton, Time Travel Without Causal Loops, The Philosophical Quarterly , Volume 59, Issue 234, January 2009, Pages 54–67, https://doi.org/10.1111/j.1467-9213.2008.564.x

Permissions Icon Permissions

It has sometimes been suggested that backwards time travel always incurs causal loops. I show that this is mistaken, by describing worlds where backwards time travel occurs and yet no causal loops occur. Arguments that backwards time travel can occur without causal loops have been given before in the literature, but I show that those arguments are unconvincing.

Email alerts

Citing articles via.

Contact the University of St. Andrews
Contact the Scots Philosophical Association
Recommend to your Library

Affiliations

Online ISSN 1467-9213
Print ISSN 0031-8094
About Oxford Academic
Publish journals with us
University press partners
What we publish
New features
Open access
Institutional account management
Rights and permissions
Get help with access
Accessibility
Advertising
Media enquiries
Oxford University Press
Oxford Languages
University of Oxford

Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide

Cookie settings
Cookie policy
Privacy policy
Legal notice

This Feature Is Available To Subscribers Only

This PDF is available to Subscribers Only

For full access to this pdf, sign in to an existing account, or purchase an annual subscription.

Subscriber Services
For Authors
Publications
Archaeology
Art & Architecture
Bilingual dictionaries
Classical studies
Encyclopedias
English Dictionaries and Thesauri
Language reference
Linguistics
Media studies
Medicine and health
Names studies
Performing arts
Science and technology
Social sciences
Society and culture
Overview Pages
Subject Reference
English Dictionaries
Bilingual Dictionaries

Simon Blackburn

Find at OUP.com
Google Preview
Share This Facebook LinkedIn Twitter

causal nexus (Latin, nectere , to bind)

The bonding or link between a cause and its effect. The ancient *sceptics, subsequent *occasionalists, and, most famously, ... ...

Access to the complete content on Oxford Reference requires a subscription or purchase. Public users are able to search the site and view the abstracts and keywords for each book and chapter without a subscription.

Please subscribe or login to access full text content.

If you have purchased a print title that contains an access token, please see the token for information about how to register your code.

For questions on access or troubleshooting, please check our FAQs , and if you can''t find the answer there, please contact us .

Oxford University Press

PRINTED FROM OXFORD REFERENCE (www.oxfordreference.com). (c) Copyright Oxford University Press, 2023. All Rights Reserved. Under the terms of the licence agreement, an individual user may print out a PDF of a single entry from a reference work in OR for personal use (for details see Privacy Policy and Legal Notice ).

date: 07 September 2024

Cookie Policy
Privacy Policy
Legal Notice
Accessibility
[66.249.64.20|185.80.150.64]
185.80.150.64

Character limit 500 /500

IMAGES

What Are Causal Loops and How Can We Fix Time Travel?
PPT
Causal Loops in Time Travel
Theory of Time Travel : Causal Loop
What Are Causal Loops and How Can We Fix Time Travel?
Causal loop diagram: feedback mechanism that structurally explains

VIDEO

CAUSAL NEXUS
Frequency (TV Series)
Colorful stalls at #sangamprayagraj on #sunday
TimeTunnel
Chrono Break Openning
The casual loop paradox

COMMENTS

The Myth Of Time Travel
The Myth Of Time Travel ... To do this, the woman-machine complex has to break with the causal nexus it is embedded in before departure. This follows from the fact that it is going backwards in time, while the rest of the universe is moving forward in time. The only way to avoid this rupture would be for everything else to come along for the ride.
Causal nexus
A causal nexus, (TV: Logopolis) also called a spatio-temporal causal nexus point (AUDIO: The Mutant Phase), time-space nexus, temporal nexus point, causal nexus point, nexus point, or just nexus, was a place in space and time that was malleable, (PROSE: Remembrance of the Daleks) points in the space-time continuum that were very rare and hard to access. (PROSE: Invasion of the Cat-People ...
Temporal paradox
A temporal paradox, time paradox, or time travel paradox, is a paradox, an apparent contradiction, or logical contradiction associated with the idea of time travel or other foreknowledge of the future. While the notion of time travel to the future complies with the current understanding of physics via relativistic time dilation, temporal paradoxes arise from circumstances involving ...
Time Travel
Time Travel. First published Thu Nov 14, 2013; substantive revision Fri Mar 22, 2024. There is an extensive literature on time travel in both philosophy and physics. Part of the great interest of the topic stems from the fact that reasons have been given both for thinking that time travel is physically possible—and for thinking that it is ...
Causal Paradoxes
The causal paradoxes of time travel revolve around two related concepts: causal loops and backward causation. This section introduces these ideas in a preliminary way. 1.1 Causal loops. A causal loop is a sequence of events in which each member is a cause of its successor, ...
Causal nexus
causal nexus. (Latin, nectere, to bind)The bonding or link between a cause and its effect. The ancient sceptics, subsequent occasionalists, and, most famously, Hume argue that no such link is perceptible or imaginable: we can see that events do follow one upon another, but we cannot see that they must do so, or frame any notion of the necessary ...
What did Wittgenstein mean by saying that the belief in the causal
In the Tractatus Logico-Philosophicus, Wittenstein says:. 5.1361 The events of the future cannot be inferred from those of the present.. Superstition is the belief in the causal nexus. I'm not quite sure what is meant by "superstition" in this case. Does he mean that if something has happened in the past or in the now, that that is not good enough to assume it will happen again?
Causal nexus
A causal nexus, (TV: Logopolis) also called a spatio-temporal causal nexus point (AUDIO: The Mutant Phase), time-space nexus, temporal nexus point, causal nexus point, nexus point, or just nexus, was a place in space and time that was malleable, (PROSE: Remembrance of the Daleks) points in the space-time continuum that were very rare and hard to access. (PROSE: Invasion of the Cat-People)
Causal Loops in Time Travel
Berkovitz (Berkovitz 2001) and Dowe (Dowe 2001) argue that Mellor fails to establish the impossibility of causality loops. The causal loops in backwards time travel involve events that appear to "come from nowhere," (Smith 2016) paradoxical "self-existent" objects or information, resulting in a bootstrap paradox.
PDF Does Lewis' Theory of Causation Permit Time Travel?
persistence. Since two stages of a time traveler need to be connected by appropriate causal connections in order for the two stages to be part of the one person, and hence to be a time traveler, "... travel into the past necessarily involves reversed causation" [3] (p. 147). In
The Case for Time Travel
A full stomach causes nourish- ment, earlier perceptions are the cause of later memories, and so on. Time travel is where a causal process connects two times in a special way. Dr Who's body is a causal process, and when the Tardis takes him from 1976 to 1876 that causal process connects two times in a special way.
Introduction
Abstract. Chapter 1 explains the concept of time travel, clarifies the main question to be addressed, and previews the paradoxes to come. Section 1 explains the traditional view of time travel as involving a discrepancy between "personal" and "external" time. Section 2 contrasts this kind of time travel with other, purported examples of ...
5 Bizarre Paradoxes Of Time Travel Explained
1: Predestination Paradox. A Predestination Paradox occurs when the actions of a person traveling back in time become part of past events, and may ultimately cause the event he is trying to prevent to take place. The result is a 'temporal causality loop' in which Event 1 in the past influences Event 2 in the future (time travel to the past ...
The Metaphysical Possibility of Time Travel Fictions
Using a time machine, they travel back to 1893, but this time in a Ludovician manner—that is, they time travel back within the same hyperinstant. There, Data loses his head. Since that takes place at the same hyperinstant, the head can later be discovered by the crew at t 2369 - T 3 , creating the causal loop depicted in 'Time's Arrow'.
Backward Causation
The difference, however, is that time travel involves a causal loop whereas backward causation does not. Causal loops for their part can only occur in a universe in which one has closed time-like curves. In contrast, backward causation may take place in a world where there are no such closed time-like curves. In other words, an ordinary system ...
Retrocausality Is the Key to Time Travel. What the Hell Is ...
It's also the key to explaining how time travel, under the laws of quantum physics, could operate. Retrocausality, or reverse causality, is the idea that an effect can happen before its cause ...
What Are Causal Loops and How Can We Fix Time Travel?
Action Causal Loops. To be clear, not all time traveling creates equally perplexing causal loops, or when an action eventually leads back to creating itself (if a then b, b then c, c then a—as an example). If we are closed, then each action leads to only one effect, and so we can follow the loop as a singular path back into itself like a ...
Causal Loops in Time Travel by Nicolae Sfetcu
Abstract. About the possibility of time traveling based on several specialized works, including those of Nicholas J. J. Smith ("Time Travel"), William Grey ("Troubles with Time Travel"), Ulrich Meyer ("Explaining causal loops"), Simon Keller and Michael Nelson ("Presentists should believe in time-travel"), Frank Arntzenius and Tim Maudlin ("Time Travel and Modern Physics"), and ...
[PDF] Causal Loops in Time Travel
About the possibility of time traveling based on several specialized works, including those of Nicholas J. J. Smith ("Time Travel"), William Grey ("Troubles with Time Travel"), Ulrich Meyer ("Explaining causal loops"), Simon Keller and Michael Nelson ("Presentists should believe in time-travel"), Frank Arntzenius and Tim Maudlin ("Time Travel and Modern Physics"), and David Lewis ...
(PDF) Causal Loops in Time Travel
Sfetcu, Nicolae, " Causal loops in time travels", MultiMedia (February 9, 2019), MultiMedia
Time Travel Without Causal Loops
Abstract. It has sometimes been suggested that backwards time travel always incurs causal loops. I show that this is mistaken, by describing worlds where backwards time travel occurs and yet no causal loops occur. Arguments that backwards time travel can occur without causal loops have been given before in the literature, but I show that those ...
Causal nexus
Publisher: Oxford University Press Print Publication Date: 2016 Print ISBN-13: 9780198735304 Published online: 2016 Current Online Version: 2016 eISBN: 9780191799556
Causal Loop version of time travel in Endgame : r/MCUTheories
Time travel indeed happens on a causal loop, but there is an exception to the rule. If you remove a stone during time travel without replacing it you will create a branch reality.. which is what happened with Loki and the Tesseract. Loki escaping with the tesseract and the cap vs cap fight were the only things that weren't suppose to happen.

Tallis in Wonderland

Unrelative Dimensions

Causal nexus

In time [ ]

In space [ ]

In both [ ]

Outside time and space [ ]

Behind the scenes [ ]

Not logged in

Causal nexus

Page actions

Nature [ [edit] | [edit source] ]

Time [ [edit] | [edit source] ]

Space [ [edit] | [edit source] ]

Time and space [ [edit] | [edit source] ]

History [ [edit] | [edit source] ]

War era [ [edit] | [edit source] ]

Post-War era [ [edit] | [edit source] ]

In space [ [edit] | [edit source] ]

In both [ [edit] | [edit source] ]

Outside time and space [ [edit] | [edit source] ]

Behind the scenes [ [edit] | [edit source] ]

Topical pages

Other useful pages

User page tools

Hidden category

5 Bizarre Paradoxes Of Time Travel Explained

Types of Temporal Paradoxes

1: Predestination Paradox

– Cinema Treatment

2: Bootstrap Paradox

3: Grandfather Paradox

4: Let’s Kill Hitler Paradox

5: Polchinski’s Paradox

Are Self-Fulfilling Prophecies Paradoxes?

Are Time Paradoxes Inevitable?

Related Posts

The Metaphysical Possibility of Time Travel Fictions

Cite this article

Similar content being viewed by others

Vacillating time: a metaphysics for time travel and Geachianism

Norton’s Objective Temporal Passage

1 Introduction

2 Ludovician Time Travel

2.2 Ludovician Probability

2.3 Probability and Fiction

3 Non-Ludovician Time Travel

3.2 Universe and Hypertemporal Indexing

3.3 In Favour of Understanding Fiction in Hypertemporal Terms

4 The Mixed Model

5 Fixed Points

5.2 Fixed Points and Ludovician Probability

6 Extensions of the Programme

Acknowledgements

Author information

Corresponding author

Additional information

Rights and permissions

About this article

Share this article

Bibliography

Backward Causation

2.1 Time and Backward Causation

2.3 Distinguishing Cause from Effect

3.1 The Bootstrap Paradoxes

2. Philosophy

2.2 Affecting the Past?

2.5 Free will

3. Paradoxes

4.4.1 Boundary Conditions

4.4.2 Nomic conditions

Acknowledgments

Support SEP

Retrocausality Is the Key to Time Travel. What the Hell Is Retrocausality?

Article Contents

Time Travel Without Causal Loops

Email alerts

Affiliations

This Feature Is Available To Subscribers Only

Recently viewed (0)